I S K O

1. Introduction

After a long period of decline, ontology is back at the forefront of philosophy, science and technology. These days ontology comes in at least two main fashions: the traditional philosophical understanding of ontology has been recently flanked by a new — computer-based — understanding of ontology.

Besides points of contact between the two, there are also a number of differences, perhaps most notably the fact that ontology in knowledge engineering is a discipline still in its infancy, while ontology in philosophy is as old as philosophy itself. Consequently, the history of philosophy contains ideas, tools and proposals of use for contemporary developments; and it also indicates the options that will lead us into dead ends or nowhere at all. When things are viewed in the light of such a long and articulated history, one knows from the outset that ontology does not permit ingenuous simplifications. For these reasons, philosophical ontology may usefully contribute to ontology in knowledge engineering and to ontologies meant as → knowledge organization systems (KOS). (An article on Ontology as KOS is in preparation for this encyclopedia.)

Different authors assign different meanings to ontology and metaphysics. Some use ontology and metaphysics interchangeably (most analytic philosophers, Heidegger), others claim that ontology is broader than metaphysics (Meinong, Ingarden), still others that metaphysics is broader than ontology (most traditional philosophers, Hartmann). Furthermore, the reasons for which one may be broader than the other vary. Before any substantial analysis of the field, therefore, a working delimitation of its range is required. To cut a complex story short, I shall propose the following interpretation:

1. Ontology deals with what, at least in principle, can be categorized (objectified, i.e. subsumed under distinguishable categories).
2. Metaphysics deals with the problem of the totality; generally speaking, there is no way to exclude that the totality could present aspects that we may forever be unable to rationalize, i.e. submit to a rational analysis.

Summarizing briefly: ontology deals with what can be rationally understood, at least partially. According to this interpretation, science in all of its branches is the most successful and powerful ally of ontology. Metaphysics is broader than ontology in the sense that the possibility is admitted of aspects of reality that in principle may go beyond the capacity of any rational enterprise we may happen to develop. Finally, ontics can be thought of as existential ontology, that is, the section of ontology dealing with actual existents.

The distinction between ontology and metaphysics becomes even clearer if one makes reference to the Aristotelian idea of science, according to which there are many different sciences, characterized by specific (types of) objects and their laws: physics is the field of natural movements and transformations, logic the study of (formal) reasoning, politics the analysis of public virtues; rhetoric the study of how to convince others (advertising being its modern facet). Three key questions arise naturally from this perspective point: (1) the categorial structure characterizing each and every science; (2) the mutual connections and forms of dependence and autonomy among sciences; (3) the nature and sense of the whole emerging from them all. The former two questions contribute to defining domain and general ontology, whereas the latter question merges into metaphysics.

[top of entry]

2. Three configurations of ontology

The unity and the variety of the world is the outcome of the complex interweaving of dependence and inter-dependence connections and various forms of autonomy among the many items [2] of which the world is composed. We shall seek to explain the features of this multiplicity by beginning with an apparently trivial question: what is there in the world?

One may say that there are material things, plants and animals, as well as the products of the activities and activities of animals and humans in the world. This first, almost trivial, list already indicates that the world comprises not only things, animate or inanimate, but also activities and processes and the products that derive from them. It is likewise difficult to deny that there are thoughts, sensations and decisions, and the entire spectrum of mental activities. Just as one is compelled to admit that there are laws and rules, languages, societies and customs. We can set about organizing this list of objects by saying that there are independent items that may be real (mountains, flowers, animals, and tables), or ideal (sets, propositions, values), and dependent items which in turn may be real (colors, kisses, handshakes and falls) or ideal (formal properties and relations).

All these are in various respects items that are. Some of the real ones are actually exemplified in the world in which we live; others have been exemplified in the past; and yet others will possibly be exemplified in the future. All real items are therefore temporal items. On the other hand, ideal or abstract items are atemporal, i.e. their form of existence is independent of time (Poli 2001b, chap. 5) [3].

Descriptive ontology concerns the collection of such prima facie information on types of items either in some specific domain of analysis or in general. Formal ontology distills, filters, codifies and organizes the results of descriptive ontology (in either its local or global setting). According to this interpretation, formal ontology is formal in the sense used by Husserl in his Logical Investigations. Being “formal” in such a sense therefore means dealing with categories like thing, process, matter, form, whole, part, and number. These are pure categories that characterize aspects or types of reality and still have nothing to do with the use of any specific formalism.

Formal codification in the strict sense is undertaken at the third level of theory construction, that of formalized ontology. The task here is to find the proper formal codification for the constructs descriptively acquired and categorized in the way just indicated. The level of formalized constructions also relates to evaluation of the adequacy (expressive, computational, cognitive) of the various formalisms, and to the problem of their reciprocal translations.

The close similarity between the terms formal and formalized is somewhat unfortunate. One way to avoid the clash is to use categorial instead of “formal” [4]. Most contemporary research on methodology in ontology recognizes only two levels of work in ontology and often merges the level of the formal categories either with that of descriptive or with that of formalized analysis. As a consequence, the specific relevance of categorial analyses is too often neglected.

The three configurations of ontology differ from each other but there are multiple dependencies among them. Descriptive findings may bear on formal categories; formalized outcomes may bear on their categorial classification, etc. To set out the differences and the connections between the various ontological levels of theory construction precisely is a most delicate but significant task (Poli 2003).

So far we have simply tried to prima facie clarify and delimit the concept of ontology from the related concepts of ontics and metaphysics. Before presenting ontology from the point of view of its contents, two more clarifications are needed.

[top of entry]

3. Ontological presentations

The distinction is needed between pure ontology and its presentations. The latter are related to some point of view (which could be linguistic, cultural or whatever), while pure ontology is independent of the perspectives on it. Otherwise stated, pure ontology is that structural invariant that unifies and underlies all its possible perspective-based variants (ontology as seen from nowhere, as Leibniz would have said). To provide but a sketchy example, a pure ontology may claim that “process” and “object” [5] are the only categories needed and that these are further specified in terms of the distinction, say, between countable and non-countable items [6]. However, for those that are accustomed to the said distinction, a framework offering the possibility to distinguish between countable and uncountable items may prove to be cognitively more transparent and in the end easier to use than a system without it. Ontological presentations are specific settings of the underlying ontological framework intended to better meet the requirements of a community of users.

Unfortunately, it seems that a great deal of the recent ontological work has been conducted in such a way that a specific presentation of ontology (usually in the form of a linguistically-based and furthermore English-based presentation) has been taken as playing the role of pure ontology.

[top of entry]

4. Ontology vs. epistemology

Defining the tasks and characteristics of ontology is also important if we are to avoid confusion with epistemology. The difference can be evidenced by listing concepts of ontology and epistemology. Ontological concepts are: object, process, event, whole, part, determination, dependency, composition, etc. Epistemological concepts are: belief, truth, probability, confirmation, knowledge and all its subsequent modulations (uncertain knowledge, wrong knowledge, etc.).

If ontology is the theory of (the structures of) items, epistemology is the theory of the different kinds of knowledge and the ways in which it is used. The mutual or bilateral form of dependence linking ontology and epistemology does not oblige us to conclude that we cannot represent their specific properties and characteristics separately. On the contrary, we should specify both what ontology can say about epistemology (a belief is a kind of item, it has parts and determinations, etc.), and what epistemology can say about ontology (knowledge of items is a kind of knowledge). This is a difficult task and mistakes are always possible, but there is no principled reason for denying its realizability, even if one understands why it is so easy to blur ontological and epistemological issues.

The ontological and epistemological perspectives interweave and condition each other in complex ways. They are not easily separable, amongst other things because they are complementary to each other.

A further difference — similar but not identical to that between ontology and epistemology — is the difference between an ontological reading and an epistemological one. Consider the sentence:

(1) Napoleon was the first emperor of France.

(2) Somebody was the first something somewhere,

(3) A is/past the first B of C.

From a cognitive point of view, 1 may mean for instance that

(4) The man portrayed by David in the likeness of a Roman Caesar was the first emperor of France (Ushenko 1958).

Neither 2 nor 3 imply 4, whereas 4 does imply 2 or even 3. In general, it is always possible to develop many different cognitive readings of the same sentence. These various readings depend on the information that is implicitly or explicitly added. If we do not add new information, reading 4 above is unjustified because the sentence 1 does not entail the information that Napoleon was portrayed by David.

In general, 2 and 3 (the formal readings) are too poor; they are general but they say too little [7]. On the other hand, 4 is too strong, it is not sufficiently general and it depends on added information. The real difficulty for the ontological reading is that it lies somewhere in between. It is more than the purely logical reading and it is less than the many different cognitive integrations.

The truly ontological viewpoint manifests the many facets of the item. It says not only that somebody was the first something somewhere, but that he performed an important institutional role in some specific part of Europe. It says, moreover, that he was a human being and for this reason that he had a body and a mind, that he was alive, etc.

There is a myriad of information embedded in the sentence “Napoleon was the first emperor of France”. The ontological reading should be able to extract and organize this information without resorting to any external source of knowledge (Poli 2001b).

After these preliminaries, it is now time to present ontology from the point of view of its contents.

[top of entry]

5. Ontology as theory of categories

Following the path opened by such thinkers like Husserl, Hartmann, Peirce and Whitehead (and first of all by Aristotle), ontology adopts a categorial framework.

Resorting to a categorial framework means looking for “what is universal” (either in general or in some specific domain). Those with a grounding in contemporary mathematics will also recognize here the similar claim advanced by Bill Lawvere some decades ago: the theory of category, as a foundational theory for mathematics, is based on “what is universal in mathematics” (Lawvere 1969, 281). Ontology searches everywhere for what is universal. This is precisely the meaning of ontology viewed as a theory of categories.

However, categories come in different guises. Some are taxonomic (is-a, or subclass relation) categories, others are prototypical and there may be other frameworks as well. Moreover, there is also no denying that there are many different types of domain categories (mathematical, linguistic, biological, economic, etc). However, since Aristotle ontological categories are broader than any type of domain categories and deal with the most universal distinctions, starting from the one between substance and accident:

[list added:]

• substance
• quantity
• quality
• relative
• place
• time
• position
• condition
• action
• affection

So understood, most categories are taxonomical categories. A wider perspective point will include not only the classical taxonomical categories we know since Aristotle, but also principles. To remain within a broadly Aristotelian framework, principles include the oppositions between matter and form, power and act, part and whole, being and one. Principles are trans-categorial (where category is taken in the restricted, taxonomical sense) in the sense that they run across the various categories.

As soon as we move from Aristotle to our time, such matters become much more tangled. During the past two centuries the philosophical theory of categories has been subjected to at least six major conceptual revolutions, respectively ascribable to Kant, Hegel, Brentano, Husserl, Peirce and Whitehead. Here we cannot assess all of their pros and cons. However it is noteworthy that all them claim that their main problem is the problem of time, i.e. the problem of the dynamical nature of reality.

[top of entry]

6. The main distinction

We shall adopt item as the universal term. All the subsequent distinctions we are going to consider are distinction among items. Item is more general than the traditional concept ens, read as “everything conceivable”, even if for any practical purposes the two may be taken as essentially equivalent [8]. The first distinction after item is between substances and their determinations (traditionally called accidents). Philosophers have struggled for centuries to gain proper understanding of the category substance. As a matter of fact, the history of philosophy is a remarkable repository of the many variations undergone by the category of substance. It has been variously held that substances are not subject to change, are the unknowable sources of our perceptions, come only in pre-established types, etc. However, in the end the Aristotelian theory of substance is still possibly the most intuitive and productive starting point. The original Aristotelian understanding of substance takes it to be “the bearer of accidents”. Within his framework, substance refers to whatever is at least partially existentially autonomous (i.e. non-dependent). In this sense, living beings are the best exemplifications of substances. Notwithstanding the many problems lurking behind the surface of the Aristotelian point of view, it should however be taken for granted that substances are essentially dynamical realities, i.e. that they change. Furthermore, substances present a number of different “compositions”, i.e. they can be seen from different perspective points (matter-form, power-act, part-whole, etc.). It seems fair to acknowledge that Aristotle failed to establish the proper connections among the theory of categories, the role of the principles (the tension between the dynamics of actuality and potency and the principle of the one being the main sources of difficulty), the theory of whole and parts, and the theory of the continuum. In the end, Aristotle decided to subordinate both wholes and continua to the dialectics of actuality and potentiality. He therefore asserted that whenever the whole is actual, its parts can only be potential. Similarly, whenever the continuum is actual its points are potential. And vice versa in both cases. The main ground for his claims was that “no substance is composed of substances” (Metaphysics 1041 a 5). Similarly, no whole is composed of other wholes. Therefore, parts of wholes are not wholes themselves.

Evidently even of the things that are thought to be substances, most are only potencies — both the parts of animals (for none of them exists separately; and when they are separated, then too they exist, all of them, merely as matter) and earth and fire and air; for none of them is a unity, but as it were a mere heap. (Metaphysics, 1040 b 5–9).

The resulting picture has an apparent coherence to it, but the overall structure is highly unstable: as soon as the slightest change is made to the theory of substance, the theory of wholes and parts or the theory of the continua, the entire framework totters. It therefore comes as no surprise to find that Brentano’s (and for that matter Leibniz’s) innovations to the dialectics between continua and their elements on the one hand, and between wholes and their parts on the other, gave rise to a genuinely new vision (Poli 2004).

Some of the constraints adopted by Aristotle can be loosened, obtaining in such a way a more general theory. First of all, there is no need to maintain that substances should be countable (each substance being a one). Furthermore, not only could it be accepted that substances can be made of other substances, and wholes of other wholes, but it is also possible to admit that accidents may have accidents. This amounts to claiming that substances are not the only things that have accidents; some accidents can be bearers of other accidents. In so doing, beside the substanceaccident tie, also the substance-substance and the accident-accident ties should be incorporated within the framework of general ontology.

A further generalization, foreseen by Brentano, is provided by the idea of substances without accidents. For Brentano, “bodies are […] substances which are not known to have accidents”. The idea that bodies do not have accidents is striking. Either Brentano is utterly wrong or our commonsensical ideas of substance and accident are in need of deep revision.

The apparent strangeness of this position fades as soon as one realizes that accidents can be viewed as referring to the results of measuring processes, i.e. as the modifications suffered by an observing system when it is coupled to an observed system. In this sense not only are rods measuring devices, but also seeing and hearing can be taken as such. What is accidental from the point of view of the observing system may and usually is substantial from the point of view of the observed system. Summing up what we have seen so far, one can sensibly claim that from the point of view of a modernized Aristotelian viewpoint there is no reason to claim that substances must be countable, or possess accidents.

[top of entry]

7. The articulation of substance

Substances can be seen from a number of different frameworks (and requires all them). It may be claimed that one of the reasons for the still unfinished state of the theory of substance is the unsupported oversimplified theory adopted by most philosophers. Our claim is that to properly understand substance we need at least six different theories, five directly dealing with its internal configuration and one dealing with both internal and external aspects. For reasons that will become immediately apparent, we will organize the six theories into three groups: (1) ground categories; (2) universal theories, and (3) levels of reality.

[top of entry]

7.1 Ground categories

The information treated in this chapter of the theory of substance concerns the differences among such general categories as object, process, event, state of affairs, stuff, group, and so on. A widely adopted distinction here is between countable and uncountable natures. Some of the above categories are either countable (object, state of affairs) or uncountable (stuff), some other come in both guises (some processes are countable, others uncountable; cf. Seibt 2004) [9].

[top of entry]

7.2 Universal theories

The instances of ground categories can be further categorized according to a number of different dimensions of analysis. Every dimension of analysis is based on a governing relation. As far as general ontology is concerned, it is important that universal theories avoid any form of domain-based bias.

[top of entry]

7.2.1 Classification

For any kind of item, its instances can be classified. Taxonomies (class-subclass relations or is-a trees, plus instance-of relations) are the best-known forms of → classification [10]. Occasionally other types of classification different from is-a classifications are proposed, e.g. the classification of chemical elements or prototypical classifications. However, these latter forms of classification cannot be included in the section of universal classifications because they are based on specific domain biases: structural information for chemical elements and cognitive saliencies for prototypical classifications.

[top of entry]

7.2.2 Structure

Structure concerns the (1) constitution and the (2) part-whole organization of substances. Constitution is the relation linking a substance to its underlying matter or material. Part-of (in any of its equivalent formal alternatives) provides information about the organization of the item under analysis. Different types of holons (wholes) [11] and parts can be distinguished. I only point out that the classification of holons should distinguish at least among aggregates, wholes in the proper sense, and systems. Aggregates are defined by any appropriate measure of proximity among their parts (e.g. in the forms of similarity or contiguity); wholes require that their parts be linked by some form or other of solidarity (“they move together”, as Aristotle said) [12]; systems, finally, are dynamical wholes. Unity by solidarity is stronger than unity by proximity, and dynamic integration, i.e., formation of a dynamic whole is stronger than unity by solidarity and proximity. This means that only some aggregates are also wholes, and that only some of the latter may be systems. Similarly, different types of parts can be distinguished. Here I mention only parts in the sense of constituent parts (what something is made of) and parts as descriptive parts of the whole. As far as organisms are concerned, organs and their cells are constituent parts of the organism, while, say, hands, arms and trunk are descriptive parts. These two different types of part may or may not coincide. Furthermore, analysis by parts as constituent parts may or may not coincide with analysis conducted in terms of the constitution relation. In order to systematically distinguish the different cases, the theory of levels of reality is required [13].

[top of entry]

7.2.3 Chronotopoids

Drawing on Brentano, I shall treat the general problem of space and time as a problem of chrono-topoids (understood jointly, or separated into chronoids and topoids) [14]. Space and/or time are customarily understood in the form of physical space-time. As necessary as it may be, the physical understanding of spacetime is only one of the many types of ontological spatio-temporal frameworks. Chronotopoids are the most general spatio-temporal frameworks, independently of any material, psychological and social bias.

Development of the theory will require solution of some significant problems. The first of them is establishing which families of chrono-topoids are continuous and which are discrete. The second problem concerns the cohesion of their structure — the forces, that is, which hold them together. In formal terms, this is the same problem as before: devising a theory of, say, the continuum requires knowing how it is constituted. But in ontological terms it is not the same thing. If the continuum is not only a formal structure but also as real one, there must by something (forces?) holding it together. The solution to this aspect of the question relates to the problem of causal connections (see Section 7.2.4 below). Here we find a first interaction between the theory of causes and the theory of chronotopoids.

Much more needs to be added, for something is still lacking from our framework. I shall return to chronotopoids in Section 7.4 below.

[top of entry]

7.2.4 Interactions (causations)

Interactions are forms of causation. Whatever items are recognized by an ontology, they act upon one another and influence one another. For the time being, as in the previous section, I am obliged to confine myself to this rather minimal description of interaction. I shall resume discussion of interaction in Section 7.4 below, after I have introduced the theory of levels of reality.

[top of entry]

7.3 Levels of reality

No general consensus exists about how to define, describe or even sketch the idea of → level of reality. Not surprisingly, my choice is to adopt a categorial criterion: the levels of reality are characterized (and therefore distinguished) by their categories. The main subsequent distinction is between universal categories (those that pertain to reality in its entirety — ground categories and universal frameworks of analysis) and categories that pertain solely to one or some levels of reality.

Most authors prefer instead to adopt an objectual standpoint, rather than a categorial one. Arguing in favor of the objectual standpoint has the undoubted advantage that it yields an elementary definition of level: a level consists of a collection of units. From this point of view, the series of levels is a series of objects interacting at different degrees of granularity. A model of this kind is accepted by large part of the scientific community, because it depicts the widely held view of levels based on a reductionist approach. Higher-order groups of items may behave differently, even to the point that it is impossible to calculate (predict) their specific behaviour, but in the end what matters is that they can all be reduced to the lower atoms.

If this were indeed the way matters stand, then the general neglect shown towards the problem of the levels would be justified. In order to deal with the real complexity of the problem of the levels, the general picture must be altered so that it becomes possible to study not only linear hierarchies but tangled ones as well. This conclusion bears out the approach which undertakes categorial analysis, compared to the one which studies items in iteration. An argument in favor of the approach by objects is the ease with which it is possible to pass from a object-based description to a process-based one: if a level is defined by items in iteration (where the items can be canonically conceived as objects), then a level can be characterized by a dynamic. A multiplicity of structurally stable dynamics, at diverse levels of granularity, may articulate a multiplicity of levels. However, if it turns out that the structuring in levels does not respect a universal principle of linearity, then one is forced to restrict the multidynamic frames to their linear fragments. Which is precisely the situation of current theories of dynamic systems. On careful consideration, in fact, the predominant opinion is that there is only one multi-dynamic (multi-layered) system: the one described by the natural sciences. Other forms of knowledge are scientific to the extent that they can be located in the progressive series of supraformations (groups of groups of groups of items, each with its specific kinds of interaction). Hence the alternative: a discipline is scientific to the extent that it can be located in the series of aggregation levels — if so it can be more or less easily reduced to the base level — or it cannot be thus located and is consequently not a science: it has no citizenship in the realm of knowledge and is scientifically stateless.

The distinction is widespread among three basic realms or regions (or strata, as I will call them) of reality. Even if the boundaries between them are differently placed, the distinction among the three realms of material, psychological and social phenomena is essentially accepted by most thinkers and scientists. A major source of discussion is whether inanimate and animate beings should be placed in two different realms (this meaning that there are in fact four and not three realms) or within the same realm. The latter option involves the thesis that a phase transition or something similar connects inanimate and animate items.

From a categorial point of view, the problem of how many strata there are can be easily solved. Leaving apart universal categories (those that apply everywhere), two main categorial situations can be distinguished: (a) Types (items) A and B are categorially different because the description (codification or modeling) of one of them requires categories that are not needed by the description (codification or modeling) of the other; (b) Types (items) A and B are categorially different because their description (codification or modeling) requires two entirely different groups of categories. Following Hartmann, I term the two relations respectively as relations of over-forming (Überformung) and building-above (Überbauung) [15]. Strata or realms of reality are connected by building-above relations. That is to say, the main reason for distinguishing as clearly as possible the different strata of reality is that any of them is characterized by the birth of a new categorial series. The group of categories that are needed for analyzing the phenomena of the psychological stratum is essentially different from the group of categories needed for analyzing the social one, which in its turn requires a group of categories different from the one needed for analyzing the material stratum of reality.

Over-forming (the type a form of categorial dependence) is weaker than building-above and it is used for analyzing the internal organization of strata. Each of the three strata of reality has its specific structure. The case of the material stratum is the best known and the least problematic. Suffice it to consider the series atom-molecule-cell-organism (which can be extended at each of its two extremes to include sub-atomic particles and ecological communities, and also internally, as needed). In this case we have a clear example of a series that proceeds by levels of granularity. Compared to the material realm, the psychological and social ones are characterized by an interruption in the material categorial series and by the onset of new series of categories (relative to the psychological and social items). More complex types of over-forming are instantiated by them.

A terminological note may be helpful. I use the term level to refer in general to the levels of reality, restricting the term layer to over-forming relationships, and the term stratum to building-above relationships. I shall eventually use the expressions sub-layer and sub-stratum when analysis requires them. The question now arises as to how the material, psychological and social strata are connected together. The most obvious answer is that they have a linear structure like the one illustrated by the left side of Fig. 1.

On this view, the social realm is founded on the psychological stratum, which in its turn is founded on the material one. Likewise, the material stratum is the bearer of the psychological stratum, which in its turn is the bearer of the social one. The point of view illustrated by the left side of Fig. 1 is part of the received wisdom. However, a different option is possible. Consider the right side of Fig. 1. Material phenomena act as bearers of both psychological and social phenomena. In their turn, psychological and social phenomena reciprocally determine each other.

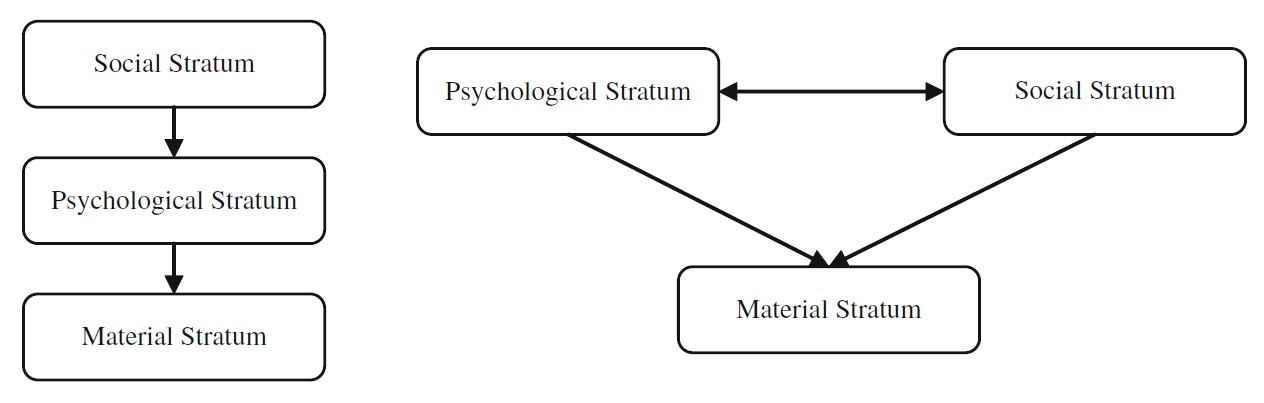
Psychological and social systems are formed through co-evolution, meaning that the one is the environmental prerequisite for the other (Luhmann 1995).

The next step is to articulate the internal organization of each stratum. Analysis shows that the internal organization of the three strata exhibits different patterns [16].

[top of entry]

7.4 Multiplying universal theories by levels of reality

Universal theories provide highly generic frameworks of analysis. It may well be that specific domain ontologies require some appropriate modifications of those generic frameworks of analysis. Indeed, there is no reason to rule out that the general theory of structures (part-of), chronotopoids or interactions to, say, biological items (organisms) or psychological items (representations, or emotions) or to social items (laws, languages, business situations or objects of art) are too general for in-depth analysis of these domain items. The theory of levels comes in here as the main categorial framework for providing guidance on how to proceed systematically with the domain modifications of universal theories.

I am now in the position to add something more to the analysis of chronotopoids and interactions initiated in Sections 7.2.3 and 7.2.4 above.

In the course of the twentieth century, numerous scholars sought to defend and elaborate the idea that there are different kinds of time and different kinds of space. The problem is not just the difference between time as the external order of phenomena (clock or calendar time, understood not only informally but specified up to the desired level of precision) and the inner, subjective time of psychological phenomena (qualitative or phenomenological time). The difference between “time” and “timing” has been described convincingly by van Gelder and Port (1995), and their work may be consulted for a modern version of the difference between the two types of time. I shall not reiterate their arguments here, because the thesis that I wish to discuss is more demanding than that implicit in the difference between the two families of time just mentioned. Stated simply, I shall argue that that there are numerous families of times, each with its own structure. The same applies to space: I shall argue that there are numerous types of real spaces endowed with structures that may differ greatly from each other. The qualifier “real” is essential. I shall not be concerned with the fact — which I consider entirely obvious and not at all disconcerting — that many different abstract (usually mathematical) theories of space and time can be constructed. We shall later need all our mathematical imagination to comprehend the richness of the real; for the time being let us focus on the claim is that there are many real times and spaces.

I have said that during the twentieth century various thinkers sought to defend and elaborate the idea that it is proper to distinguish diverse spaces and times — for example in psychological, social, anthropological, historical, and cultural terms. Unfortunately, it seems correct to say that many of these authors substantially failed in their attempts because they were unable to go beyond allusive and metaphorical renditions of their ideas. The thesis that I propose here is that these failures were due mainly to the lack of a theory of the levels of reality. In the case of the time and space problem as well, we can only hope to move forward by devising an adequately generalized version of the corresponding categories.

To restate, drawing on Brentano, I shall treat the general problem of space and time as a problem of chrono-topoids (understood jointly, or separated into chronoids and topoids).

Development of the theory will require solution to three main problems. The first two have already been mentioned and concern the analysis of (1) which family of chrono-topoids are continuous and which are discrete, and (2) the cohesion of their structure — the forces, that is, which hold them together.

The third problem centers on the synthesis among different chronotopoids. However many the differences may be among the multiple chronotopoids required by the items which constitute reality, chronotopoids do not operate independently of each other; they must merge into a synthetic configuration. In this respect, again, the theory of chronotopoids must obviously rely on a theory of the levels of reality. Some further information may aid the reader in navigating through the complex terrain described. I shall furnish only some basic details. The point to be made most forcefully is that the study of psychological and social phenomena requires a variety of geometric structures (spaces) only some of which are sufficiently known (see e.g. Koenderink and van Doorn 2001). Needed for this purpose are spaces with hierarchical structures (atlases of maps on different scales), spaces with locally unordered structures, point-less continua (whose minimal parts are therefore “infinitesimal”), spaces based on forms of exclusively local organization, and so on. Study will have to be made of multiple relations among these spaces (as well as other types not mentioned). Spaces can be varyingly understood as containers or as structures in which geometric entities are viewed as operators of various kinds. The latter may have inputs, states to be modeled, and corresponding results.

An exemplification which is less abstract and more explicitly tied to the natural articulation of space might comprise the space in which we move, visual space, the visual field, the space of color, various types of parametric space (shapes, phases of movement), and the spaces of meaningful objects (e.g. physiognomies). A large part of the contemporary literature concentrates on structures based on and guided by data, while processual approaches (e.g. of microgenetic type) are very rare (for an exception see Rosenthal 2004). Some of these spaces can be viewed as abstractions of corresponding parametric spaces of physical type (consider the space of colors understood as a three-dimensional subspace of the space of physical radiation), while others have no obvious physical correlate and are apparently authentically mental (hot and cold colors). Of particular interest is the case of pictorial space: that is, the space obtained when an observer looks “into” a painting. Because a painting consists of a surface covered by patches of color in a certain pattern, the pictorial space is a psychic object hallucinated by the observer. Nonetheless, pictorial objects have spatial attitudes, shapes, intrinsic colors and material properties which form a spatial scene. The studies by Koenderink show that pictorial space is a homogeneous space with one isotropic dimension (and is therefore not Euclidean), locally unordered, with a self-similar topological structure.

Passing to interactions, the theory of levels of reality is also the natural setting for elaboration of an articulated theory of the forms of causal dependence. In fact, it smoothly grounds the hypothesis that any ontologically different level has its own type of interactions, or form of causality (or family of forms of causality). Material, psychological and social types of interaction could therefore be distinguished (and compared) in a principled way.

The further distinction between causal dependence/interaction (between items) and categorial dependence (between levels) provides means with which to elaborate a stronger antireductionist vision.

Besides the usual kinds of basic interaction between phenomena of the same nature, the theory of levels enables us to single out upward forms of causality (from the lower level to the upper one). A theory of levels also enables us to address the problem of downward forms of causality (from the upper to the lower level). The point was first advanced by Donald Campbell some years ago (see e.g. his 1974 and 1990). Andersen et al. (2000) collects a series of studies on the theme.

The connection between the theory of levels and causality entails recognition that every level of reality may trigger its own causal chain. This may even be taken as a definition of level of reality: a level of reality is distinguished by its specific form of interactions. As a consequence, we thus have a criterion with which to distinguish among levels of reality and levels of description.

This acknowledgement also enables us to develop a theory able to accommodate different senses of causality (distinguishing at least among material, psychological and social causality). However, if the downward option is also available, the direct or elementary forms of causality should have corresponding non-elementary forms. The theories that are obtained by multiplying universal frameworks of analysis by levels of reality do not pertain to general ontology. By adopting a terminology that has some currency in the field of ontologies as technologies, we may claim that they pertain to core ontologies, i.e. they provide (part of) the interface connecting general to domain ontologies.

[top of entry]

8. Determinations

The two main distinctions within determination are the difference between determinables and determinates and the difference between intensive and extensive determinates. The former distinction is a generalization of the traditional distinction between genera and species, while the basic difference between extensive and intensive determinates is that the former always exist between two points and are based on the relation “more than”, while the latter determinates may be punctiform in nature and are based on “different from” (the following section gives some details on the former distinction).

[top of entry]

9. The substance-determination relation

Both substances and determinations present individual and universal modes. “Socrates” is the expression used to refer to one single individual substance; “philosopher” refers to Socrates, Plato, and Aristotle (and many others besides). “Socrates” is the name of exactly one individual; “philosopher” is the expression for (possibly) many individuals. The same distinction applies to determinations. There are expressions referring to individual determinations (the unique, individual shade of red of this individual object) and expressions referring to possibly many individuals (red). Expressions that can be applied to possibly many individuals are called universals. As we have just seen, the distinction between individuals and universals applies to both substances and determinations. Universals come in levels of generality: “red” is an universal, and “colour” is as well an universal, but obviously “colour” is wider than (more general than) “red”. The same applies to substance-universals: “dog” and “mammal” are both universals, but “mammal” is wider than “dog”. Two different structures arise from this basic framework. Firstly, the connection should be analyzed between individuals and universals pertaining to the same ontological type (i.e. individual and universal substances and individual and universal determinations). It emerges that within each type, the relation linking individual to their universals (to still wider universals) generates a taxonomy (as computer scientists are used to saying, it is an is-a relation: Lassie is-a dog, a dog is-a mammal). Table 1 summarizes these three positions.

Table 1: Three basic positions
 

	Universals are:
	linguistic expressions	concepts	objects
Nominalism	Y	N	N
Conceptualism	Y	Y	N
Realism	Y	Y	Y

Secondly, the relation between substance and determination should be scrutinized. Some of the most demanding traditional problems in ontology arise from the analysis of this problem. The relation between determination and substance is traditionally called inherence (the usual direction goes from determinations to substances: the claim is that a determination inheres in a substance, not vice versa). The problem concerns the ontological nature of universals. In this regard, three main positions are usually distinguished: nominalism, conceptualism and realism (Table 1) [17]. Nominalists claim that universals are linguistic expressions; conceptualists claim that universals result from our cognitive capacities, from our ability to distinguish and categorize our experiences. In this sense universals are concepts. Needless to say, universals as concepts can be named by linguistic expressions; therefore conceptualism seems stronger than nominalism. Realists, finally, claim that universals exist independently of all forms of concrete existence. For the realists, there are both individual and universal objects.

One can then say that nominalists accept only universal expressions, while conceptualists accept both universals expressions and universals concepts, and realists accept universal expressions, universal concepts and universal objects.

[top of entry]

10. From commutative to non-commutative ontology

Ontology has been defined in Section 5 above as the theory of what is universal in reality. This is precisely the reason why ontology adopts the categorial stance. However, one should be aware of the three following problems.

Firstly, general ontology should include such recalcitrant phenomena as those pertaining to the quantum, the emotional and the artistic levels of reality. Not by chance, I have mentioned examples respectively pertaining to the material, the psychological and the social strata of reality. Each of them presents specific forms of complexity, which go well beyond customarily accepted types of complexity. A general ontology intrinsically unable to address any of the mentioned subjects is unsuitable as a true general ontology. According to the proposal outlined above, the theory of levels is the conceptual framework needed to address the over-complex domains mentioned.

Secondly, by their very nature, ontological categories do not admit exceptions. Ontological categories, interpreted as the categories of reality, are essential to their instances. For the reason just given, ontological categories are highly abstract. This is true of both general ontology and domain ontologies (say, biology, or works of arts) [18]. To distinguish the categories of general ontology from the most general categories of any domain ontology, the latter will be called core categories. The framework described by this article explicitly addresses this problem by distinguishing ground categories and universal theories on the one hand, from levels of reality on the other. Levels behave as interfaces that enrich pure universal ontological categories with groups of core categories. On adopting core categories, the ontological framework becomes richer and in this sense more flexible. The theory of levels of reality not only makes this transformation possible but also provides the means with which to avoid ad hoc solutions.

On the other hand — and this is the third issue — as soon as one descends from pure ontological categories (both as general and core categories) to the specific idiosyncrasies of individual instances, the latter may present irreducible features, either as variations or anomalies. Variations can be easily dealt with, because they have a categorial nature. On the other hand, anomalies, or what can be taken as exclusively individual features, are structurally more resistant to categorial analysis.

However, the theory of levels is helpful even for these more difficult cases, because it helps set domain-specific typed forms of differentiation, that is to say, differentiations grounded in the nature of the items composing the level under analysis. As soon as ontological variations and anomalies are recognized (i.e., as soon as reality in its irreducible individuality is recognized) one has therefore moved from an exceptionless categorial framework to a framework admitting variations and anomalies. The theory of levels of reality plays an essential role in both the move from pure universal categories to core categories and from the latter to the variations and anomalies of their instances. Levels are a necessary condition for systematic analysis of these problems. The still unclear issue is the sufficient conditions, if any, for systematically grasp ontological individualities.

The three issues just sketched are only some of the reasons for the shift from a mainly abstract to a properly eidetic (or phenomenological) type of ontology. In this context, “abstract” refers to the extraction of categories by abstraction, i.e., by averaging over instances, while “eidetic” means making explicit the internal nature of any possible item of analysis. The issue is that abstraction can be used only when a collection of items is given [19], while eidetic analysis can be conducted on any single item [20]. Otherwise stated, abstraction is derivative, i.e. secondary, over eidetic analyses.

[top of entry]

11. The interplay between ontology as categorial analysis and ontology as technology

[From Vol. 2 chapter 1, passim]

As we have seen, contemporary ontology can be characterized in a number of ways, all of which can be considered layers of theory: (1) descriptive ontology, concerning the collection of prima facie information either in some specific domain of analysis or in general; (2) formal ontology, which distills, filters, codifies and organizes the results of descriptive ontology; and (3) formalized ontology.

Formal codification in the strict sense is undertaken at this third level of theory construction. The task here is to find the proper formal codification for the constructs descriptively acquired and categorially purified in the way just indicated. The level of formalized constructions also relates to evaluation of the adequacy (expressive, computational, cognitive) of the various formalisms, and to the problem of their reciprocal translations.

In this sense, formalized ontology refers to the actual formalization of ontology in a logical language, typically but not always first order logic (FOL). In ontology as technology, this could be rendered in a knowledge representation language such as the FOL-based ISO Common Logic or in the description logic-based Web Ontology Language OWL.

Ontological engineering, i.e., ontology from the perspective of computer science, has issues comparable to that of philosophical ontology, but reflected technologically in the attempt to develop ontologies as software usable models. So ontology from the perspective of computer science is both a computer science and a computational or software engineering problem. On the one hand, ontological engineering historically had its origins as an engineering problem, as an attempt to create software usable models of “the ways things are, with the things that are” to endow software with human level representations of “conceptualizations” or semantics. On the other hand, there are efforts that intend to make an “ontological science”, as for example, that of the National Center for Ontological Research (NCOR) (Obrst, Hughes and Ray 2006). Such an effort would include strong evaluation criteria and possibly ontology certification. Although having antecedents in the late 1980s, as formal ontology in philosophy and formal semantics in linguistics began to impact computer science and especially artificial intelligence, ontological engineering as a discipline can be marked as originating approximately in 1991, with Neches et al. (1991) reporting on the United States Defense Advanced Research Projects Agency’s (DARPA) Knowledge Sharing Initiative, and Gruber (1991), followed soon after by work by Gruber (1993), Guarino (1994), and Guarino and Poli (1995). […]

Typically, highly general concepts like “process”, “part”, and “boundary” are likely to be included in an upper ontology, while concepts like “gene”, “cell” and “membrane” are likely to be included in a domain ontology for, say, biology. […] Considering biology as a domain with respect to a true upper ontology, then in turn a biology domain ontology may be considered a domain-specific upper ontoogy with respect to many complex sub-domains. These sub-domains can be considered domains in their own right (perhaps also incorporating other domain ontologies, say that of public administration for the case of public health), given the complexity of their subject matter, e.g., mammalian anatomy, neuropathology, genetic engineering, clinical medicine, public health, pharmacology, etc. We might call such a domain-specific UO a middle ontology (that spans multiple domains), a “superdomain” ontology, or simply a domain-specific UO.

[top of entry]

12. Discussion

[Moved to here from Preface] It is true that philosophical ontology addresses questions of a more general nature, ones apparently of no relevance to ontology in knowledge engineering. Consequently, it may appear that certain components of philosophical ontology could be ignored in the passage to ontology as technology. Nevertheless, one should always bear in mind the greater explanatory value and the broader structuring capacity of more general schemes and more comprehensive theories. For this less overt reason, too, philosophical ontology is useful for ontology in knowledge engineering. The philosophical codification of ontology has often restricted itself to organization of its general architecture, without delving into the details of minute categorization. On the other hand, the concrete, situated practice of ontology as technology may conversely prove useful for the development of philosophical ontology.

For these and other reasons, there is mounting interest in the development of standards, modeling principles, and semantically transparent languages. Ontology thus comes into play as one of the strategies available to developing the semantic Web, construct robust data-bases, managing huge amounts of heterogeneous information because ontologically founded knowledge of the objects of the world is able to make codification simpler, more transparent and more natural. The belief is that ontology can give greater robustness to computer-based applications by providing methodological criteria and categories with which to construct and build them, as well as contexts in which to set and re-categorize different data-bases so that they become more mutually transparent. In this way ontology directly contributes to standardization of the life-cycle model, and can therefore serve as an innovative and possibly unexpected component of software quality assurance.

[1.5.5 Final Words]

Ontology as technology needs to be informed by ontology as categorial analysis and its methods. Ontology as categorial analysis will increasingly benefit from the sound and consistent software engineering products arising from ontology as technology. Computer science, formal philosophy, and formal semantics have come together to birth the beasts called “ontology science” and “ontology engineering”. These are strange beasts of Earth but are classifiable and describable under the heavens. Tomorrow it may be that our machines are thereby enabled to in turn be born as stranger beasts, which may yet interact with us human beings as cousins on the well-founded and computationally represented ontological firmament of Earth.

[top of entry]

Endnotes

1. Ion Baianu, Nino Cocchiarella, Claudio Gnoli, Frank Loebe, Leo Obrst, Jerzy Perzanowski, Johanna Seibt, and John Sowa provided comments on preliminary versions of the book chapter used as a basis for this article (see colophon). Section 11 is based on chapter 1 of volume 2 in the same book, written by Roberto Poli and Leo Obrst. Section 12 is based on excerpts from the same chapter and on Poli’s “Preface” to the whole work.

2. On the meaning of “item”, see Section 6 below.

3. Scholars from the Brentanian tradition usually distinguish between existence (for real items) and subsistence (for ideal ones).

4. Note the use of categorial instead of the more usual term categorical. The latter we reserve for the mathematical understanding of category, as for example in topos theory.

5. “Presential”, according to the GFO ontology (GFO stands for General Formal Ontology). Presentials exist entirely at a time-point and are seen as dependent boundaries of processes, which then are the only needed independent category. This section of the GFO ontology is based on Brentano’s idea of time, space and the continuum. See: http://www.ontomed.de/en/publications/scientific-reports/om-report-no8.pdf.

6. See note 9 below.

7. Needless to say, the typed reading is much more informative than the untyped one. However, the ontological problem remains as hard as soon one ask how types are structured and one another connected.

8. To be precise, one should distinguish, together with the Stoics, among soma, on and ti, or with some of the Medievals, notably Gregory of Rimini (1300—1358), among res, ens and aliquid, or again, with Meinong (1853—1920), among real, ideal and Aussersein objects. What is termed soma, res or real object is the body, the on, ens or ideal object is an entity, while the ti, aliquid or Aussersein object is something indeterminate. That which actually exists, the genuine object, is only the soma, res or real object. An entity, by contrast, could well be asomaton or incorporeal. Thus while the soma is subject to the principle of individuation, the on admits at most some criterion of identity, and the ti admits neither identity nor individuation. For them the on can be objective without having to be existent, a soma. On these distinctions see Poli 1996a.

9. However, a deeper analysis may show that the countable-uncountable opposition is either superficial or parochial. It is superficial if the said distinction could be derived from other, deeper categories. On the other hand it may be parochial in the sense that it is a distinction embedded in only some of the world languages. According to Rijkhoff (2002), linguistic data show that six types of nouns can be distinguished: general nouns, sort nouns, mass nouns, set nouns, singular object nouns, and collective nouns. It may also be that the countable-uncountable opposition is both superficial and parochial. Ontological categories run the risk of being parochial when they are grounded on only a section of the available scientific and experiential data. On the other hand, the possible superficiality of ontological categories may depend on cognitive or cultural biases, and in this sense categorial superficiality is a deeper phenomenon; see the section on ontological presentations above.

10. As usual, relying on an already elaborated classification is a different situation from building a new classification.

11. “Holon” was initially used by Koestler (1967). While I endorse his vision, here I am using holon only as a convenient substitute for “whole”, meant as one of the three subtypes of holons.

12. However, Aristotle’s claim is valid only for solids.

13. The main difference being between relations between items pertaining or not pertaining to the same level (either as a stratum or layer) of reality.

14. See Poli (2004) and Albertazzi (2005). Bell (2000; 2005) provide an intuitionistically-based reconstruction of Brentano’s theory. A different interpretation has been elaborated by Baumann, Loebe and Herre (2012). [reference updated]

15. Cfr. Hartmann (1935). The simplified version presented in Hartmann (1952) is worth reading as well. For an introduction to Hartmann cfr. Werkmeister (1990) and the essays collected in Poli (2001d). Even if my vision is substantially different from Hartmann’s, his contribution is a required starting point for anybody interested in the problem of levels of reality.

16. A proper analysis of the social stratum is still awaited. Aspects of my theory of levels have been presented in Poli (1996b; 1998; 2001a–d; 2002; 2006a–b) and in Gnoli and Poli (2004). Caveat: a major misunderstanding of the theory of levels of reality is interpreting the theory of levels as a theory of items’ granularity. That this interpretation is false can be easily seen by considering that the set of physical items comprises both subatomic particles and galaxies and, indeed, the whole physical universe. Physics comprises items at all (real) granularities. Nevertheless physics does not describe all of reality. Something more is required to describe the non-physical aspects of reality, something that, categorially speaking, goes beyond physics, and in two different senses: as a categorial extension of physics (chemistry and biology) and as a categorial alternative to physics and its extensions (the psychological and social strata).

17. As a matter of fact, each of them comes in a number of different guises. The problem is particularly severe for conceptualism, especially as far as the difference between constructive and holistic concept generation is concerned. Realism too can be articulated in different ways. However, in this paper I shall not consider most of these complications.

18. However, different types of domain ontologies should be distinguished, from categorially closed domains to ad-hoc ones. The claim in the main text applies mainly to the former types of domain ontologies. This problem warrants further analysis.

[top of entry]

References