I S K O
Encyclopedia of Knowledge Organization
Mathematics in classification systems
by Craig FraserTable of contents:
1. Introduction
2. Place of mathematics in classification schemes
3. The scope of mathematics in classification schemes
4. The place of calculus/analysis in classification schemes
5. Analysis in the LCC system for mathematics
5.1 Functions of a complex variable
5.2 Complex dynamics
6. Mathematical Reviews and the Mathematics Subject Classification scheme
6.1 Establishment of Mathematical Reviews
6.2 The Mathematics Subject Classification (MSC): 6.2.1 Origins of the MSC; 6.2.2 Mathematics Subject Classification; 6.2.3 The arrival of MathSciNet; 6.2.4 Final reflections on the MSC
Acknowledgments
Endnotes
References
ColophonAbstract:
The modern classification of mathematical subjects occurred within the larger framework of library classification, a project receiving sustained attention in the period from 1870 to the present. The early work of the library cataloguers was carried out against the background of a broad Nineteenth-century interest in the classification of knowledge. We explore different views during this period concerning the position of mathematics in the overall scheme of knowledge, the scope of mathematics, and the internal organization of the different parts of mathematics. We examine how mathematical books were classified, from the most general level down to the level of particular subject areas in analysis. The focus is on the Library of Congress Classification system in its various iterations from 1905 to the present. The article ends with an examination of the Mathematics Subject Classification Scheme employed today by reviewing services Mathematical Reviews in the United States and Zentralblatt in Germany.
1. Introduction
The classification of mathematical studies is involved in extraordinary difficulties, and so is the classifying of many mathematical books. The relations of the branches are so intricate, so plastic, so recondite, that it is well-nigh impossible to define them or to comprehend them.
Henry E. Bliss (1935, 20)
Insofar as → library science is concerned, classification of mathematical subjects occurred within the larger framework of → library classification, a project which has drawn sustained attention from 1870 to the present. The two American giants in library work in the formative period of classification were Melvil Dewey and Charles Cutter. In 1876 Dewey published the famous Dewey decimal system of classification, while Cutter’s Expansive scheme of 1885 would provide the basis for the Library of Congress system. The latter was established in 1905 by James Hanson and Charles Martel, both European immigrants to the United States. In the early Twentieth century additional classification schemes appeared. Among the more notable of these were the “subject” system formulated by the Englishman James Duff Brown and the “bibliographic” system invented by City College of New York librarian Henry E. Bliss.
The practical goal of all classification was information retrieval, allowing for example a user to go to a large library, consult the catalogue, and retrieve a given book of interest. The call number given to a book had to be abstract — it could make no reference to any particular library or to the physical arrangement of the books in any library it happened to belong to [1]. The motivation for classification schemes was the appearance of an increasing number of comprehensive libraries with substantial holdings of books from many subject areas.
Some insight into the classification of books may be gleaned by looking briefly at the question of → classification in the physical world. The pioneering English astronomer William Herschel was interested in the → classification of stellar objects. In an article of 1802 on nebulae and star clusters he announced that he had made something of a breakthrough in connecting the classification of these objects to their inherent characteristics. Herschel (1802, 477) wrote:
The classification adopted in my [earlier] catalogues is little more than an arrangement of the objects for the convenience of the observer and may be compared to the disposition of books in a library, where the different size of the volumes is often more considered than their contents. But here [in 1802] in dividing the different parts of which the sidereal heavens are composed into proper classes, I shall have to examine the nature of the various celestial objects that have been hitherto discovered, in order to arrange them in a manner most comfortable to their construction.
Simon Shaffer (1980, 218) describes this shift in Foucauldian terms as a move from an artificial to a natural system of classification. Of course, the astronomer in his role as natural philosopher is different from the librarian who — as Herschel noted — must take into account physical features or practical necessities related to the handling of books. Furthermore, the classification of books is related to the classification of knowledge, something that is evidently different in character from the classification of objects in the natural world. There is in library classification a tension between epistemological questions related to the organization of knowledge and contingent matters such as collocation, user practice and the storage and retrieval of materials.
Library science, as the discipline of book classification and cataloguing had come to be known by the 1920s, was a subject that integrated the theoretical organization of knowledge with the utilitarian function of identifying and retrieving information. Librarians sought philosophical meaning or justification for the schema they employed, and they appealed to principles of the organization of knowledge. Classification pioneers such as Dewey and Cutter were generalists who were not primarily concerned with any particular subject area. To the extent that their interests were focused on particular fields, these were found in humanistic and social subjects, not in the natural sciences.
Among all of the major systems of book classification, the Library of Congress (LC) Classification scheme was the one that achieved dominance in North American university and research libraries [2]. In 1870 the US Copyright Office was by legislation placed in the Library of Congress, and the Library received copies of all publications submitted for copyright. The holdings of the Library increased and became more complete than any elsewhere, including the collections of major university libraries and large public libraries. This was particularly true for the small-edition research books and monographs in academic fields. In 1901 the Library established its catalogue card distribution service, which allowed libraries throughout America to receive catalogue cards for all published books. Paul Edlund (1976, 398), an historian of the Library, comments on the significance of this development:
By including the card distribution service in its functions, the Library, at that time a reference library to Congress with a small constituency consisting almost exclusively of congressmen and their staff members, was adopting a potentially enormous constituency — that of the total American library community.
The importance of the LCC system in the world of classification was apparent in the years following its establishment. While the major university libraries with their specialized collections containing many older and foreign-language books continued to maintain a patchwork of local classification systems, the LCC has made steady headway up to the present as the dominant and most widely used system of library classification in North America.
The Library of Congress today is also involved in the Dewey decimal system through its Dewey Program. From the website of this Program:
In 1930 the Library of Congress began to print DDC numbers on many of its cards, thus making the system immediately available to the nation’s libraries. Today the Dewey Program continues to support the nation’s libraries, especially public and school libraries, as well as many foreign libraries that classify their collections according to DDC. [3]
Research libraries such as the University of Illinois at Urbana–Champaign that follow the Dewey system adopt call numbers for new books that are provided by the Decimal Program [4]. Through the international use of the Dewey system the LC plays a central role today in library classification not just in the North America but worldwide.
The work of the library cataloguers in the decades around 1900 was carried out against the background of a broad Nineteenth-century interest in the classification of knowledge. In sections one to four we examine how mathematical subjects were classified, from the most general level down to the specific level of particular subject areas in analysis. Section 5 examines in more detail one of these subject areas, complex analysis, and follows the classification of books in this subject up to the present. The final section is devoted to the Mathematics Subject Classification (MSC), developed in the late 1960s by the American Mathematical Society. The MSC applies to both periodical articles and books. A major revision of the system takes place every ten years. With the arrival of the online reviewing services MathSciNet and zbMath, the MSC has become the world-wide accepted standard for classification of mathematical knowledge as we enter the age of electronic publishing.
2. Place of mathematics in classification schemes
Prior to, and concurrent with, the development of library classification systems in the Nineteenth century there was a great deal of interest in the general problem of the classification of knowledge. Although this problem was a venerable one, going back to the Greeks, it was of special concern in the Nineteenth century and was the object of extensive research and discussion of a kind particular to this period. Insofar as the sciences were concerned mathematics occupied a privileged place in this philosophical project. In his book Why Is There Philosophy of Mathematics at All? Ian Hacking explores the prominent place that mathematics has played throughout history in the writings of the great philosophers. In a review of this book Max Siegel (2016, 253) observes that “mathematics has perennially fascinated philosophers, to the point that the philosophy of mathematics is not the philosophy of a special science — like the philosophy of physics or biology — but rather a central field of analytic philosophy.“ In all of the major classification schemes, mathematics is either placed first in a category of general or fundamental science — along with philosophy; or it is put at the beginning of the natural sciences, followed by subjects that follow a presumed reductionist foundational order that exists among them: physics, then chemistry and finally biology.
Although the majority of the thinkers at the end of the Nineteenth century interested in the organization of knowledge were neither scientists nor mathematicians, they possessed definite ideas about the classification of scientific subjects. A recurring theme was the coupling of mathematics with philosophy and its separation from subjects in natural science such as physics, astronomy and chemistry. This point of view seems to have reflected the general and fairly widespread influence of philosophical logicism on contemporary scientific thought.
The Harvard psychologist Hugo Münsterberg was responsible for the scientific plan of The International Congress of Arts and Science held in 1904 at the St. Louis Exposition. Knowledge was divided into seven divisions, and each division was composed of a collection of departments. The divisions were: (A) normative sciences; (B) historical sciences; (C) physical science; (D) mental science; (E) utilitarian science; (F) social regulation and (G) social culture (Brown 1929, 375-380). Philosophy and mathematics comprised division A, while physics and the other traditional natural sciences made up division C.
The philosophical view of the place of mathematics within knowledge never really found favor with librarians who worked on the concrete project of book classification. However, the affinity of mathematics with logic — if not philosophy — and its separation from the natural sciences was a prominent feature of Brown’s 1906 subject classification scheme. Brown held that the classification of books should reflect the classification of knowledge, so that library classification was never a purely contingent project of information retrieval. Brown asserted that logic and mathematics should be grouped together under “Generalia” and should precede all other branches of knowledge, being preliminary to any field of investigation, from physics to economics to philosophy and history, or anything else. Classes of knowledge were given by Brown in the following order: generalia, physical science, biological science, medical science, agriculture and domestic arts, philosophy and religion, social and political science, language and literature, literary forms, and history and geography.
Brown's classification was also distinctive in its positioning of practical subjects adjacent to their presumed theoretical counterparts. Following the section on mathematics there would be books on painting and sculpture. There were two reasons for such an arrangement. First, fine and graphic art exemplified the visual point of view of geometry and could be regarded in some sense as the embodiment of geometric ideas. Second, Brown believed that the subject of visual representation was fundamental in character and that familiarity with it was necessary for its use in various applied fields of investigation and work. It may seem odd that the section of the library stacks devoted to mathematics would be followed by books on Flemish art, while books on physics would be located a few aisles over — but such was Brown's rather idiosyncratic notion of book classification!
A librarian influenced by Brown was Henry Bliss of the City College of New York. More than Brown, Bliss emphasized the affinity of mathematics with philosophy and logic and its separation from science. He wrote two books on the organization of knowledge: the first (1929) was a general and somewhat philosophical work, while the second (1933) was directed more specifically to the classification of books. Bliss regarded mathematics more as a method than a branch of science, and he believed that a grounding in logic was proper preparation for its study. He observed (1929, 258) that “Logic is usually regarded as a branch of philosophy and the close relation of philosophical thought to mathematical thought is often affirmed”. He had many criticisms of the Library of Congress Classification scheme, including the position of mathematics: “In a broader aspect the separation of Sciences in Q from philosophy in B involves such an unscientific and unphilosophic consequence as separating Philosophy of Science from Philosophy of Knowledge, and more generally separating Logic (BC) from Mathematics (QA), despite the claims of both logicians and mathematicians that their studies are inseparable”.
The conception of Münsterberg and Bliss was implicitly rejected by thinkers concerned only with the organization and classification of subjects in the natural sciences. For them, mathematics clearly had to be included as a subject area, usually at the beginning of the classification, while philosophy did not appear at all. Any viable classification scheme would need to reflect the place of subjects in the real world. Classifying mathematics with philosophy and separating it from physics and engineering might be sensible in the domain of humanistic thought, but it made little sense in actual practice.
In the Cutter, Dewey and LC classification schemes mathematics is separated from philosophy and grouped with the natural sciences. In the Dewey system, philosophy is placed near the beginning under 100, and is followed by theology (200), sociology (300), and philology (400). The natural sciences comprise the 500s, with mathematics (510) as the first science subject proper, followed by astronomy (520), physics (530) and chemistry (540).
Cutter also grouped philosophy near the beginning under the letter B, where it was followed by religion and theology (C and D), biography (E), history and geography (F), social sciences (H) and natural sciences and applications (L). The presentation of subjects under L followed the order mathematics, physics, chemistry, and astronomy, with designations via subscripts: mathematics (LB), physics (LH), chemistry (LO) and astronomy (LR). Cutter classified the remaining science categories under the letters M through S: natural history as well as geology and biology (M); botany (N), zoology (O), anthropology and ethnology (P), and medicine (Q).
The LCC system seems to have been patterned after Cutter and the placement of philosophy with respect to the natural sciences follows this earlier system. Sayers (1915-16, 135) observes that “The outline of the [LC] classification is almost directly based upon The Expansive system, as a comparative paradigm of the two will demonstrate”. The LCC will be the subject of more detailed study in sections 4 and 5.
3. Scope of mathematics in classification schemes
Until the Nineteenth century mathematics was interpreted broadly to include subjects that today would be regarded as part of astronomy, physics or engineering. But by the second half of the Nineteenth century, when library classification systems were being developed, the scope of mathematics had narrowed substantially.
Writers such as Münsterberg and Bliss who viewed logic and mathematics as kindred subjects and grouped mathematics with philosophy adhered to a conception of mathematics that certainly did not include subjects in physics such as mechanics. However, these thinkers did not represent scientists and mathematicians themselves. Among the latter mathematics was a subject that involved traditional logic only very peripherally if at all. Discussions of the scope and relative position of purely scientific subjects in the Nineteenth century focused on what was called the hierarchy of sciences, a notion introduced by Auguste Comte in 1830 in the second lesson of his Cours de philosophie positive. Comte believed that there is a natural progression of scientific subjects, beginning with mathematics, passing through astronomy, physics, chemistry and biology, and ending with sociology. This hierarchy could be justified on methodological or philosophical grounds, and was often taken for granted for practical reasons. The Comtean hierarchy of sciences was accepted by virtually all of the systems of book classification, and survives to the present.
Among those writers who were primarily interested in the natural sciences, mathematics was placed within science, at the very beginning of the Comtean hierarchy. An important figure was the French physicist André-Marie Ampère, who along with Comte and some other French figures of the period was a mathematical empiricist in orientation. These authors separated mathematics completely from philosophy, which tended to occupy a lower position in the overall scheme of knowledge and learning than it had traditionally held. Mechanics was a kind of hybrid subject, part of mathematics and different from subjects in physics, but distinct from arithmetic and geometry in possessing a physical character.
Ampère presented a rather detailed and elaborate classification scheme for the sciences in his Essai sur la philosophie des sciences of 1834. The mathematical sciences were made up of arithmetic, geometry, mechanics and astronomy. Arithmetic and geometry were mathematical subjects “proprement dites”, while mechanics and astronomy were physico-mathematical in character. The physical sciences included atomic theory and chemistry.
Ampère’s point of view was reflected in some later French writers on scientific classification. Thus Charles Renouvier (1859) in his Essais de Critique Générale put rational mechanics and applied mathematics together with mathematical subjects (arithmetic, algebra, mathematical analysis, geometry) in the category of Logical Sciences, which were to be distinguished from Physical Sciences, the latter including astronomy. At the end of the century Edwin Goblot’s Essai sur la classification des sciences (1898) positioned mechanics as part of mathematics and distinguished it from physics. The estimable Scottish authority Robert Flint (1904, 278), in his survey of work on classification, seems to regard mechanics as part of mathematics, writing that mechanics “is as abstract as Geometry, and in its applications is not more concrete”, and “Mechanics is both abstract and concrete, both quantitative and qualitative, and cannot be denied to be on the borderland between mathematical and physical science” [5].
Although Ampère’s understanding of the scope of mathematics was adopted by some later authors, the view that came to be much more common as the century progressed was just the opposite. There was a decided shift away from the view that mechanics was part of mathematics. In the last part of the century both humanistic and scientific thinkers interpreted mathematics as a subject more or less co-extensive with what today would be called pure mathematics.
This shift is apparent in the writings of the English polymath Herbert Spencer, who published in 1864 The Classification of the Sciences. Spencer opposed Comte's hierarchy, mainly on the grounds of the reductionist ordering of the sciences along a linear sequence that it implied. Spencer was among that group of thinkers who believed that logic and mathematics were closely connected and distinguished by their abstractness from the natural sciences. Mathematics and logic dealt with relations, while the natural sciences dealt with objects. Rather than putting the natural sciences into a sequence he divided them into two distinct groups: the abstract-concrete sciences, consisting of mechanics, physics and chemistry; and the concrete sciences, consisting of astronomy, geology, biology, psychology and sociology.
The exclusion of mechanics from mathematics was also advocated by the prominent Austrian physicist Ernst Mach, who published his noted critical and historical account of mechanics in 1883. Although Mach’s philosophy shared similarities with the empiricist outlook of Comte and Ampère, he insisted that mechanics was not part of mathematics. At the beginning of the preface to his book he proclaimed:
Mechanics will here be treated, not as a branch of mathematics, but as one of the physical sciences. If the reader's interest is in that side of the subject, if he is curious to know how the principles of mechanics have been ascertained, from what sources they take their origin, and how far they can be regarded as permanent acquisitions, he will find, I hope, in these pages some enlightenment. All this, the positive and physical essence of mechanics, which makes its chief and highest interest for a student of nature, is in existing treatises completely buried and concealed beneath a mass of technical considerations. (Mach 1883, i) [6]
Mach's position was influenced by his phenomenological understanding of mechanics and his belief that a priori metaphysical conceptions had no place in physics, a mistake that could arise if mechanics was taken as part of mathematics. There were also important developments in Nineteenth-century mathematics that influenced scientific thought in the century’s second half. In a footnote toward the end of his book Mach discussed the discovery of non-Euclidean geometry. This discovery showed that geometry was not simply a description of spatial reality, for there were multiple geometries and only one spatial reality. Mathematics including geometry was evidently about intellectual structures, while mechanics was about objects in the external world. Non-Euclidean geometries existed, but non-inertial physics did not. Mach was opposed to the interpretation of the properties of real space (“die Eigenschaften des gegebenen Raumes”) by what he called “the pseudo-theories of geometry that seek to excogitate these properties by metaphysical arguments”.
The common view among the classifiers of science in the second half of the century was that mathematics did not include mechanics. This fact is apparent in a broad range of authors discussed by Flint in his 1904 historical survey. William Whewell in 1858 distinguished mathematics (arithmetic, geometry, algebra, differentials) from astronomy and mechanics (Flint 1904, 198). W. D. Wilson in 1856 separated mechanics, which he called a practical science, from mathematical subjects (arithmetic, algebra, geometry, calculus) which made up, with the study of method and ontology, the pure sciences (Flint 1904, 215–216). Eugène de Roberty in an 1881 book on sociology separated mathematics from mechanics, regarding the latter as a descriptive science (Flint 1904, 263-4). In his 1887 book Versuch einer concreten Logik, the Prague philosopher Tomáš Masaryk advocated a hierarchal conception of science, placing mathematics first and assigning mechanics to a second group (Flint 1904, 277-8) [7]. Masaryk followed Mach in explicitly separating mechanics from mathematics. In 1870 the Scottish philosopher Alexander Bain asserted that mathematics was distinct from mechanics, and placed the latter with physics (Flint 1904, 241-2). In Karl Pearson’s Grammar of Science of 1892 logic and mathematics were classified as abstract sciences, while mechanics was one of the concrete sciences. One year later Raoul de La Grasserie followed Herbert Spencer in classifying mathematics as an abstract science and mechanics as abstract-concrete (Flint 1904, 289-292). Writing in the early 1930s but expressing long-held views, Henry Bliss (1933, 293) asserted that the possibility of a mathematical treatment of mechanics “should not mislead scientists to admit the claims of some mathematicians that Mechanics is merely a branch of Mathematics. That is not true even or Rational, or Analytic Mechanics, which of course should not be dissevered from the sub-science as a whole”.
The book-classification schemes at the end of the century were united in limiting the scope of mathematics, and in either placing mechanics within physics or including it as a subject area in its own right. In Cutter, mechanics was put with physics rather than mathematics, while astronomy was made a distinct subject area, after chemistry. Although Dewey had included some applied subjects in mathematics, mechanics was placed in physics, along with optics, thermodynamics and electromagnetism. In the International Catalogue of Scientific Literature (see Section 4) mechanics received its own subject area, intermediate between mathematics and physics. In the systems of both Brown and Bliss, mechanics is separated from mathematics and classified as a physics subject, along with thermodynamics and electromagnetism.
Alone among the major classification systems, the LCC scheme placed mechanics under mathematics, and situated astronomy as a subject field between mathematics and physics. The title of the original LCC volume on mathematics is worded Class QA: Mathematics (Including Analytic Mechanics). It is not entirely clear why the architects of LCC proceeded this way, but the grouping of mechanics within mathematics is a singular feature of the LC classification system that continues to the present.
4. The place of calculus/analysis in classification schemes for mathematics
Comte's distinction between abstract mathematics consisting of arithmetic, algebra and calculus, on the one hand, and concrete mathematics, consisting of geometry and mechanics on the other, reflected a classificatory order that placed calculus ahead of geometry. It was also in keeping with the prevailing conception in French mathematics of calculus as a form of “algebraic analysis”, the very title of Augustin Cauchy’s famous textbook of 1821 on the calculus.
In his 1834 book Ampère introduced neologisms to designate the various subject areas of mathematics. What he called "arithmologie" was divided into two parts, the first consisting of arithmetic and algebra, and the second consisting of the theory of functions and the theory of probabilities. The theory of functions included calculus-related parts of mathematics. Geometry was the second major subject area of mathematics, under which Ampère placed synthetic and analytic geometry, as well as the theory of lines and surfaces and something called molecular geometry. The other major subject area of mathematics consisted of the physico-mathematical subjects mechanics and astronomy (the latter called “Urinologie” by Ampère). Mechanics in turn was divided into elementary and transcendental mechanics, while astronomy was divided into general astronomy and celestial mechanics.
Among the many writers who wrote on classification of science from the 1840s to the end of the century, the predominant tendency was to depart from Comte and Ampère by placing geometry ahead of calculus. Mathematical subjects were placed in the standard order: arithmetic, algebra, geometry and calculus. Whewell (1858) conceived of mathematics as the subjects “Geometry, Arithmetic, Algebra, and Differentials, and based on the ideas of space, time, number, sign, and limit” (Flint 1904, 199). Bain (1870) divided mathematics into arithmetic, algebra, geometry, algebraic geometry and the higher calculus (the latter dealing with incommensurable magnitudes) (Flint 1904, 199). Wilson (1856) gave the order arithmetic, geometry, algebra, calculus, trigonometry and analytic geometry (Flint 1904, 216). Paul Janet (1897) used abstraction as something that distinguished arithmetic, geometry and mechanics from algebra and the differential and integral calculus (Flint 1904, 304). Flint (1904, p. 278) himself wrote that "Arithmetic and Geometry are very different both as to matter and method from Calculus and Kinematics" [8].
With the exception of the Library of Congress, the major library classification schemes around 1900 placed geometry before calculus. Dewey and Cutter both adopted the order arithmetic, algebra, geometry, trigonometry, and calculus, while Brown presented these subjects in the order arithmetic, algebra, geometry, calculus, and trigonometry. The librarians presumably were guided by historical and pedagogical considerations: calculus had originated as a set of methods for the study of curves and surfaces, and calculus was a more advanced teaching subject than elementary geometry and therefore was placed after it. The librarians may also have perceived the natural order to be one of successive abstraction, and calculus and higher analysis were viewed as more abstract than geometry [9].
Although the focus in this section is on the classification of books, it is necessary to look at how periodical mathematical literature was classified by subject in the second half of the Nineteenth century, as this would bear directly on the classification scheme for mathematical books adopted by the LC. Unlike book classification, which was aimed at a broad readership at various levels of engagement with the subject, the practices followed by journals reflected the outlook of active researchers in the field. Insofar as the ordering of subjects is concerned, the point of view was essentially a continuation of the French outlook expressed by Comte and Ampère early in the century. The Zeitschrift für Mathematik und Physik, founded in 1856, was one of the first journals to explicitly divide its contents into subject categories. The latter were presented in the order arithmetic and analysis, geometry, mechanics, optics, electricity and Galvinism, and smaller and miscellaneous subjects. This selection of topics and their ordering was certainly not pedagogical. Even from the viewpoint of its intended audience it was not an altogether natural ordering. The table of contents was based on an implicit understanding of the logical character of mathematics and the relationships that exists among its parts. The grouping of analysis with arithmetic and its placement ahead of geometry reflected the prevailing view of advanced researchers, and indicated more generally the well-known “arithmetization of analysis” of mathematics in the Nineteenth century. Calculus in its original formulation was known as “fine geometry”, and Eighteenth-century masters of analysis such as Euler and Lagrange were known as geometers. By the second half of the Nineteenth century the research picture had shifted substantially, and geometry had become something of a subsidiary subject with respect to the primary grounding of mathematics in arithmetic, algebra and analysis.
Carl Ohrtmann and Felix Müller were Berlin gymnasium teachers of mathematics who founded in 1871 the reviewing periodical Jahrbuch über die Fortschritte der Mathematik. There was a large increase in the growth of mathematical literature in the Nineteenth century, and a corresponding need to assist researchers in navigating materials published in their fields. Ohrtmann and Muller modelled the Jahrbuch after an abstracting journal for physics that had already been in existence for close to twenty-five years, the Fortschritte der Physik. Although the publications reviewed in the Jahrbuch consisted mainly of periodical literature, books were also included. The Jahrbuch followed Ampère and the Zeitschrift in its presentation of subjects and their ordering: history and philosophy, algebra, number theory, series, differential and integral calculus, function theory (complex functions), pure, elementary and synthetic geometry, analytic geometry, mechanics, mathematical physics (electromagnetism, theory of heat, optics), and geodesy and astronomy [10]. Since there was already a physics reviewing journal, the physics subjects included in the Jahrbuch were ones in which the treatment was highly mathematical.
At the end of the century the Royal Society of London established the International Catalogue of Scientific Literature (1902), a major international bibliographic project that was intended to cover both periodical and book literature. In this work mathematics (which was also referred to as “pure mathematics”) was divided into the following subject areas: fundamental concepts, algebra and number theory, analysis, and geometry. This ordering of subjects became canonical in the classification of Twentieth century mathematical literature, at least as this was followed by the LCC and mathematical reviewing services. (It should be noted that the Dewey system continued to place geometry before calculus and analysis up until the late 1960s, at which time its schedules were revised and brought into alignment with the LC.)
The classification schedules for mathematical subjects in the original LCC system of 1905 were compiled by J. David Thompson, chief of the science section, under the direction of Martel, head of classification for the whole of LC. Thompson was a native of England who had studied mathematics at the University of Cambridge, graduating 16th Wrangle in 1895. In the preface to the volume on science he (1905, 3) states that he has relied notably on the schedules of the International Catalogue of Scientific Literature. While the overall scheme of the LCC system was patterned on the Cutter system of classification, the organization of scientific subjects followed the ICSL. Insofar as advanced mathematical subject areas were concerned, Thompson followed the ICSL very closely. The 1905 edition of the LC science schedules was republished in multiple later editions, each containing modifications and extensions of the original scheme.
In the 1930s there were two new library classification systems, Bliss’s bibliographic classification and S. R. Ranganathan’s (1933) → Colon Classification. Although Bliss presented the three subject areas of mathematics as arithmetic-and-algebra, geometry and analysis, he classified these subjects in the order arithmetic-and-algebra, analysis and geometry. He made this change for reasons of what he called “collocation”, apparently referring to the usage established by the ICSL and the LCC. Ranganathan also classified mathematics subjects in the order arithmetic, algebra, analysis and geometry, and followed LCC in including mechanics within mathematics. In a departure from all other classification schemes he placed astronomy within mathematics.
5. Analysis in the LCC system for mathematics
5.1 Functions of a complex variable
In the LCC system books on science are classified under Q, and those on mathematics are classified under QA. In 1905 some parts of mathematics hardly existed yet as recognized subject areas. In the ICSL under arithmetic there was a subject entry on “aggregates”, what would later be called the theory of sets, but there was no entry at all for this subject in the LCC. When Abraham Fraenkel’s Einleitung in die Mengenlehre appeared in 1919 it was classified in the LC under foundations of arithmetic (QA248) in the algebra section, and that became the standard LCC subject classification for books on set theory.
A part of mathematics that was very well established in 1905 was analysis, and books on this subject received call numbers in the range from QA300 to QA400. The theory of functions was designated QA331 and was made up of books we would regard today as belonging to complex analysis. The theory of functions of a real variable came to be designated QA331.5, being regarded as a branch or offshoot of the theory of functions. The classification scheme is evident in the following two books on analysis from the early years of the century:
QA331Heinrich Burkhard, Theory of functions of a complex variable (1913)QA331.5James Pierpont, Lectures on the theory of functions of real variables (1905-12)
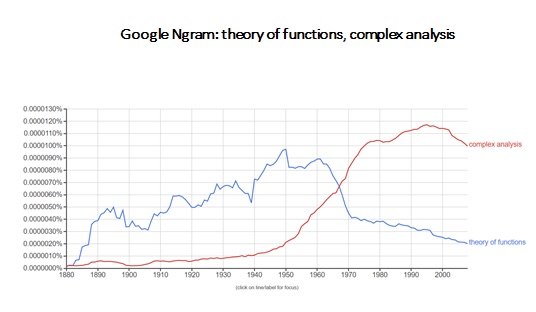
When Lars Ahlfhors’ Complex Analysis was published in 1953 it was given the LCC subject designation QA331. In the 1960s complex analysis replaced the theory of functions as the standard subject name for the theory of functions of a complex variable [11]. At this time, one also began to see the publication of books with the term “real analysis” in the title. H.L. Royden’s Real Analysis appeared in 1963 and was given the subject designation QA331.5. Thus, real analysis was envisaged in this classification scheme as an offshoot of complex analysis. The earlier subject classifications QA331 (theory of functions, implicitly functions of a complex variable) and QA331.5 (theory of functions of a real variable) mapped onto the new subject names complex analysis (QA331) and real analysis (QA331.5).
In the LCC books on analysis with the classification QA300 are devoted to the more general parts of analysis and the foundations of the subject. A widely used primer on analysis for senior undergraduate and graduate students from the 1950s and 1960s was Walter Rudin’s Principles of Analysis (1953 and later editions). Rudin’s book was classified under QA300. We have the classification sequence:
QScience
QAMathematics
QA300Rudin Principles of Analysis
QA331Ahlfors Complex Analysis
QA331.5Royden Real Analysis
By the 1970s some books on real analysis were assigned the designation QA300, and thus were understood to belong to more general parts of analysis, prior in the classification scheme to complex analysis. Other books on real analysis continued to receive the traditional designation QA331.5. There was an overhaul of LC mathematical analysis subject designations in the 1980s, and this change is contained in the current schedule that may be found online (http://www.loc.gov/aba/publications/FreeLCC/Q-text.pdf). The change had been made by around 1990. Here is how the breakdown for subjects in analysis is now given:
Analysis
QA300General works, treatises, and textbooks
Theory of functions
QA331General works, treatises, and advanced textbooks
QA331.3Elementary textbooks
QA331.5Functions of real variables
QA331.7Functions of complex variables
Riemann surfaces including multiform, uniform functions
Evidently the QA331 section dealing with the theory of functions has been reorganized to reflect the standard order of subject presentation: first general works, followed by elementary presentations, and then according to some presumably natural principle, an ordered list of the subject areas that fall under the theory of functions.
An old principle of book classification followed by the LCC that is very useful to the historian is that books are not reclassified when a revision, either major or minor, of the classification system takes place [12]. This seems to be partly for practical reasons — it would be difficult for libraries to be continually reclassifying the materials in their collections. It should be noted that although the classification of a book is not changed, in the LCC a later edition of a given book may have a different call number. For example, Stanley G. Krantz’s Function Theory of Several Complex Variables was classified as QA331 when it appeared in 1982, a designation that remains unchanged to this day, while the second edition of this book in 1992 received the call number QA331.7.
The principle of the organization of scientific subjects which is followed in library catalogues is foundational: more basic subjects come first, followed by progressively more complex subjects. Underlying the conception of foundation is a building metaphor, invoking the structure and construction of a building. A classification where real analysis is placed before complex analysis is consistent with a foundational conception of subject classification. In the original LCC, where functions of a real variable is a sub-subject of the theory of functions, David Thompson was presumably thinking of classification in a somewhat different way, as a division in which the complete subject comes first, and where one proceeds from there to obtain various special subject areas that fall within the general subject. In certain contexts, this second approach to classification may seem more natural or practical, as it would, for example, if one were classifying goods in a department store. To find a given make of coffee maker one would locate the section on household goods, proceed to the section on kitchen supplies, and then find the section on kitchen appliances, ending finally in the section on coffee makers. The conventional ordering of intellectual subjects — at least ones in science — follows a different, foundational principle that is inherent in the epistemological character of the subject matter.
It should be noted that there was also an evolution in the classifications schedules for mathematics employed in the Dewey Decimal Classification. The original Dewey schedule from 1885 for books on mathematics was:
511Arithmetic
512Algebra
513-516Geometry
517Calculus (analysis)
In 1971 the classification schedule Dewey 18 included a reclassification of books in some parts of mathematics. The call number for books on analysis was changed from 517 to 515, while books in geometry that originally would have been classified under 515 were classified as 516. For example, a book on complex analysis published in 1966 was classified under 517, while a book on the same subject in 1972 was classified under 515. In addition, the classifications for arithmetic and algebra were reversed, so that arithmetic became 513 while algebra remained at 512. The current Dewey classification schedule for books in mathematics is:
512Algebra
513Arithmetic
514Topology
515Analysis
516Geometry
The change in the classification brought the Dewey system into conformity with the LCC as well as with the Mathematics Subject Classification system used by reviewing periodicals such as Mathematical Reviews and Zentralblatt [13]. One major research university in North America that uses DDC today is the University of Illinois at Urbana-Champaign. In the 1980s the Mathematics Library received a government educational grant to update the Dewey classification of mathematics books at UIUC, and this included re-marking the books and the shelf list cards in both the Mathematics Library and the Central Book stacks [14]. By contrast the public libraries of Cleveland and Cincinnati have retained the original Dewey classifications for their older books.
Prior to 1971 books on functions of a complex variable and books on functions of a real variable in the Dewey system where both standardly catalogued under the call number 517.5. There was no relative placement of one group with respect to the other, as there was in LCC. When books with complex analysis and real analysis in their titles appeared in the 1950s and early 1960s, they were all given the same call number 517.5. During the later 1960s books on complex analysis were being classified as 517.8, while ones on real analysis continued to receive 517.5. After 1969 or 1970 all books on analysis shifted from 517 to 515, with books on real analysis being assigned 515.8, and ones on complex analysis being assigned 515.9 [15].
5.2 Complex dynamics
A challenge for library classification is the appearance of new subject areas within mathematics, and the question of how to classify the resulting book and monograph literature. This point was addressed briefly above for the case of set theory. An example that illustrates some of the issues involved here is the emergence of complex dynamics in the 1980s and 1990s. This was an area of research whose existence as a mathematical subject was the result of the exponential increase in computational power that accompanied the computer revolution.
The Oxford English Dictionary defines dynamics as the "the branch of mechanics concerned with the motion of bodies under the action of forces". This is how the word is used going back to Jean d'Alembert's classic Traité de Dynamique of 1743. Books on dynamics in this sense are classified by the LCC in the QA800 series, as a broad subject area within mechanics. The OED further defines dynamics as "the branch of any science in which forces or changes are considered". The term dynamical is traditionally associated with change and motion resulting from forces or powers. In jargon-laden modern English it tends to be used in any context to add a formal element to a description of change or flux.
In the early 1970s the subject classification QA614.8 appeared, under the heading of differentiable dynamical systems, a field within the broader subject area QA614 of global analysis. Dynamical systems originated in the early part of the century and focused on the qualitative study of the solutions of the differential equations that arise in the three-body problem and similar problems. Pioneers in this field were Henri Poincaré and George D. Birkhoff. It would be a popular field at the of the Twentieth century and came to include various topics in non-linear analysis, chaos, complex iteration, and fractals [16].
In the 1980s the study of discrete dynamical systems emerged as an active area of mathematical research. A discrete dynamical system consists of a sequence of values obtained through any process of iteration (Devaney 1987, 2-3). An area of research in complex analysis since the late Nineteenth century was the iteration of complex polynomials. The iteration of a polynomial is an example of a discrete dynamical system. In the 1980s this part of mathematics was singled out and given a name, “complex dynamics,” and a new subject area was apparently born. James Gleick in his 1987 Chaos: Making a New Science (p. 227) explained the iteration of complex polynomials in terms of the arithmetic of complex numbers, a conception in which dynamics could not be said to be present even in a metaphorical sense. Nevertheless, the way in which the given polynomial moves around under iteration in the complex plane and seems in certain cases to be attracted to or repelled from fixed points has a dynamical feel, as this word has come to be used in English. Computer-aided computation somewhat unexpectedly opened up a whole new range of phenomena within a traditional part of mathematics.
The term complex dynamics appears in the title of an article by the American mathematician Paul Blanchard in 1987, “Complex analytic dynamics on the Riemann sphere”. The first book with the term in its title was Lennart Carleson and Theodore W. Gamelin's 1993 Complex Dynamics. The Google Ngram for "complex dynamics" (Figure 2) indicates how suddenly it emerged as a subject area of mathematics at the end of the century.
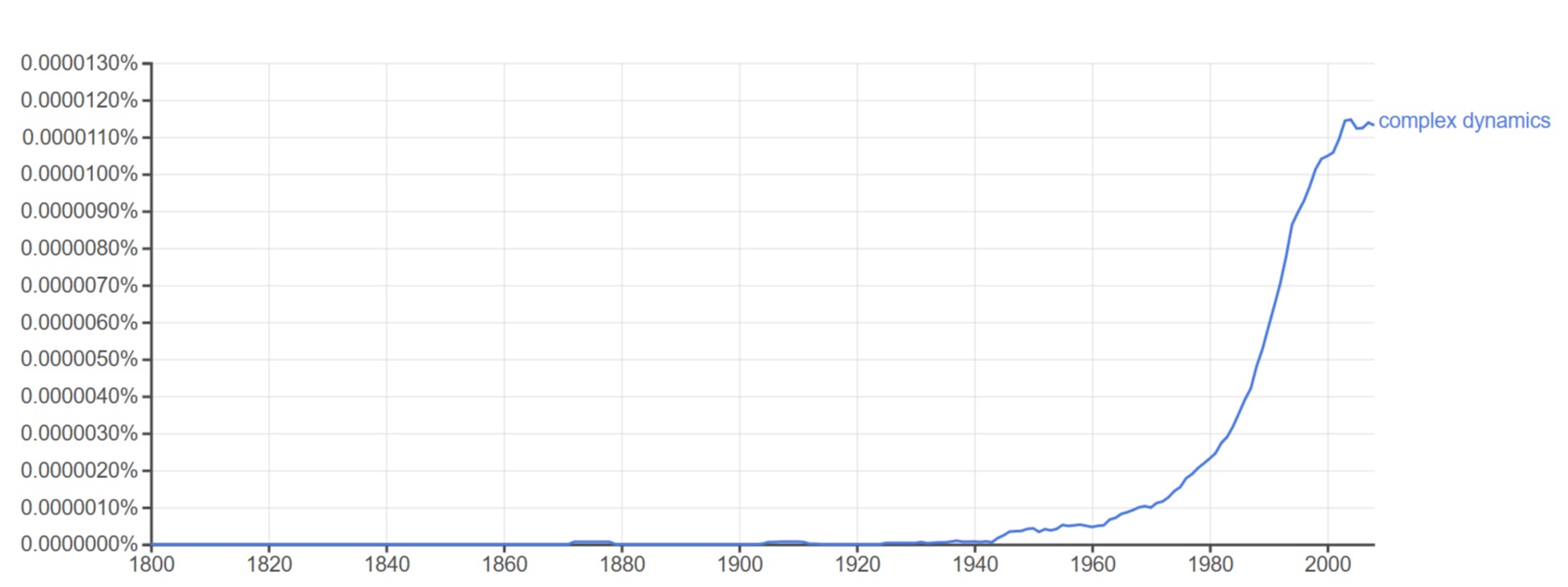
By 1994 complex dynamics, barely in existence for a decade at this point, had become sufficiently established that a history of the subject could be written, Daniel Alexander’s A History of Complex Dynamics. In the current LCC system, a book on the history of complex analysis would be classified preferably under QA331, which includes historical works, or it might be classified directly under QA331.7, for works on complex analysis itself. Despite its title Alexander's book is a history of part of complex analysis, and it should be classified under QA331 or QA331.7. Instead it was assigned the call number QA845, which places it among books on analytical dynamics in physics. This classification was a mistake. Complex dynamics involves iteration of polynomials, whereas analytical dynamics examines the motion of a system of bodies acted upon by forces. The title itself may in fact have been an ahistorical afterthought, since the term complex dynamics appears nowhere in the eight chapters of Alexander’s monograph, which consists of a conventional survey of complex iteration from the 1870s to the 1920s. (Except for its title the book makes little reference to the recent subject, although the latter is clearly the raison d'être for its creation.)
Traditionally researchers in the part of complex analysis that would later be called complex dynamics, among them Paul Montel and Gaston Julia, primarily published articles in journals. Indeed, the abundant journal literature and almost complete absence of books would suggest that the topic of complex iteration lacked any particular identity within the broader domain of complex analysis. Nevertheless, Montel wrote Leçons sur les séries de polynomes à une variable complexe in 1910, a book that was assigned the LCC classification QA332. At the end of the Twentieth century the traditional theory was extended and transformed qualitatively and became a somewhat different subject with the lines of investigations opened up by modern computers. Nevertheless, Carleson and Gamelin’s book of 1993 has the call number QA331.7, the designation for books on complex analysis after 1990, and this was also the number assigned to John Milnor’s Dynamics in One Complex Variable of 2000.
In the current online LC catalogue Alexander’s History of Complex Dynamics is given the call number QA297.8, in the subject area of iteration, and this call number is also assigned to the author’s later book, written with Felice Iaverno and Alessandr Rosa, titled Early Days in Complex Dynamics (2011). These assignments, while an improvement on QA845, might still be questioned, because other books with this call number deal in various ways with iteration but not with complex iteration. Robert L. Devaney and Linda Keen’s collection, Complex Dynamics: Twenty-five Years after the Appearance of the Mandelbrot Set (2006) has the call number QA614.86, a classification that includes books on fractals. The current preferred classification for books on complex dynamics appears to be QA614.8. The subject has migrated from a topic within complex analysis to one of a set of subjects involving dynamical systems, chaos and fractals.
It is worth noting that the term complex dynamics is sometimes applied more generally to the use of complex analysis in the investigation of dynamics as this word is understood by mathematical physicists. For example, Vladamir G. Ivancevic and Tijana T. Ivancevic's Complex Dynamics: Advanced System Dynamics in Complex Variables (2007) includes the iteration of complex polynomials (leading to the Mandelbrot set) but the primary emphasis is on mathematical physics (quantum theory and relativity). This book has the call number QA845, placing it among books on mechanics.
As we move closer to the present the question of the LCC classification of mathematics books becomes moot, since they are increasingly published in electronic form and don’t have a call number. It is also true that older books are being re-released in electronic form, without their LCC call numbers. At least for technical subjects such as mathematics, questions related to library book classification have diminished in importance, and will continue to do so in the future.
6. Mathematical Reviews and the Mathematics Subject Classification Scheme
6.1 Establishment of Mathematical Reviews
Since the Nineteenth century most creative mathematical research has appeared in journals. Classification schemes for this literature are essential to understanding the subject organization of mathematics. Several abstracting and review journals for mathematics were established in the second half of the Nineteenth century covering both journals and books. The most important of these was Jahrbuch über die Fortschritte der Mathematik, discussed by us in Section 4 [17].
Over the years a substantial delay developed between the publication of articles and books and the appearance of their reviews in the Jahrbuch. By the late 1920s this delay had grown to around seven years. In 1931 Göttingen mathematicians Otto Neugebauer and Richard Courant founded the Zentralblatt für Mathematik und ihre Grenzgebiete to achieve a timelier review of the mathematical literature. The first editor of the Zentrablatt was Neugebauer, who retained this position following his refusal in 1934 to sign an oath of loyalty to the government and his subsequent move to Copenhagen. In 1938 Neugebauer resigned as editor of the Zentrablatt and emigrated in the following year to America, where he became a professor at Brown University in Providence, Rhode Island [18].
In 1940 the American periodical Mathematical Reviews (hereafter MR) came into existence. (On the early history of MR see Pitcher 1988.) The establishment of MR was in part a response to problems with Zentralblatt in the late 1930s, including its removal of the Jewish editor Tullio Levi-Civita, the exclusion of Russian and Jewish reviewers and the resignation of several prominent international reviewers. In addition, the rise of the United States as a scientific center, the sheer size of the anglophone mathematics community in the United States and the British Commonwealth, made the creation of MR a natural step. Neugebauer and the Russian-American analyst Jacob Tamarkin became the first editors of MR, which was headquartered in Providence. MR was supported by the Rockefeller Foundation, the Carnegie Corporation, the American Philosophical Society and received subventions from both the AMS and the MAA. These benefactors allowed for subsidized subscriptions to the journal and supported a microfilm service offered to subscribers. It was asserted that the latter “should be of greatest value to mathematicians located in the smaller universities and colleges and should be a factor in encouraging young men to continue with their investigations” (MAA 1939). In 1965 MR moved to Ann Arbor, Michigan adjacent to the University of Michigan where it remains to this day.
From the beginning Mathematical Reviews has solicited reviews from professionals in the field, a group that has grown in size up to the present. (The present writer, although not a major contributor, has published some sixty reviews in MR over the years.) Both periodicals and books are covered, although reviews for the former are much larger in number. MR’s policy is to have reviews by third-party authorities rather than author-abstracts, so the reviews are both informative and evaluative. The reviews vary in length and style and are edited by the staff at MR.
The selection of subject areas and their ordering in MR followed Zentrablatt closely, and the latter in turn followed the Jahrbuch. Table 1 gives the table of contents for the Jahrbuch (1871), Zentralblatt (1939) and MR (1940). The hierarchical conception of mathematics adopted by the reviewing agencies was also at the basis of the subject organization in the QA section of the Library of Congress. This subject selection and ordering forms the basis for the Mathematics Subject Classification (examined below, Section 6.2). Since the latter has become canonical and appears certainly to be the basis of all future classification of mathematical knowledge, the Jahrbuch was evidently a seminal journal for the history of mathematical subject classification. Concerning it, Göbel (2008, 10) observes: "The chapter classification was changed and deepened over the years in order to keep pace with current developments in the various fields of mathematics. Later, these sections formed the basis for the construction of a mathematics classification” [19]. On the subject organization of the Jahrbuch, Bartle (1998, 213) writes, “One might be struck by the overall similarity with the present-day classification system used by Mathematical Reviews”. Also notable in all three journals was the attention paid to the history of mathematics, and it was no coincidence that the founding editor of both Zentrablatt and MR, Otto Neugebauer, was a renowned historian of mathematics.
Table 1: Table of contents for Jahrbuch (1871), Zentralblatt (1939), Mathematical Reviews (1940)

MR’s mission statement from 1940 asserts that “MATHEMATICAL REVIEWS will cover not only pure mathematics, but also papers in the borderline fields of applied mathematics”. Applied fields included mechanics, statistics and probability, and some topics in mathematical physics. Nevertheless, the contents of MR in the early years were weighted towards pure mathematics, perhaps more so than was the case for Zentralblatt. The conception of mathematics that was predominate at the middle of the Twentieth century is sometimes characterized as "modern", a term that denotes an emphasis on axiomatic development, a focus on the concept of structure, and a belief in set theory as the appropriate language for expressing mathematics. (For accounts of mathematical modernism see Corry (2003) and Gray (2008).) The modern perspective accentuates the abstract character of mathematics and tends to downplay applications [20]. The viewpoint of modern mathematics is often associated with the French group Bourbaki, but was prevalent among advanced researchers throughout Europe, North America and Asia into the 1960s [21]. Although there was some degree of interest in applications in the 1940 MR, its contents bore the clear imprint of contemporary modernist notions of mathematics.
6.2 The Mathematics Subject Classification (MSC)
6.2.1 Origins of the MSC
The subject classification organization employed by MR in 1940 was somewhat more detailed than the schematic overview presented in Table 1. The full table of the contents for the first volume in 1940 of MR is given in Figure 3.

The 1940 table of contents provided the rough template for all classification schemes at MR up to the present. By the late 1950s modifications were made to some of the subject headings. For example, differential equations were split into two separate headings, ordinary differential equations and partial differential equations. Algebraic geometry, which until 1959 was grouped with geometry, was moved to an earlier position in the classification under algebra. Although there were a few other minor adjustments, most of the subject headings were retained.
The two-digit subject codes which later became standard first appeared in early 1960 in the index to volume 20 (1959) of MR. Numbers selected from the range 02 to 98 were attached to the 59 subject headings that had been used in the monthly issues and that had appeared in the table of contents at the beginning of the volume. Up until 1959 the annual alphabetic subject indexes had provided a more detailed subject breakdown than the one given by the subject headings. This more fine-grained classification was built into the 1959 coding, with each subject divided into classes, and each class being indicated by a two-digit decimal number. For example, in the period 1940-58 the category of semigroups was listed under groups in the annual subject indexes. In the 1959 coding, semigroups had the designation 20.80. Here 20 was the subject number for groups and generalizations, while 80 was for semi-groups. The code for ordinary differential equations in Banach spaces was 34.95. Here 34 was the number for ordinary differential equations, and 95 was for equations in Banach spaces.
The passage from the annual subject index in 1958 to the one in 1959 was not simply a matter of introducing codes. The shift represented the crossing of a divide. Before 1959 all subjects in the index were listed alphabetically, and classes under these subjects were also listed alphabetically. The 1959 index listed subjects by their place in the table of contents, and the classes under each subject were ordered according to some conception of the natural relationships that existed among them.
The final issue of MR for each year from 1960 until the end of the decade consisted of an index that included a table of subject headings with codes, following the template established in volume 20. Although there was a fair degree of stability in the set of the subject headings and the corresponding two-digit codes, the classes assigned under each code were very much in flux. In some cases, codes contained a three-digit decimal suffix, an indication of how detailed the classification scheme was becoming. A certain level of stability was reached by 1968, two years prior to the emergence of MSC1970.
It should be noted that until the late 1970s subject codes did not appear in regular issues of MR and were not a prominent feature of the journal. They arose as a point of interest only in the index volumes at the end of each year and were likely little noticed by an average user of the journal. It is possible that their primary purpose during this period and even later concerned the role they played within the internal operations of MR in classifying the large volumes of literature coming to it for classification.
6.2.2 Mathematics Subject Classification
The 1968 classification system provided the basis for the Mathematics Subject Classification scheme of 1970. MSC1970 was not motivated by any particular interest in classifying the contents of MR. Its origins were more mundane. A reader of an issue of MR could simply consult the table of contents and go to the subject section corresponding to his or her area of mathematical interest. By contrast, in order to efficiently process requests for offprints or titles it was useful to have a formal system of classificatory codes. Hence the motivation to develop the MSC came in the late 1960s from the AMS's Mathematical Offprint Service (MOS) and its successor the Mathematical Title Service (MTS). The AMS stated that the MTS was “a discipline-wide system for selective dissemination of the titles of papers […] The essential factor in the successful operation of MTS is precise and complete classification. To facilitate such classification, the AMS (MOS) Subject Classification Scheme (1970) was developed” (AMS 1972, 73). It was under the auspices of the MOS and MTS that the MSC was created and maintained during its early years. The codes did not accompany the reviews that appeared in the regular issues of MR, but were published by the MTS in the Index of Mathematical Papers published twice annually. According to Pitcher (1988, 145), at some point the functions of the MTS were taken over by MR and the MSC was administered by the editorial staff of MR [22]. The MTS itself was discontinued.

Figure 4 is the table of contents for both the 1968 and 1970 volumes of MR. In the 1968 classification scheme there were 57 subject areas and 900 classes placed under these headings, which evidently required some substantial deliberation about class definition and identity. (For the detailed 1968 Subject Classification see AMS (1968).)
In the 1970 MSC scheme the number of classes and subclasses increased from 900 to 1900, an expansion that must have involved much further classificatory labor. The 1970 scheme maintained the subject whole numbers, but added a letter of the alphabet to indicate a class. Further topic divisions within this class were indicated by a two-digit number [23]. For example, representation theory of symmetric groups now received the code 20C30. Here 20 as before was the subject area of group theory, C indicated representation theory of finite groups, and 30 was for representation of symmetric groups. Boundary value problems in nonlinear ordinary differential equations was now designated 34B15, with 34 for ordinary differential equations, B for boundary value problems and 15 for non-linear equations. (The full MSC1970 is given in AMS (1972, 73-199) and Fang (1972, 34-57).)
A publication under review would have a primary classification code, and possibly also a secondary classification code, and even additional codes if that was appropriate. The contents of each issue of MR were organized under the subject headings in Figure 4. The subject contents were not further divided by classes. Rather the full MSC codes for reviewed publications were bibliographical constructions that were used in the early years by the MTS to connect the research interests of subscribers to the contents of MR.
Two-digit MSC codes appeared in 1977 for the first time in the table of contents of the first volume of MR for that year. They also appeared beside each subject heading and at the top of every page. During this period three-digit codes (two-digit subject number and class letter) were employed in the AMS’s periodical Current Mathematical Publications. In 1980 two-digit subject codes were provided for each review in regular issues of MR and became a more integral part of the journal. By the 1990s every review in an issue of MR was accompanied by its full 5-symbol MSC code, according to the latest version of the MSC at the time of publication.
In the first half of the 1980s MR published a series of subject index volumes covering its first 40 years: in 1981, for the period 1973-1979; in 1983, for 1940-1959; and in 1985, for 1959-1972. The organizational principle adopted in these indexes for each period reflected the original subject organization used at the time of publication. The subject index for 1973-1979 used MSC1970 as the basis for classification and categorized reviews according to their five-symbol subject-class-subclass designation. The index for 1940-1958 employed a very detailed breakdown on an alphabetical basis, presenting the subjects alphabetically with classes under these subjects also listed alphabetically. Presumably this approach was adopted because no system involving subject coding existed between 1940 and 1958. Nevertheless, the classification was remarkably detailed, much more so than the actual subject-heading organization of the original volumes. Finally, for the period 1959-1972 the 1968 classification was adopted as the standard, apparently because 1968 represented the final product of the evolving annual schemes used from 1959 until then. It should be noted that although the MSC1970 was already in place for the three years 1970-1972 it was not used as the classification standard in the 1985 index volume for 1959-1972.
In the 1970s, Zentrablatt also adopted the MSC and the two reviewing agencies have worked together in revising the classification system. Major revisions occurred in 1980, 1991, 2000, 2010 and the latest revision will appear in 2020. The process of revision is a joint project of the editorial staffs of Mathematical Reviews and Zentralblatt in consultation with the mathematical community. The MSC has moved far beyond its initial involvement in title-retrieval to become the dominant system today for classifying mathematics. In contrast to library classification systems, it has no competitors. As more of the book literature appears in electronic form without call numbers, MSC will be the default classifier, and its dominance will continue to grow. Traditional library systems such as LCC and Dewey will increasingly fall by the wayside.
The number of subject headings appearing in MR increased from 37 in 1940 to 60 in 1970, the latter including several subjects that did not exist or were present only in a nascent form in 1940, among them category theory, optimal control, computing machines, operations research and game theory. While the number of subject headings has not increased dramatically in the different revisions of the MSC that have taken place since 1970, there have been large increases in subject classes and divisions within these classes.
A trend that was evident in 1970 and has intensified up to the present is the very wide view taken of the scope of mathematics, far exceeding the range assumed for mathematics by Library of Congress or by what is covered in a university department of mathematics. In addition to the traditional core areas (foundations, algebra and number theory, analysis, and geometry) a considerable part of physics and astronomy is within MR’s domain, and there are also present subjects in chemistry, biology, engineering, medicine, economics and sociology. The science categories in Library of Congress are QA (mathematics including mechanics), QB (astronomy), QC (physics), QD (chemistry), QE (geology), QH (natural history), QK (botany), QL (zoology), QM (human anatomy), QP (physiology), and QR (microbiology). Engineering subjects in LCC are classified under T, medicine is under R, psychology is under B, and social sciences (including economics) are under H. MR reviews publications from all of these subjects, if the work in question makes substantial use of mathematics. The situation has changed from the early days of MR, when virtually all book literature reviewed was in the QA subject category.
By the mid-1960s MR was republishing reviews from journals in ancillary fields, including Applied Mechanics Reviews, Computing Reviews, Electrical and Electronics Abstracts, Physics Abstracts and the Soviet abstracting journal Referativnyi Žurnal Matematika (Mechanika, etc.). In subsequent years Statistical Theory and Method Abstracts was added to this list. Although these reprints were only a very small percentage of the reviews published in MR, they indicated some degree of interaction with sciences allied with mathematics.
6.2.3 The arrival of MathSciNet
The online version of MR, MathSciNet, was established in 1996, and has replaced the printed edition, which was discontinued in 2012 [24]. Similarly, Zentralblatt has been replaced by the electronic reviewing service zbMath. Both MathSciNet and zbMath use the MSC. Entering either the title or author of a publication in MathSciNet, one is taken directly to the review, which also includes the MSC primary and secondary codes for the publication under review. Entering an MSC classification code leads to all reviews for publications with this classification. One can search according to year and publication type, under book, journal, and proceedings, or all three.
The main document on the AMS website giving information concerning the MSC classification system contains statements about literature predating 1968 that must be read carefully [25]. The assertion “The MSC classification has been revised a number of times since 1940” is incorrect because the MSC did not exist until 1970. The classification scheme from 1940 to 1958 represented by subject headings took place without any codes and remained stable during these years. In MR volumes of the mid 1960s individual reviews were not assigned codes, although in the subject classification for the years 1959-1972 published in 1985 they were retroactively given codes according to the 1968 system. MathSciNet has adopted the 1985 convention in assigning codes for the period 1959-1972.
The assignment of codes to reviews from 1940 to 1958 apparently posed a challenge for MathSciNet. Here are how subject codes were applied to literature appearing in the first volume in 1940 of MR. If a given subject heading in 1940 was also a subject heading in 1970 then it was assigned the same code as the one in MSC1970. For the majority of subject headings this was true and thus many of the codes are the same as the ones in 1970. In cases where some revision to the subject headings occurred, it was necessary to improvise. As we noted above, until 1955 articles on ordinary differential equations and partial differential equations were grouped under the subject heading “Differential equations”. In 1956 this heading was replaced by the two headings, “Ordinary differential equations” and “Partial differential equations, and in 1959 these two subjects were assigned the codes 34 and 35 respectively. It was apparently not viable to go back to every article pre-1956 under the heading “Differential equations” and determine if it was part of ordinary or partial differential equations. The solution was to introduce a new classification number, and thus the 1940 subject heading “Differential equations” was assigned the number 36, which was not used in MSC1970 and therefore was available.
In most cases differences in the codes assigned to the literature from 1940 to 1958 and MSC1970 are relatively minor, but there are some significant anomalies. For example, algebraic geometry was a subject heading in 1940 and was also one in 1970. The MSC1970 code for algebraic geometry was 14 and so this was the code assigned to this subject in the 1940 volume. However, in 1940 algebraic geometry was placed in geometry, while from 1959 on it was placed in algebra. As one moves through the 1940 table of contents one reaches geometry with numbers 48 and higher, except for the anomalous appearance of algebraic geometry, with the much lower number of 14. The policy used in assigning codes to pre-1959 subjects was not to give a characterization of the older classification on its own terms, but to have codes suitable for retrieving information about this literature in line with the post-1970 MSC world of classification.
There are also some curious aspects concerning the coding of older literature. If one enters “09” into the MathSciNet search engine there results almost 4000 reviews from 1940 to 1961 dealing with aspects of algebra, mainly rings and fields. Nevertheless, the code 09 only appeared in the subject index for 1960 and 1961, under the heading universal algebra, and only 10 reviews were ever published with this code. The user today has no way of knowing that 09 exists as a code, much less that it covers literature dealing with algebra. This is also true for the code 36 assigned to differential equations [26]. It seems that there is no information in MathSciNet or MR is about the codes assigned to pre-1959 literature. The only way to identify these codes is to take an original review and match the subject heading under which it appeared to the corresponding two-digit code assigned to it by MathSciNet when one performs an author or title search for the review.
MathSciNet also indexes a substantial amount of pre-1940 literature, going back to the 1870s. In many cases no classification codes are given, but there is still a fair amount of literature for which they are assigned. Since MR did not exist before 1940 there was no classification scheme to attend to, and so one was free to assign codes at will. MathSciNet took full advantage of this situation. The pre-1940 literature is given complete five-symbol MSC1970 classification codes. For the two-digit part of the code for ordinary differential equations, an article from 1906 is assigned the code 34, from 1940-1955 the code 36 and from 1956 on the code 34 [27].
Some further examples from MathSciNet illustrate the shifts in classification that have occurred over the years. We consider the subjects of set theory and celestial mechanics. Set theory went from foundations between 1940 and 1958; then to set theory alone (04) between 1959 and 1999 [28]. In MSC2000, mathematical logic and foundations were given the code 03; 02 and 04 were abolished; and set theory was returned to logic and foundations, and given the code 03E. In MathSciNet, Abraham A. Fraenkel and Yehoshua Bar-Hillel's Foundations of Set Theory (1958) has the code 02, because it was included under the subject heading of foundations in the issue of MR in which it appeared in 1958 and 02 is the code for foundations in MSC1970. Nicolas Bourbaki's Elements of Mathematics Theory of Sets (1968) has the code 04 because it was included under the subject heading set theory in MR in 1968 and 04 was the code for set theory in 1968.
Celestial mechanics, including mathematical work on the three-body problem, was placed at the founding of MR within astronomy, where it remained until 1970. In that year it was put under dynamics of a system of particles and given the designation 70F15. Astronomy in MSC1970 has the code 85. This number is also given to all reviews in MR before 1970 that were included under the subject heading of astronomy at the time of their publication, including celestial mechanics. Theodore E. Sterne's An Introduction to Celestial Mechanics (1960) has the MSC code 85. The link to 85 in MathSciNet states that this code is for astronomy and astrophysics since 1940; also noted is the fact that the code for celestial mechanics since 1970 is 70F15.
The call number of a book identifies the part of mathematical knowledge to which the subject of the book belongs. The call number system — whether it be LCC, Dewey, or anything else — provides a representation of the division of mathematical knowledge into subjects. The call number is also an identifier that allows one to retrieve the book from the library's collection. A system of library classification has the dual function of book retrieval and intellectual subject organization. By contrast, the MSC is a bibliographic classification system. The MSC subject classification code is used to assist the reader in identifying the literature corresponding to a given code. It is not the unique identifier of any particular publication. (Of course, each review has an identification code (currently of the form MRxxxxxx), but this code has no inherent classificatory meaning or relation to the item under review.) Instead one uses the author or title and then is led by a search to its review. The MSC classification code is not required to do this. One can be a consistent user of MathSciNet without knowing specific MSC codes, an obvious difference from a library, where call numbers are necessary to find the books.
Beginning in the 1980s and 1990s mathematics books have generally included the MSC codes with the publishing data presented at the beginning of the book. Since the 1950s this data had traditionally included the LC call number and sometimes also the Dewey classification. As we move closer to the present one finds more and more only the MSC codes given. For books that are only available electronically and where there are no library call numbers, the MSC codes are all there is, in terms of situating the book within the framework of mathematical knowledge. In a world in which books and journals are released electronically a traditional library call number is unnecessary, but a classification code remains valuable, even more so given the pace of subject growth and its continual fragmentation into specialties. A system of classification is evidently also required in order for search engines to work effectively. MSC codes have become ubiquitous: they are required on papers submitted for publication, they must be included for a paper presented at a conference, and they are given at the beginning of books. MSC2010 has 63 subject headings and around 2700 subclasses, and that number will likely increase in 2020. While the MSC may have become a ramified system of some complexity, it fulfills a range of functions and will surely loom large in the future.
6.2.4 Final reflections on MSC
A key event in the history of the MSC was the transition in 1959 from the traditional subject index that was ordered alphabetically to one that was based on the place of the subject in the organizational framework provided by the table of contents and the associated coding of subjects and classes. There was a shift in emphasis from retrieving knowledge to organizing knowledge, a tendency that has grown more pronounced in the subsequent history of the MSC up to the present.
The prominence of the MSC scheme today is noteworthy in light of the variable role it plays in practice in retrieving literature on any particular subject or by any particular author. On the website announcing the project to revise MSC210 there is the following admission (AMS 2018): "In the decade since the last revision, keyword searching has become increasingly prevalent, with remarkable improvements in searchable databases". The author of the document nonetheless emphasizes the valuable functions that MSC performs. Codes are used by publishers in several different ways, help arXiv in classifying submissions, and are an aid in organizing paper sessions at conferences.
Current interest in the MSC goes beyond its use in information retrieval and is indicative of a deeper disciplinary interest in the question of the classification of mathematical knowledge. Since the broad classificatory framework at the two-digit subject level is fairly established, attention is channeled to the classes under each subject and the further divisions and orderings within these classes. A fine-grained sense of the vast field that is present-day mathematics is provided by the landscape of the MSC and the periodic revisions that it undergoes.
Daniel Parrochia (2018, 281-282), in a larger study of the place of philosophy in modern mathematics, criticizes the MSC2010 on the ground that is does not reflect underlying connections that exist between different parts of mathematics. Combinatorics has its own subject designation, but combinatorics arises in other subjects, including number theory and theory of Lie groups. Both set theory and category theory are comprehensive theories and for this reason are allied philosophically. Nevertheless, the two theories have separate subject designations, 03 for set theory and 18 for category theory. The Langlands program connects number theory and analysis but this linkage is not apparent in the subject categories of the MSC. Modern thinkers from David Hilbert to Bourbaki have admired the organic unity of mathematics, a unity that is not (in Parrochia’s view) apparent in the MSC.
The MSC was of course not created ex nihilo as an abstract scheme to classify mathematics. Rather it evolved historically and has been modified regularly throughout its history since 1959. Some of the revisions have been substantial, but the core structure of the classification has remained intact. The system of primary, secondary and tertiary classification codes as well as the systematic use of cross-referencing serve to make connections between topics that lie on different subject branches.
Consider the example of set theory and category theory. Subject 18 began as homological algebra in 1959 (homological algebra was not a subject heading until the year before). In 1968, 18 became category theory and homological algebra, where it has remained until today. In MSC2010 there are seven classes in 18 (18A-18G), six of which concern categories and one that concerns homological algebra. Meanwhile, as we saw above, set theory began in foundations in 1940 and migrated to its own subject 04 from 1959-1999, only to return to foundations as a class within 03 in MSC2000. It would be necessary to restructure the classification fairly radically in order to join a subject affiliated historically and substantively with homological algebra to one whose primary origins and character lie in measure theory and foundations.
It is possible that a reorientation of the nature of mathematics could be achieved along the lines suggested by Parrochia (2018, 282-303), making fundamental the theory of categories and sheaves and Alexander Grothendieck’s program. Such a program would be of interest from a foundational and mathematical viewpoint, and is worth pursuing at least on a theoretical level. It might better reflect the organic unity of mathematics but it is not clear that it would provide a basis for the organization of all of mathematical knowledge on the scale of the MSC. As a matter of practical reality, the MSC is so established, extensive and widely used that its central place in the classification of mathematical knowledge is unlikely to be seriously challenged anytime soon.
Acknowledgement
I am grateful to two referees for their detailed comments on a first draft of the expanded paper.
Endnotes
1. LaMontagne (1952, 208) observes that Charles Cutter “foresaw the continuing growth of the library and knew that each change in the shelving of books entailed the changing of "shelf marks" — a long and expensive process. Cutter therefore decided to abandon fixed location “and to adopt a method which would allow books to be moved without changing the marks on the catalogues”. The part in quotation marks is from (Cutter 1882, 6). Cutter’s “bench marks” are what we refer to today as call numbers.
2. The University System of Georgia (2019) asserts: "Libraries in the United States generally use either the Library of Congress Classification System (LC) or the Dewey Decimal Classification System to organize their books. Most academic libraries use LC, and most public libraries and K-12 school libraries use Dewey". This is also true for Canada and some other parts of the British Commonwealth.
3. https://www.loc.gov/aba/dewey/about.html and https://www.loc.gov/aba/dewey/index.html.
4. See endnote 14 below.
5. Flint (1904, 222-223 and 308-312) gives accounts of the classifications of Renouvier and Goblot.
6. English translation is by Thomas J. McCormack from the 1893 English edition of Mach's book, The Science of Mechanics: A Critical and Historical Account of Its Development (Open Court, Chicago).
7. Flint (1904, 277) mistakenly gives the date of publication of Masaryk’s book as 1866. Masaryk was born in 1850 and entered the University of Vienna in 1872.
8. An exception to the prevailing consensus was Karl Pearson, who in his Grammar of Science (1892) put theory of functions and calculus together with arithmetic and algebra, these subjects dealing with quantity, while geometry was classified as a distinct subject area dealing with space (Flint 1904, 296). Earlier the Paris book seller Jacques-Charles Brunet (1814) in his pioneering classification scheme placed mathematical subjects in the order arithmetic, algebra, calculus, and geometry. Brunet was presumably influenced by Comte and Ampère. Brunet's catalogue was exceptional among all classification schemes in placing mathematics at the end of the sciences, following philosophy, physics, chemistry, geology, biology, and medicine.
9. The Universal Decimal Classification (UDC) is a bibliographical and library classification system that was influenced in its origins by Dewey but developed into an important international service of its own that is widely used today. McIlwaine (1997) provides an historical study of the UDC. Its ordering of mathematical subjects follows older Dewey: foundations, number theory, algebra, geometry, analysis. It is also of interest to consider the subject ordering adopted by encyclopedias of mathematics. The influential Japanese Iwanami Sugaku Ziten (Encyclopedic Dictionary of Mathematics) (Japanese Mathematical Society 1954) posits the order arithmetic, algebra, geometry, analysis. Subsequent editions appeared in 1960 and 1968. Fang (1972) devotes chapter 4 of his book to the Iwanami. Fang regards it as a work of “obvious greatness” (17). An English translation was published by MIT Press in 1977.
10. On the formative place of the Jahrbuch in the modern classification of mathematics see Section 6.
11. An interesting graphical illustration of this change in usage is provided by the Google Ngram (Michell et al. 2011) for the terms “theory of functions” and “complex analysis” for the period from 1880 to 2008. See Figure 1.
12. While there is certainly a general conservatism among librarians with respect to classification, in the case of the Dewey there have been revisions of the classification that have been retroactively applied by some libraries to books in their collections. See the discussion below of the University of Illinois at Urbana-Champaign.
13. At least in some quarters today there is still a preference for placing geometry before analysis, in accordance with traditional nineteenth–century notions of mathematical classification. The American Mathematical Society in tracking new PhDs uses the subject order: foundations, algebra/number theory, geometry/topology, analysis. The National Science Foundation in the United States organizes its science programs in the order: algebra/number theory, topology/foundations, geometrical analysis, analysis. The International Mathematics Union divides the lecture sections at its congresses into the categories: foundations, algebra, number theory, algebraic geometry, geometry, topology, Lie theory, analysis. (See Dave Rusin, "The Divisions of Mathematics", http://web.archive.org/web/20150516041021/http://www.math.niu.edu/~rusin/known-math/index/tour_div.html. See also, http://web.archive.org/web/20150424115620/http://www. mathunion.org/activities/icm/icm-2010-program-structure/.)
14. I am grateful to Michael Norman, Head of Content Access Information at the UICC, and Tim Cole, Head of the Mathematics Library at UICC, for information about their collection (emails, November 27 and 28, 2016). Tim Cole reports that there were further revisions of the Dewey system with Dewey 22 (2003), but that these revisions were more minor than the ones in schedule 18. The Mathematics Library has not updated books before 2003 to the specifications of schedule 22. There have been further minor revisions to mathematics classification since 2003. Today the UICC relies mainly on the Dewey call numbers for new books provided by the Decimal Classification Division of the Library of Congress. The UICC is also moving in the direction of classifying new books using the LC classification system itself.
15. There was not complete consistency in cataloguing during the transition years between about 1968 and 1972. It should also be noted that books on real analysis were sometimes assigned 517 rather than 517.5 (before 1971) and 515 rather than 515.8 (after 1971).
16. Although there was a great deal of research on dynamical systems at the end of the twentieth century, it did not receive its own two-digit subject heading in AMS’s Mathematics Subject Classification (discussed in the next section) until the year 2000. Literature under this subject heading has expanded greatly since then.
17. An account of reviewing and bibliographical journals for mathematics during this period is given by Pemberton (1969, 55-60).
18. The history of the Jahrbuch and Zentrablatt in the 1930s and 1940s is documented by Siegmund-Schultze (1993), although the subject of classification is not raised. A short account of Zentralblatt in the first two decades of its existence is given by Ett and Welt (1998).
19. "Die Kapiteleinteilung wurde im Laufe der Jahre geändert und vertieft, um mit aktuellen Entwicklungen auf den verschiedenen Gebieten der Mathematik Schritt zu halten. Später bildeten diese Abschnitte die Grundlage für den Aufbau einer Mathematik-Klassifikation."
20. Siegmund-Schulze (1993, 133-136) observes that in the 1930s a more structural approach to mathematics was evident in abstract algebra and functional analysis, a trend that intensified despite the influence of such German mathematicians as Ludwig Bieberbach, who favored a more intuitive and down-to-earth "Aryan" approach to mathematics.
21. The American movement in the 1950s and 1960s to overhaul primary and secondary school mathematics education — the so-called new mathematics — was deeply influenced by contemporary modern mathematical perspectives. See Hayden (1981) for a history of the new math movement.
22. Writing apparently on behalf of the AMS, Pitcher (1988, 145) states, "Repeated offers to assist with a revision of the Dewey Decimal Classification of mathematics, universally recognized as ineffective and outdated for research mathematics, have been refused”. At the time the MSC scheme was being developed, Dewey classifiers were already working on schedule 18 which included a reclassification of mathematics books. It is possible that this was the reason the Dewey people were not receptive to the AMS offers. See endnote 10 above.
23. In principle, the 1968 classification allowed for 100x100=10,000 subclasses. By contrast, this number for MSC1970 was 100x26x100=260,000. MCS1970 also had other classificatory advantages connected to the use of letters to designate broad topic categories.
24. We do not in this article consider technical matters related to the creation of MathSciNet or the platform for its application. On this subject, see Gala et al. (2019).
25. This document is at https://mathscinet.ams.org/mathscinet/help/field_help.html#mscp.
26. The user who enters 34 for ordinary differential equations into MathSciNet and discovers the absence of any returns for the fifteen-year period from 1940 to 1955 will view this as a mystery, and will have no way of knowing that entering 36 would produce the missing reviews.
27. There is some literature on ordinary differential equations from the period 1949-1955 that is given the classification 34 in MathSciNet but the reviews in question appear in volumes of MR for 1956 and 1957. The subject heading "ordinary differential equations" appeared for the first time in volume 17 in 1956. (The MathSciNet search by year goes by the year of publication of the article rather than the year of publication of the review.)
28. In the 1940s MR there is the subject heading “Theory of sets, theory of functions of real variables”. It is a matter here of the use of sets in real analysis and measure theory. Set theory as we understand it appears under the subject heading.
29. The following volumes of MR were consulted for this article: 1, 6, 11, 16(1), 18(2), 19(1), 19(2), 20(1), 20(2), 22(1), 22(2), 28(2), 29(1), 33(1), 34(2), 36(1), 36(2), 37(2), 38(1), 44(1), 45(1), 46(1), 49(1), 50(1), 51(1), 53(1), 80a-c, 94k-m, Index of Math. Papers (1970), Index of Math. Papers (1971), Subject Index 1973-79 (V. 1-5), Subject Index 1940-1958, Subject Index 1959-1972 (V. 1-4), Subject Index 1980-84 (V. 1), Current Math. Publications (V. 9 and 22).
30. Brunet (1814). In an appendix the translator gives a statistical breakdown of the contents of Brunet’s bookshop, using the total number of bench marks or call numbers each subject receives as a percentage of the total number of bench marks overall. Arts and Sciences constituted 22.7% of the contents of the collection, while the mathematical sciences constituted 15.2% of Arts and Sciences. From this one may deduce that the mathematical sciences represented 3.5% of the overall collection.
References
Alembert, Jean d'. 1743. Traité de Dynamique. Paris: David l'ainé.
Alexander, Daniels S. 1994. A History of Complex Dynamics from Schröder to Fatou and Julia. Braunschweig and Wiesbaden: Friedr. Vieweg & Sohn.
Alexander, Daniels S., Felice Iaverno and Alessandr Rosa. 2011. Early Days in Complex Analysis A History of Complex Dynamics in One Variable During 1906–1942. Providence, Rhode Island: American Mathematical Society, London Mathematical Society.
American Mathematical Society. 2018. “MSC2020 Announcement of the plan to revise the Mathematics Subject Classification”. https://msc2020.org/. (Accessed October 2019)
American Mathematical Society. 1968. “Subject Index”, Mathematical Reviews 36, July 1968-December 1968. Part 2: 1539-46.
American Mathematical Society. 1972. Index of Mathematical Papers. Volume 1 July-December 1970. Providence, Rhode Island.
American Mathematical Society. No date. Guide to the MSC. [29] https://mathscinet.ams.org/mathscinet/help/field_help.html#mscp. (Accessed October 2019)
Ampère, André-Marie. (1834) Essai sur la philosophie des sciences, ou exposition analytique d’une classification naturelle de toutes les connaissances humaines. Tome 1. Paris: Mallet-Bachelier.
Bain, Alexander. 1870. Logic. Part One: Deduction. London: Longmans, Green, Reader and Dyer.
Bartle, Robert G. 1998. “A Brief History of the Mathematical Literature,” in Electronic Databases and Publishing, edited by Albert Henderson. New York: Transaction Publishers.
Bliss, Henry E. 1929. The Organization of Knowledge and the System of the Sciences. New York: Henry Holt and Company.
Bliss, Henry E. 1933. The Organization of Knowledge in Libraries and the Subject-Approach to Books. New York: The H.W. Wilson Company.
Bliss, Henry E. 1935. A System of Bibliographic Classification. New York: The H.W. Wilson Company.
Bourbaki, Nicolas. 1968. Elements of Mathematics Theory of Sets. Paris: Hermann.
Brown, James Duff. 1906. Subject Classification, with Tables, Indexes, etc. for the Sub-division of Subjects. London: Library Supply.
Brunet, Jacques-Charles. 1814, 1860. Manuel du libraire et de l’amateur de livres. Paris: Dido Frères. The first edition of this work was published in 1814. An English translation and introduction by Donald Bruce McKeon of the 1864 edition appeared in 1976 as The classification system of Jacques-Charles Brunet, Baton Rouge: Louisiana State University Graduate School of Library Science (Occasional Papers, No, 1). [30]
Brunet, Jacques-Charles. 1860, 1864. Manuel du libraire de l’amateur de livres. Tome premier. Paris: Librairie de Firmin Didot Frères, fils et Cie. Five more volumes appeared up to 1865.
Comte, Auguste. 1830. Cours de philosophie positive. Tome premier Contenant les préliminaires généraux et la philosophie mathématique. Paris: Rouen Frères.
Corry, Leo. 2004. Modern Algebra and the Rise of Mathematical Structures. Second revised edition. Basel: Birkhäuser.
Cutter, Charles A. 1882. Boston Athenaeum; How to Get Books, With an Explanation of the New Way of Marking Books. Boston, MA: Rockwell Churchill.
Cutter, Charles A. 1891-93. Expansive Classification. Part I: The First Six Classifications. Boston: C. A. Cutter.
Devaney, Robert L. 1987. An Introduction to Chaotic Dynamical Systems. Redwood City, California: Addison Wesley Publishing Company.
Devaney, Robert L. and Linda Keen. 2006. Complex Dynamics: Twenty-five Years after the Appearance of the Mandelbrot Set. Providence, Rhode Island: American Mathematical Society.
Dewey, Melvil. 1876. A Classification and Subject Index for Cataloguing and Arranging the Books and Pamphlets of a Library. Amherst, Mass.: Case, Lockwood & Brainard Company.
Dolby, Robert G. A. 1979. “Classification of the Sciences: The Nineteenth Century Tradition.” In Classifications in their Social Context, edited by Roy F. Ellen and David Reason. New York: Academic Press, 167-93.
Ellen, Roy F. and David Reason. 1979. Classifications in their Social Context. New York: Academic Press.
Erdlund, Paul. 1976. “A Monster and a Miracle: The Cataloging Distribution Service of the Library of Congress, 1901-1976”. The Quarterly Journal of the Library of Congress 33: 383-421.
Ett, Walter and Reiner Welk. 1998. “Zentralblatt für Mathematik und ihre Grenzgebiet”. In Mathematics in Berlin, edited by H.G.W. Begehr et al. Berlin: Birkhäuser Verlag, 189-90.
Fang, Joong. 1972. A Guide to the Literature of Mathematics Today. Hauppauge, N.Y.: Paideia.
Flint, Robert. 1904. Philosophy as Scientia Scientiarum and History of Classifications of the Sciences. Edinburgh and London: William Blackwood and Sons.
Fraenkel, Abraham A. and Yehoshua Bar-Hillel. 1958. Foundations of Set Theory. Studies in Logic and Foundations of Mathematics. Amsterdam: North-Holland.
Fraser, Craig. 2017. “Mathematics in Library Subject Classification Systems”. Research in History and Philosophy of Mathematics Proceedings of the Canadian Society for the History and Philosophy of Mathematics/La Societé Canadienne d’Histoire et de Philosophie des Mathématiques, edited by M. Zack and D. Schlimm. Springer International Publishing Switzerland, 181-97.
Gala, Lauren, Jeffra Diane Bussmann and Anya C. Bartelmann. 2019. “MathSciNet: A Comparative Analysis of American Mathematical Society and EBSCO Platforms”. Journal of Electronic Resources Librarianship 31, no. 1: 1-13.
Gleick, James. 1988. Chaos: Making of a New Science. New York: Viking Books.
Göbel, Silke. 2008. “Die Anfänge des Wissensmanagements in der Mathematik: das „Jahrbuch über die Fortschritte der Mathematik “”. In Mathematik in Blickpunkt, edited by Bernd Wegner. FIZ Karlsruhe, 9-13.
Goblot, Edwin. 1898. Essai sur les classifications des sciences. Paris: Germer Baillière.
Gray, Jeremy. 2008. Plato’s Ghost: The Modernist Transformation of Mathematics. Princeton, NJ.: Princeton University Press.
Hacking, Ian. 2014. Why Is There Philosophy of Mathematics at All? Cambridge, UK: Cambridge University Press.
Hayden, Robert. 1981. A History of the “New Math” Movement in the United States. PhD dissertation, Iowa State University. ProQuest Dissertations and Theses.
Herschel, William. 1802.” Catalogue of 500 New Nebulae, Nebulous Stars, Planetary Nebulae, and Clusters of Stars; With Remarks on the Construction of the Heavens”. Philosophical Transactions of the Royal Society 92: 477-528. Reprinted in The Scientific Papers of Sir William Herschel Volume 2 (1912), 199-237
International Catalogue of Scientific Literature A Mathematics. 1902. London: Royal Society of London.
Ivancevic, Vladamir G. and Tijana T. 2007. Complex Dynamics: Advanced System Dynamics in Complex Variables. Dordrecht, The Netherlands: Springer.
Japanese Mathematical Society. 1954. Iwanami Sugaku Ziten, (eds.) Shōkichi Iyanaga and Yukiyosi Kawada. Augmented edition 1960, second edition 1968. Translated into English under the title Encyclopedic Dictionary of Mathematics (Cambridge, Mass.: MIT Press, 1977). Translation reviewed by Kenneth O. May.
LaMontagne, Leo E. 1961. American Library Classification, with Special Reference to the Library of Congress. Hamden, Conn.: Shoe String Press.
Library of Congress. No date. "The Dewey Program at the Library of Congress". https://www.loc.gov/aba/dewey/index.html. See also https://www.loc.gov/aba/dewey/about.html.
Library of Congress. Library of Congress Classification Class Q Science. 1905. Washington: Government Printing Office.
Mach, Ernst. 1883. Die Mechanik in ihrer Entwickelung historisch-kritisch dargestellt. Leipzig: Brockhaus.
Masaryk, Tomáš. 1887. Versuch einer concreten Logik. Vienna: Verlag von Carl Konegen.
Michel, Jean-Baptiste et al. 2011. "Quantitative Analysis of Culture Using Millions of Digitized Books". Science 331, no. 6014: 176-82. DOI: 10.1126/science.1199644
Mathematical Association of America (MAA). 1939. “Announcement of Mathematical Reviews”. American Mathematical Monthly 46: 614.
McIlwaine, Ia C. 1997. "The Universal Decimal Classification: Some Factors Concerning Its Origins, Development, and Influence". Journal of the American Society for Information Science 48: 331-9.
Meyer, W. F. (Ed.). 1898-1935. Encyklopädie der Mathematische Wissenschaften. 6 volumes. Leipzig: B.G. Teubner Verlag.
Milnor, John. 2000. Dynamics in One Complex Variable. Braunschweig: Vieweg.
Montel. Paul. 1910. Leçons sur les séries de polynomes à une variable complexe. Paris: Gauthier-Villars.
Parrochia, Daniel. 2018. Mathematics and Philosophy. London: ISTE Ltd.
Pemberton, John E. 1969. How to Find Out in Mathematics. Second revised edition. London: Pergamon Press.
Pitcher, Everett. 1988. "Mathematical Reviews". In A History of the Second Fifty Years, American Mathematical Society, 1939-1988. Volume I of American Mathematical Society centennial publications. Providence, RI. Also available online at http://www.ams.org/publications/math-reviews/Pitcher.pdf.
Ranganathan, S.R. 1933. Colon Classification. Madras: Madras Library Association.
Renouvier, Charles. 1859. Essais de critique générale. Paris: A. Colin.
Sayers, W.C. Berwick. 1915-16. Canons of Classification. London: Grafton and Co.
Schaffer, Simon. 1980. "Herschel in Bedlam: Natural History and Stellar Astronomy". The British Journal for the History of Science 13: 211-39.
Siegel, Max Harris. 2016. Book review of Hacking (2014). Why Is There Philosophy of Mathematics at All? Mind 125, no. 497: 252-6.
Siegmund-Schultze, Reinhard. 1993. Mathematische Berichterstattung in Hitlerdeutschland: der Niedergang des "Jahrbuch über die Fortschritte der Mathematik". Göttingen: Vandenhoek & Ruprecht.
Spencer, Herbert. 1864. The Classification of the Sciences. New York: D Appleton and Company.
Sterne, Theodore E. 1960. An Introduction to Celestial Mechanics. New York: Interscience Publishers.
University System of Georgia. Online Library Learning Center. No date. "The Library of Congress Classification System (LC)”. https://www.usg.edu/galileo/skills/unit03/libraries03_04.phtml. (Accessed October 2019)
Whewell, William. 1858. Novum Organon Renovatum: Being the Second Part of the Philosophy of the inductive Sciences. London: J.W. Parker.
Wilson, William D. 1856. Elementary Treatise of Logic. New York: D. Appleton and Company.
Version 1.0, published 2019-10-31, last edited 2019-11-26
Article category: KO in specific domains
The present study is an expanded and revised version of Fraser (2017).
This article (version 1.0) is also published in Knowledge Organization. How to cite it:
Fraser, Craig. 2020. “Mathematics in Library and Review Classification
Systems: An Historical Overview”. Knowledge Organization 47, no. 4: 334-356. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/mathematics
©2019 ISKO. All rights reserved.