I S K O
Encyclopedia of Knowledge Organization
Mathematical theory of classification
by Daniel ParrochiaTable of contents:
1. Introduction
2. A brief history of mathematical classification
3. Examples of classifications and the problem of their formalization
4. Extensional structures: 4.1 From weak to strong structures; 4.2 The lattice of partitions; 4.3 The case of covers
5. Methods for building empirical classifications: 5.1 Distance, metric and ultrametric; 5.2 Algorithms for chains of partitions (5.2.1 Bottom-up methods, 5.2.2 Top-down methods, 5.2.3 Non-hierarchical methods: 5.2.3.1 k-means classifications, 5.2.3.2 Other non hierarchical algorithms); 5.3 Algorithms for covers and weak structures; 5.4 Unsolved problems
6. Intensional methods
7. Classifications and flows of information
8. Towards a general theory of classifications: 8.1 Classifications inside mathematics; 8.2 Searching for an algebra of classifications; 8.3 Some candidates among the algebras; 8.4 A common construction for tree-like classifications and hypercube-like classifications
9. Conclusion: 9.1 The missing theory; 9.2 A philosophical view; 9.3 Final remarks: from continuum to empirical data
References
ColophonAbstract:
One of the main topics of scientific research, classification, is the operation consisting of distributing objects in classes or groups which are, in general, less numerous than them. From Antiquity to Classical Age, it has a long history where philosophers (Aristotle) and natural scientists (Linnaeus) took a great part. But since the 19th century (with the growth of chemistry and library science) and the 20th century (with the arrival of mathematical models and computer science) mathematics (especially theory of orders and theory of graphs or hypergraphs) allows us to compute all the possible partitions, chains of partitions, covers, hypergraphs or systems of classes we can construct on a domain. In spite of these advances, most of classifications are still based on the evaluation of ressemblances between objects that constitute the empirical data. However, all these classifications remain, for technical and epistemological reasons we detail in this article, very unstable ones. We lack a real algebra of classifications, which could explain their properties and the relations existing between them. Though the aim of a general theory of classifications is surely a wishful thought, some recent conjecture gives the hope that the existence of a metaclassification (or classification of all classification schemes) is possible.
1. Introduction
→ Classification is the operation consisting of sharing, distributing or allocating objects in classes or groups which are, in general, less numerous than them. It is also the result of this operation and one of the main topics of scientific research and organization of knowledge (Dahlberg 2014; Hjørland 2017).
Inside science, and especially inside mathematics, what we call a classification supposes the existence of an equivalence relation ℛ defined between the elements of a set E, leading to the quotient set E/ℛ, the set of equivalent classes that can be, afterall, hierarchised. The various elements of the set E are usually compared by the means of some invariant.
For example, partitioning ℕ, the set of natural numbers, into odd and even numbers, supposes you take for invariant their classes modulo 2. Now, if you want to classify the abstract sets in general, then you will have to take for invariant their cardinals. In experimental sciences (physics, chemistry, natural sciences...), there are more complex invariants, such as symmetry groups, discrete groups, and so on.
Invariants are in fact kinds of criteria that allow us to tell whether the objects we compare are similar or not. However, in practical domains, we cannot get always good invariants or indisputable criterias for classifications. Indeed, even in those domains, a simple glance at the problem shows that classification gains by being developed mathematically. Of course we can compare pairs of objects through their attributes, and try to make classifications empirically as, for example, Michel Adanson (1763) did. However, as soon as the number of objects to be classified exceeds a few dozen, processing the operation of classification is very difficult.
Fortunately, since the 1950s, we can use computers. This means that we must previously define the notions of likeness or proximity of two objects, concepts more clearly expressed by a mathematical coefficient of similarity, which is a kind of abstract notion of distance. This latter, in turn, presupposes the notion of metric space. And once we have built sets or classes with some structures defined on them (quasiorder, order, topological space...) in order to make some groupings of the objects, we find ourselves again in pure mathematics. Mathematics are also useful to compare these structures, by the means of powerful tools such as categories and functors. So we get classifications of mathematical structures or, if we make use of logic, especially model theory, classifications of their underlying theories. Finally, we reach foundational problems. Building stable classifications raises a lot of questions that are familiar to a mathematician: the search for invariants, the quest for a metastructure that explains all forms of empirical or formal classifications, finally, the examination of a possible algebra able to reflect the changes of classification schemes and the passage from one classification to another over time. All these facts lead to consider a mathematical theory of classification as a new construction of the continuum (see section 9). However, we must recognize that, currently, there is no single theory of classification.
2. A brief history of mathematical classification
For a long time (say, from Plato and Aristotle to the 17th and 18th centuries), building classifications remained the work of natural scientists (in zoology, botany, etc.) and, as the number of living beings was not so important, did not require any mathematics at all to be performed. However, many problems raised in the taxonomic operations (see Dagognet 1970) and the necessity of a comprehensive theory was already obvious. Indeed, the idea of a general theory of classification, anticipated by Kant's logic (1800) when it describes the possible divisions of attributes, only began to appear in France with Augustin-Pyrame de Candolle (Théorie élémentaire de la Botanique, 1813), who intended to classify the classifications themselves (Drouin 1994, 2001), opposing artificial classifications and natural ones. Then Auguste Comte in his Cours de philosophie positive (1830, lessons 36, 40 and 42) posed a general theory based on the study of symmetries in nature. He was himself influenced by the work of Gaspard Monge in projective geometry (especially his classification of surfaces). However, during a long time, modernity (with an exception for library science in USA, Europe and India) forgot this problem which appeared again only in the 1960s. At this time, the Belgian logician Leo Apostel (1963) and the Polish mathematicians Luszczewska-Romahnowa and Batog (1965a; 1965b) published important papers on the subject. This revival was followed by the new publication of Birkhoff's famous book on lattice theory (1967), which had a certain resonance. In the 1970s, mathematical models of numerical taxonomy (Sokal and Sneath 1973) and hierarchical classifications were developed in the USA and in France with the books of Barbut and Monjardet (1970), Lerman (1970), and Benzécri (1973). All these works assumed of course the big last century advances in mathematical order theory: especially the articles of Birkhoff (1935; 1949), Dubreil and Jacotin (1939), Ore (1942; 1943), Krasner (1944) and Riordan (1958). We must also mention the ancient work of Kurepa (1935) on infinite ramified spaces and the numerous (now >1000) papers of Saharon Shelah on classification theory (see Shelah 1978; 1990) considered as a part of model theory.
3. Examples of classifications and the problem of their formalization
What we have in mind when we speak of classifications in Western countries is often a rigid diagram like those of the classical Age's natural taxonomies, where organisms were grouped together into taxa, these groups being given a taxonomic rank. These diagrams are, in fact, typical examples of hierarchical classifications: see, for instance, the classification of plants based on sexual organs (Linnaeus 1758) (see Fig. 1) or the classification of animals into vertebrates and invertebrates (Lamarck 1801).

In life sciences, this hierarchical model, largely inherited from Linnaeus (kingdom, phylum, class, order, family, genus, species), is always the same. From a mathematical viewpoint, these ordered sequences of divisions are named chains of partitions.
But we encounter also in many domains simple partitions, i.e divisions of a set into nonempty classes, such that the intersection of any two of them is empty and their union is the set itself. Such are the classifications of conics in mathematics (circle, ellips, parabola, hyperbola), or what we can call in other domains cross-partitions, because of the superposition of two or more of them: see, for example, the Mendeleev table of elements in chemistry, formed by a partition of the set of chemical substances into periods of growing weights (lines) and, simultaneously, into chemical affinities (columns). On closer examination, we can see that we may get, indeed, a lot of other forms of classifications: pseudo- or quasi-hierarchies (ordering on intersecting classes), or even simple systems of classes (with no ordering on them). The reason for all this is that we cannot get everywhere strong orders from empirical data and that we must often settle for weaker structures. In some domains, we even fail to get non intersecting classes of the same level. It is the case in social sciences where we sometimes encounter complex realities: these ones are often difficult to put into non overlapping classifications. In particular cases, nonempty intersections between classes of the same level are essential. For example, librarians, in order to optimize information retrieval, usually classify a book in different places, because it is needed, for the reader, to be able to access it by several entries. Formally speaking, it means that one and the same document is located at the intersection of multiple classes. This explains why we must build more complicated schemes than simple partitions or hierarchies. In many situations, fuzzy models (in the sense of Zadeh 1965) extended now to big relational data bases (Meier et al. 2008), or rough sets (in the sense of Pawlak 1982) are necessary, because an object may belong more or less to some class. And a cloudy organization is sometimes better than none. In many domains, as well, partial orders (semilattices or lattices) will be closer to the facts than tree structures (see Fig. 2).
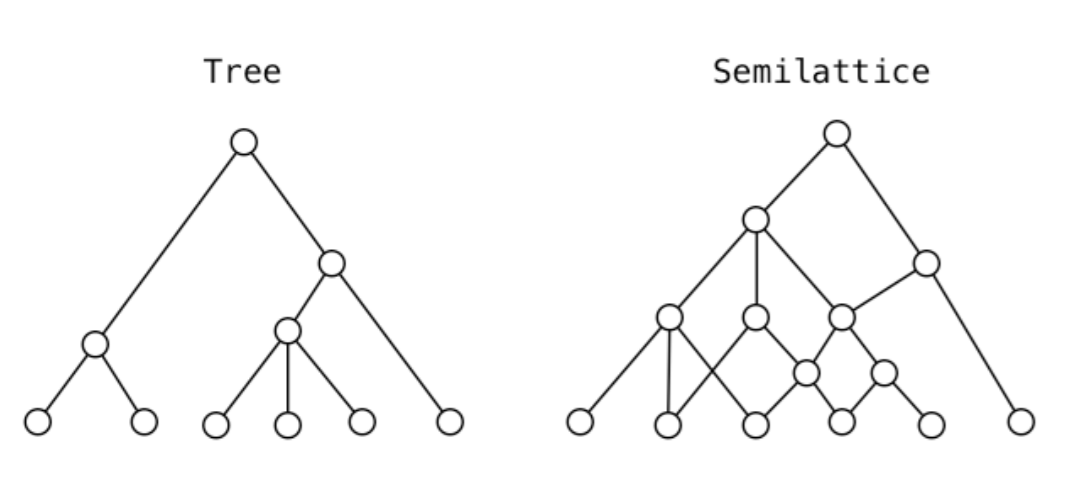
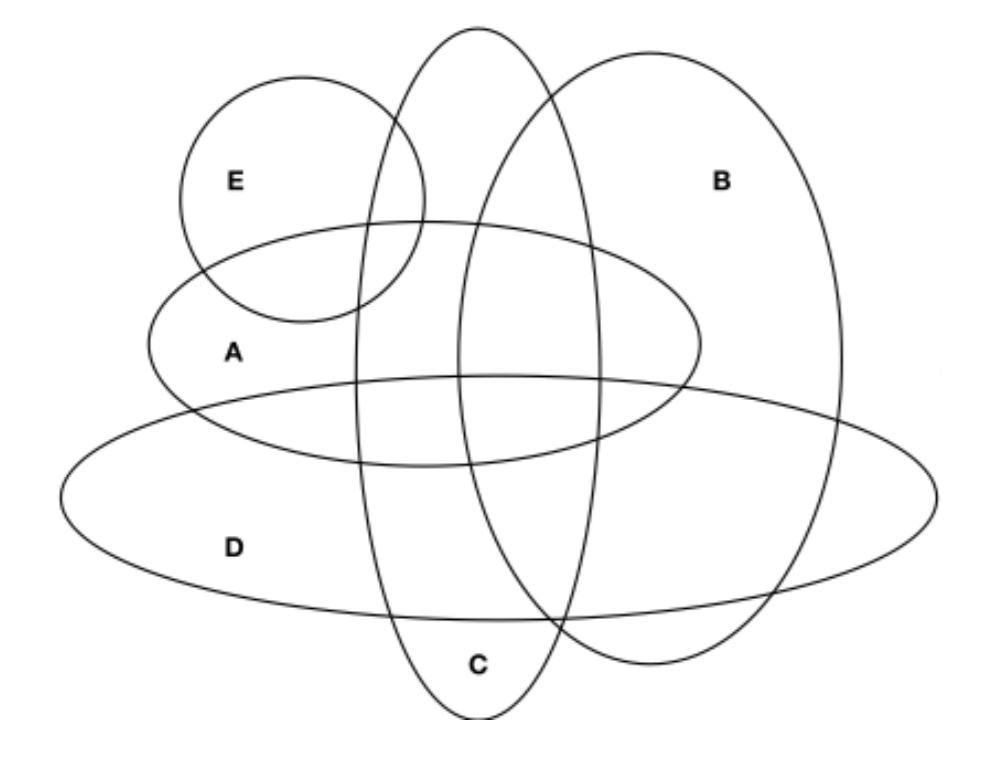
Let us recall here that a (mathematical) tree is a connected graph without any cycle, while a semilattice is just a collection of sets where two overlapping sets belong to the collection, so like the set of elements they have in common. A lattice is just both a upper semilattice and a lower semilattice. These structures are very widespread in social sciences or even urbanism (see Alexander 1965). Let us give another example. Look at what the South-american writer J. L. Borges (see Borges 2001) call the Chinese classification, which classifies the animals of the world into the following classes: A those that belong to the Emperor; B embalmed ones; C those that are trained; D suckling pigs; E mermaids... etc. The french philosopher Michel Foucault (see Foucault 1968) assumes that such a classification is not a rational one and refers to a culture completely different from ours. In fact, we can only say that we are in front of a weak form of classification. However, it can be mathematically expressed, thanks to a model where classes overlap (Fig. 3). So, such a kind of organization is not irrational at all, and does not necessarily belong to some exotic epistéme.
So we must accept, as modes of organization, different types of classifications and many forms of orderings, sometimes weaker than hierarchies, sometimes more complex (like, for example, n-cubes). In this context, we decide to call classifications in a large sense structures such as systems of classes, partitions, hypergraphs, hierarchies or chains of partitions, semi-lattices, lattices, and so on. Moreover, all these structures may be crossed with another one, and may be also fuzzified.
4. Extensional structures
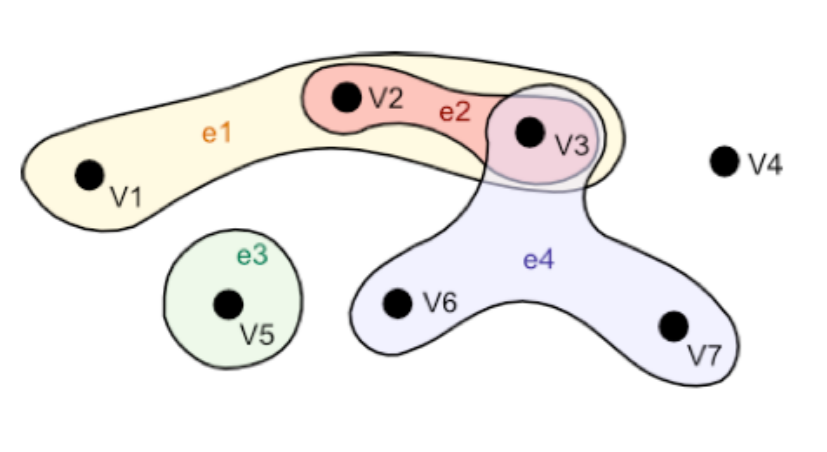
Let us now give true definitions of all the structures previously mentioned. We shall begin with structures associated to the weakest form of data organization and, from there, go to strong one: mathematics allow us to begin with very few axioms, that define weak general structures. Afterwards, by adding new conditions, we can get other properties and stronger models. In our case, the weakest structure is just a hypergraph, in the sense of Berge (1970).
4.1 From weak to strong structures
Let E be a nonempty finite set, P(E) the powerset of E. A hypergraph is a pair H = (E, P), where E is a set of vertices (or nodes) and P a set of nonempty subsets called (hyper)edges or links. Therefore, P is a subset of P(E)\∅. In such a structure, the set of edges does not cover the set X, because some node may have a degree zero, i.e. may have no link to some edge (see Fig. 4).
Now, suppose we add the following condition:
(C0) E ∈ P
In this case, we say that P is a cover (or covering) of the set of vertices E.
Assume now that, for every element, its singleton is in P. In symbols:
(C1) ∀x ∈ P, {x} ∈ P
then, we get a system of classes, in the sense of Brucker and Barthélemy (2007). Let us add now the new following conditions. For every ci belonging to P:
(C2) ci ∩ cj = ∅
(C3) ∪ci = E
Then P is a partition of E and the ci are the classes of the partition P (Fig. 5)

4.2. The lattice of partitions
Call now x P y, the relation "x belongs to the same class as y" and denote P(E) the set of partitions of a set E. A partition P is finer than a partition P' if x P y ⇒ x P' y. This relation allows us to define a partial order on P(E) that we shall denote P ≤ P'. We can see immediately that (P(E), ≤) is a lattice because (1) it is a partial order; and (2) moreover, every pair (P, P') has a greatest lower bound P ∧ P' and a least upper bound P ∨ P'. The first one is the discrete partition, whose classes are singletons. The second is the partition with one class, say E. One proves that P(E) is complemented, semi-modular and atomic (if the initial data E is a non atomic set, we can, under reasonable conditions, reduce the data to the atomic elements of E).
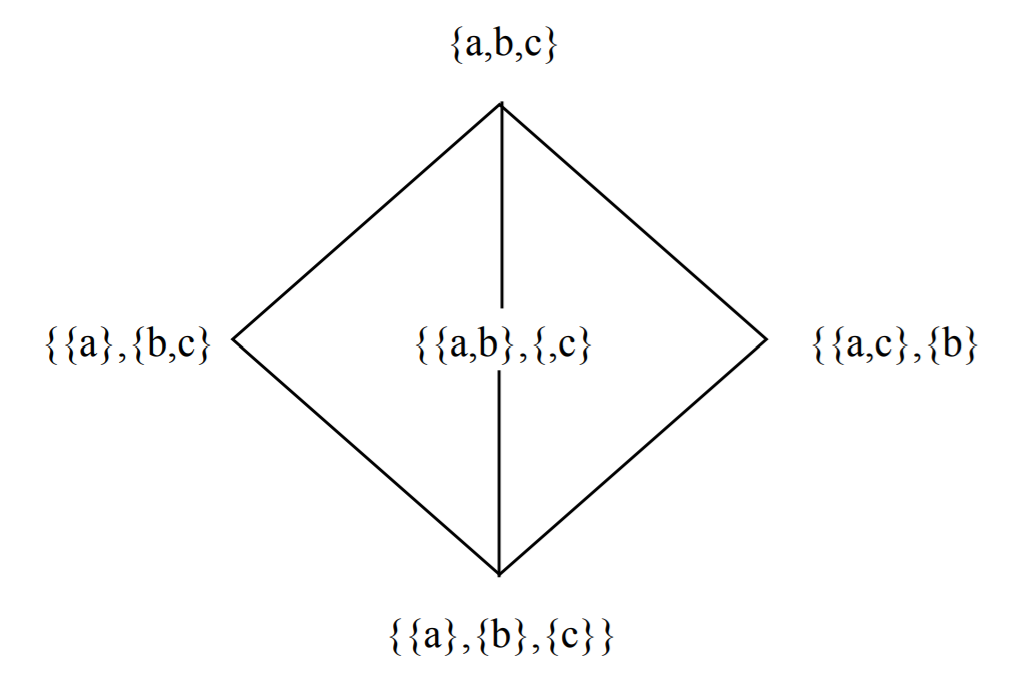
Example: The lattice of partitions for |E| = 3 (see Fig. 6):
In this context, a hierarchical classification, i.e a chain C of partitions of the lattice P(E), is a totally ordered subset of P(E). We have: C = {P1, P2, ..., Pn} with P1 < P2 < ... < Pn and:
Pi ∈ P(E)
Example : Correspondence between chains and hierarchical classifications (see Fig. 7):
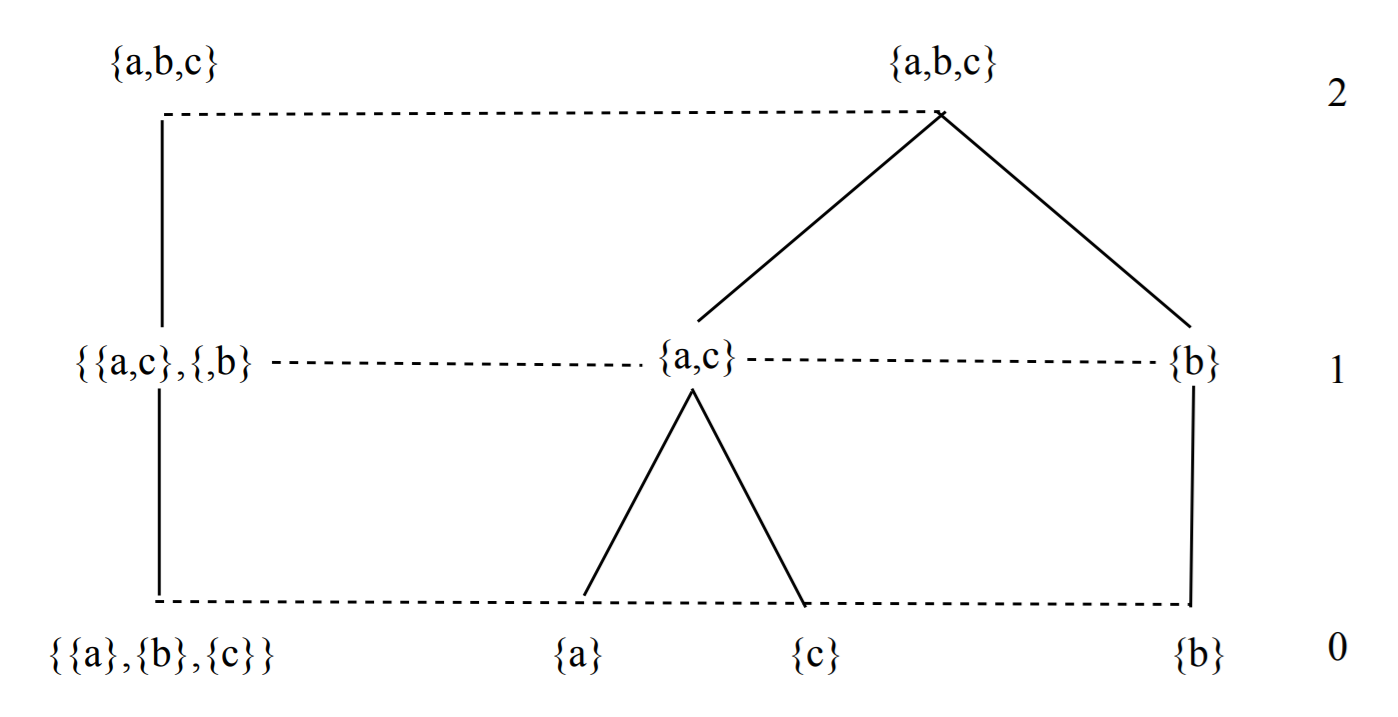
Note that the whole set of chains C(E) has itself a mathematical structure: it is a semilattice for set intersection.
This model allows us to get all the possible partitions of P(E) and all the possible chains of C(E). The problem is that the partitions are very numerous (Table 1).
| |E] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| |P(E)| | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 |
4.3 The case of covers
It is not very easy to examine which classification is the best one among, say, several thousands of them. The situation is worse with weaker structures like covers or even minimal covers. Recall that a family F of nonempty subsets of a set E, whose union contains the given set E (and which contains no duplicated subsets), is called a cover (or a covering) of E. A particular kind of cover is the minimal cover. A minimal cover is a cover for which the removal of one member destroys the covering property. Of course, we can make orderings on covers and build hierarchies of covers or minimal covers (Parrochia and Neuville 2013). But if the set L(E) of minimal covers is a lattice for the refinement relation, the set R(E) of all covers has no interesting properties: it is only a preorder (or a quasi-order) for the refinement relation (that we define in the same way as for the partition ordering). Moreover, computing the covers of a set leads immediately to big numbers (see Table 2). So it becomes rapidly impossible to examine the very numerous possible chains of covers.
| [E] | 1 | 2 | 3 | 4 |
| R(E) | 1 | 5 | 109 | 32297 |
5. Methods for building empirical classifications
How can we get classes, partitions, hierarchies, pseudo or quasi-hierarchies and so on? Generally, in the real world, the rough data presents itself as a non structured set E of objects (animals, plants, books, etc.) sharing (or not) some attributes or properties (shape, size, color, etc.). In order to make classes, we must first give a sense to the notion of similarity between two elements of E, the set of objects to be classified.
5.1. Distance, metric and ultrametric
We introduce first a mapping d, from E × E into ℝ+ which must satisfy some of the following axioms:
(1) d(x, y) = d(y, x)
(2) d(x, y) = 0 iff x = y
(3) d(x, z) = d(x, y) + d(y, z)
(4) d(x, z) = Max[d(x, y), d(y, z)]
If 1 and 2 are satisfied, d is a distance. If, moreover, 3 is satisfied, d is a metric. And if 4 is also satisfied, then d is an ultrametric. One proves (Lerman 1970; Benzécri 1973) that it is possible to associate an ultrametric with integer values to any chain of partitions. Now if d is an ultrametric on E, any function f(d) such that:
(1) f(0) = 0
(2) f(λd) > f(d) if λ > 1 and d ≠ 0
is also an ultrametric on E. A chain of partitions associated with an ultrametric d' = f(d), where d is the number of the partitions and f a monotonically increasing function, is named an indexed hierarchy. As said above, any ultrametric is associated with a matrix of distances: the distance between two elements x and y on the tree is the first level where the elements are in the same class. Of course, we have d(x,x) = 0 for all x and d(x,y) > 0 when x ≠ y. So we get a total equivalence between chains of partitions, ultrametrics and matrices of distances.
Example: The chain of partitions in Fig. 6 admits the matrix of distances of Table 3:
| a | b | c | |
| a | 0 | 2 | 1 |
| b | 2 | 0 | 2 |
| c | 1 | 2 | 0 |
Interpreted as an ultrametric matrix, a chain of partitions is the semi-ring
⟨R+∪{+∞},⊕,•⟩where ⊕ is interpreted by min and • by max (Gondran 1976). This structure is named dioid in Gondran and Minoux (2002). It may be transposed to the set of all ultrametric matrices (see also Gondran et Minoux 1979; 1984).
5.2. Algorithms for chains of partitions
In order to build concrete hierarchical classifications, we must first carefully define the objects to be classified; second, observe on any individual some variables from which we shall define a distance S(x, y) between them; third, define a new distance Δ(x, y) between the classes themselves, such that Δ(x, y) gives S(x, y) when those classes are reduced to one element. These tedious calculations are now carried out by computers. In the course of history, three kinds of methods held taxonomist's attention: hierarchical bottom-up methods, hierarchical top-down methods and, finally, non-hierarchical methods (for instance, aggregation around moving centroids). Hierarchical methods imply that relations between classes are ordered. Non hierarchical methods are only concerned with the construction of partitions where classes are unordered (so they keep away from the construction of actual classifications). Top-down methods are necessarily working according to independently specified criteria. Non-hierarchical methods do not use necessarily a notion of distance. Let us examine all that.
5.2.1. Bottom-up methods
Usually, one considers that bottom-up methods are those which give the best and most reliable results (Roux 1985). Let us see now how these last methods are working in the case of binary chains.
In such a case, we look for a pair (a, b) such that d(a, b) has the smallest value. We aggregate these two elements, that is, the first partition P1 is obtained from the discrete partition P0 by the operation:
P1 = [P0 - (a, b)] ∪ αwith:
α = a ∪ b
To any partition corresponds the aggregation of two particular subsets. This aggregation is represented by a node in the tree (associated with the chain of partitions). We denote n(α, β) the node corresponding to the aggregation of α and β. To any node may be associated an index I(n) = D(α, β). So we get an indexed hierarchy of partitions. In order to define the best among those partitions, one must define on them an objective function. Then we have to maximize the values of this function for all possible partitions, and finally choose the partition corresponding with the greatest value. But nothing assures us that all "optimal" partitions constitute a chain.
Many kinds of distances may be used (Lerman 1970; Parrochia and Neuville 2013, 79-80). But when we have a representation of the elements of E in the form of a cloud of points — each of them being assigned a certain weight and located in a metric space —, a center of gravity and an inertia can be calculated for each subcloud. It is then natural to look for pairs of points whose aggregation decreases the less the dispersion of the cloud, that is to say, its inertia. In this case, it is shown that the distance to be used is:
d2(x, y) = [mx my / (mx + my)] ||x - y||2
There exist also different strategies of aggregation (Roux 1985; Gordon 1996). For example: nearest neighbour method, diameter hierarchy, average distance. One of the most simple expressions of the average strategy is:
Δ(x,y) = (1 / CardX.CardY) ∑x∈X y∈Y{d(x,y)}
5.2.2.Top-down methods
This type of classification is performed by successive dichotomies, and so, at every step of the algorithm, there are two rules to be applied in order to determine (1) the choice of the class to split; (2) the objects assignment mode in each of the subclasses.
One of the oldest top-down algorithms is that of Williams and Lambert (1959), who choose to split the class with the largest number of objects. Others, like Hubert (1973), prefer dividing the class of larger diameter (remember that the diameter of a class is the distance between the two farthest points in it). None of the above processes is really justified and the right answer seems to be taking the class maximum dispersion. But many formulas can still express it.
5.2.3. Non-hierarchical methods
Non-hierarchical methods are particularly useful in classification problems of pattern recognition issues. In this domain, the main difficulty comes from our ignorance as to the underlying structure of the space. Should we make an assumption of separability, a probabilistic hypothesis, a metric hypothesis? One way to give an answer is to make a classification on a set T, called learning set, ignoring the actual forms ω1, ..., ωn. So one gets ω'1, ..., ω'p classes which are only neighboring of classes ω1, ..., ωn, in order that, in the ω'j classes, one ω'i class is dominant. There will be thus p ≥ n, and ω'1, ..., ω'p will be called recognizable forms. This classification, that can use several types of metrics, can therefore afford to make a realistic assumption about the structure of the space. The problem is then to use that structure for assigning an individual x to one of the ω'j classes.
5.2.3.1. k-means classifications
One example of this method is the k-means classification. It helps highlight nuclei A1, ..., Ap (symbolic description) for each of the recognizable forms ω'1, ..., ω'p and distances d(x, Aj) between individuals and nuclei. Nuclei acting as labeled and the distance d play the role of a membership function. So we are reduced to a fuzzy pattern recognition problem.
The k-means classification was introduced by MacQueen (1967). Other similar algorithms were developed by Forgey (1965) (see "mobile centers") or by Diday (1971) (see dynamic clouds method). This kind of methods has the following advantages: (1) an object can be assigned to a class during an iteration, then changes class to the next iteration. This is not possible with the hierarchical clustering, for which an assignment is irreversible; (2) by multiplying the starting points and repetitions, one can explore several possible solutions. The disadvantage of them is that they do not find out what can be a consistent number of classes, or how to visualize the proximity between classes or objects. The definition of an average between the data, as well as the calculation of the averages, which are very sensitive to outliers, are other limits of this model.
5.2.3.2. Other non hierarchical algorithms
In order to solve this last problem (the sensibility to outliers), other kinds of algorithms have been developed. One of them is the PAM-algorithm (partition around medioids) (Kaufman and Rousseuw 1990). In this method, each class is represented by one of its members named medioid, and not by a centroid, average of the set of its members. After a random choice of initial k medioids, the algorithm reviews all the pairs of individuals such as one is a medioid and the other not, evaluating whether the exchange of the two objects improves the objective function. In the end, the different objects are assigned to the closest medioid class. However, the renunciation of the centroids induces a certain algorithmic complexity and long computational times (each iteration is in O(k(n-k)2)). But it is possible to use some variant like CLARANS (Clustering large applications based upon randomized search) to reduce to a complexity in O(n).
Other methods based on the study of the dispersion of classes, on their density, on the quantification by grid, on the direct construction of dendograms complete the above possibilities. More recently, methods derived from biology (neural networks, genetic algorithms) or physics (super-paramagnetic clustering) have emerged, as well as methods for comparing these classifications (Boubou 2007).
Peano scans
Another type of non hierarchical method, sometimes useful in the domain of imagery, is the Peano scan, a general technique for continuous scanning of multidimensional data by a spacefilling curve (see Peano 1890). Hilbert (1891) presented a simplified version of Peano curves in terms of binary divisions (see examples of Hilbert (left) and Peano (right) curves of order 2 in Fig. 8), and then, generalized algorithms for images of arbitrary size have been invented by many authors.
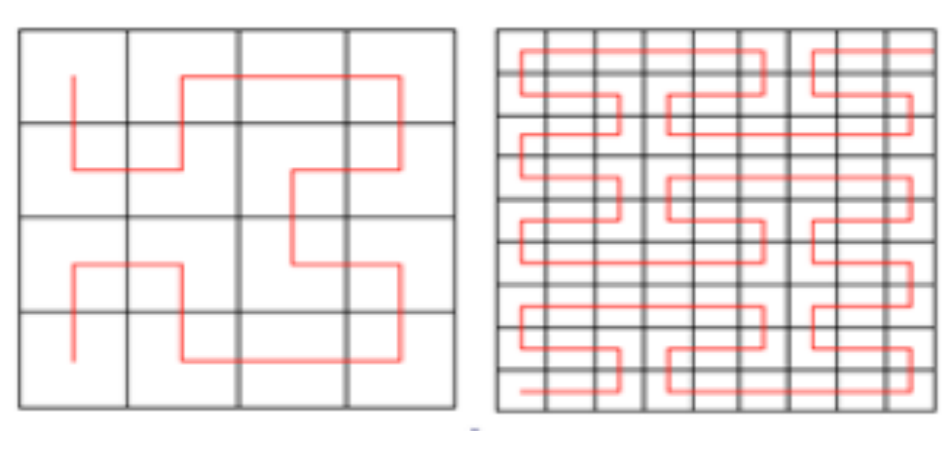
These methods immediately apply to classification. Let Rn be an n-dimensional space, i.e. an object represented by n measurements. Assume Rn is divided into rnp hypercubes H, r and p for varying accuracy. One sequentially explores these H with a Peano scan of order p. As we can define it now in a very general way, a Peano scan is indeed an addressing technique built by a recursive procedure on p. In this particular case, it is a technical addressing of the hypercube (1/rp)n with an address (k1, k2, ..., kn).
We may now define what is a rn neighbouring. Let H and H' be two hypercubes, whose respective addresses are (k1, k2, ..., kn) and (k'1, k'2, ..., k'n).
H and H' are rp-neighbors means
∑i |ki - k'i| ≤ 1
One shows that two Peano scans are sufficient to get the neigbourings and we do not need any kind of distance to build the classification.
5.3. Algorithms for covers and weak structures
Let Q be a cover on a set E and Qi ⊂ P(E) the powerset of E. Q is associated with the binary relation:
(∀x, y ∈ E) : xQy ⇔ x, y ∈ Qi
A cover Q is said to be finer than a cover Q' if:
xQy ⇒ xQ'yfor all x,y ∈ E.
Let us now define a sequence Q1, Q2, ..., Qh,... of covers on E, totally ordered by decreasing fineness. This sequence meets the similarities between objects if the first index h, for which any two given objects of E are combined in one part of Qh is even smaller than the similarity of the two objects is large. An algorithm built by Lerman (1970, 73) allows obtaining, naturally, a finite family of totally ordered sequences of covers. Each respects plainly, for a given degree of fineness, the similarities between objects.
Let ω be a preorder whose classes are B1, B2, ..., Bp. Assume we already got a chain of partitions (P0, P1, ..., Pq). To each partition Pi, we associate now a sequence of covers in the following way: for some h, a member of the cover Qh will be any class Eℓ of partitions Pi, or any class em of the partition corresponding to the cover of order h. Since, in practice, we are mainly interested in low-overlapping covers, Lerman proposes to determine, along with the previous sequence (P0, P1, ..., Pq), the sequence (Q11, Q12, ..., Q1q-1), the Q1i being defined from Pi and Bi. For example, suppose we got the following chain of partitions (P0, P1, P2, P3), with:
P0 = {{f}, {a}, {d}, {c}, {b}, {e}}
P1 = {{f}, {a, d}, {b, c}, {e}}
P2 = {{a, d, f}, {b, c, e}}
P3 = {{a, b, c, d, e, f}}
Let us remember that, in a chain of covers, the discrete cover is the discrete partition and the rough cover is the rough partition: so, only the intermediate levels are modified. In this example, we get:
Q11 = {{f}, {a, d, f}, {b, c}, {b, e}}
Q12 = {{a, d, f}, {b, c, e}, {d, e}}
5.4. Unsolved problems
Despite the fact that the previous methods are widespread, they are still not convincing because they lead to relatively unstable classifications. There are two kinds of instability: an intrinsic instability, due to the plurality of methods (distances, algorithms...) that can be used to classify the objects, and an extrinsic instability (our knowledge is changing), so the definitions of objects (or attributes) are evolving over time.
Intrinsic instability comes from the possibility of choosing different formulas for expressing the distance between objects and also different kinds of algorithms for aggregating classes. In general, the objects of the world have no ultrametric distances between them. The "rough data" is generally a numeric table which crosses objects and properties (predicates or attributes), these ones presenting sometimes different modalities. Objects can share some common properties, but they can also have specific ones. How may we choose a "good" formula to express this distance (or similarity measure)? In order to compare different similarity measures, Lerman (1970) defines the following variables:
- s: number of attributes which are common to the object x and to the object y (= what x and y are)
- t: number of attributes which are not possessed by x and by y (= what x and y are not)
- u: number of attributes possessed by the object x and not by the object y (= specificity of x)
- v: number of attributes possessed by the object y and not by the object x (= specificity of y)
- T: sum of all the attributes (T ≤ s + u + v).
Now a similarity measure is a function S, from E × E into ℕ3, such that, for all (x,y) of E × E, we have S(x,y) = S (s, u, v) ∈ ℕ3. The problem is that we can define S in many ways. In principle, to solve the problem, we would have to compare all the possible distances that can be chosen and measure the proximity of each of them to an ultrametric. Unfortunately, this is not possible, except for very small samples. So we are led to use approximative algorithms, which suppose, at their turn, new more or less arbitrary choices: nearest neighbour, diameter, average link, center of gravity, dispersion of elements within a class, etc. All that give at the end very different results, so the final classification is quite unstable.
Let us say now some words about extrinsic instability. This instability is due either to the quantitative variations of the populations of objects to be classified, or to the qualitative changes concerning the knowledge of their properties in the course of time. For instance, initial objects may be imprecise (Apostel 1963); new objects can also arrive (Lambert 1984) or old objects can disappear; moreover, unusual or strange objects ("monsters") may appear in the course of time (Dagognet 1970); finally, a discovery of new properties for some apparently well-known objects (resp. rejection of old ones) may also happen.
As an answer to intrinsic instability, Lerman (1970) proved that, if the number of attributes (or properties) possessed by the objects of a set E is constant, the associated quasi-order given by any "natural" metric is the same. But when the sample variance of the number of attributes is a big one, of course, the stability is lost. Similarly, if we classify the attributes, instead of classifying the objects, the reverse proposition is not true.
For extrinsic instability, the answers are more difficult to find. Of course, we may think to methods used in library decimal classifications (UDC, Dewey, etc.), which make possible infinite ramified extensions: starting with ten big classes, you divide each of them into ten more, and so on. Then, after having used integers, associated with the larger classes, it may be useful to introduce decimal points and to transform the first into decimal numbers. A decimal number being a periodic or aperiodic unlimited symbol, it is always possible to add new indices, and so, new classes, in the classification. But these classifications assume that higher levels are invariant and they have also the disadvantage to be enumerative and to degenerate rapidly into simple lists. Pseudo-complemented structures also exist (see Hillman 1965) with some kinds of waiting boxes (or compartments) for indexing things that have not yet been classified. We can get, as well, structures whose transformations obey certain rules that have been fixed in advance. That is the case of Hopcroft 3-2 trees, for instance (see Larson and Walden 1979). But these systems are not absolutely convincing: in both cases, the problem of justifying the underlying topology or the transformation rules remains unsolved.
As a consequence, the impossibility of solving the problem of instability of classifications invites us to look for some clear composition laws to be defined on the set of classifications over a set and to a good algebra of classifications, if it may exist one. This search is all the more crucial as a theorem proved by Kleinberg (2002) shows that one cannot hope finding a classifying function which would be together scale invariant, rich enough and consistent. This result explains that we cannot find, in fact, any empirical stable classification by using traditional clustering methods, even if computer science produces every year a lot of new algorithms or tries to solve the problem in many ways, including decompositions into subproblems supposed to lead to better approximations (Veloso and Meira 2011).
6. Intensional methods
Since its birth, classical logic has always admitted two types of interpretation: extensional and intensional. "All men are mortal" may mean in fact either that the class of men is contained in the class of mortals, or that the predicate of "mortality" is implied by the existence of the predicate of "humanity". For years, this question has divided the logicians, as evidenced by the numerous discussions between Plato and Aristotle, Pascal and Ramus, Jevons and Joseph, etc. More recently, the development of computer science brought this view back, since for declarative languages, and particularly object-oriented ones, pure extensional classes are rather uncommon. In this context, the preference is now given to the intensional approach.
In the intensional interpretation, a class is in correspondence with one or several properties which define its elements. Generally, the way the properties are found is not specified. It may be manually done or by using some technical approach like Galois lattice and conceptual analysis (Ganter and Wille 1999).
The requirements that must be satisfied to make a good (hierarchical) classification have been posed by Apostel (1963).
A division (or partition) is essential if there is no individual having one of the Qi-properties without having property P.
A classification is a sequence of implicative-disjunctive propositions: everything which has the property P also has one of the n properties Q1 ... Qn. Everything which has the property Qr also has the property S, and so on (Apostel 1963, 188).
A natural classification is such that the definition of the domain to be classified determines the criteria's choice of classification in a unique way.
The intensional weight w(P) of a property P is the set of properties' disjunctions that this property implies. A partition immediately follows another one if, for all P-properties of the first and all Q-properties of the second, disjunctively implied by these first, there are no properties R disjunctively implied by P and disjunctively implying Q.
An intensional optimal classification would have to satisfy the following requirements:
- Each level has a partition basis.
- No new partition basis is introduced before the previous one is depleted.
- Each partition is essential.
- The classification tree is regular.
- The succession of partitions is obvious.
In a natural intensional classification, scope definition to classify must determine in one and the same way the choice of classification criteria. Finally, the partition that immediately follows the trivial partition should be essential. The problem is: how to get essential partitions? How to obtain stable classifications, given the constant flow of information generated by an undefinitely growing knowledge?
7. Classifications and flows of information
During the 1970s, Barwise and Seligman (1997) wanted to create a new theory of information, involving the idea that information flow is made possible by regularities in systems. Rather than developing a machinery for analyzing those regularities, they built instead a mathematical theory based on their mere existence. The starting point is precisely the notion of classification, which thus appears in a new light. For the authors (see Devlin 2001), a classification is a structure A = ⟨A, ΣA,⊨ A⟩, where A is a set of objects to be classified, called the tokens of A. ΣA is a set of objects used to classify the tokens, called the types of A, and ⊨A is a binary relation between A and ΣA which determines which tokens are classified by which types. A familiar example to logicians is when the types are sentences of first-order logic and the tokens are mathematical structures, a ⊨ α being the relationship that the structure a is a model of the sentence α. The authors then develop a machinery for discussing the "logic" by means of which the system can support the flow of information.
What is intesting for us in this project is, first, the notion of informorphism the authors define between two classifications. For example, let A = ⟨A, ΣA,⊨ A⟩, and C = ⟨C, ΣC,⊨ C⟩ be two classifications. An infomorphism between A and C is a pair f = (f^, fv') of functions that makes the following diagram commute:
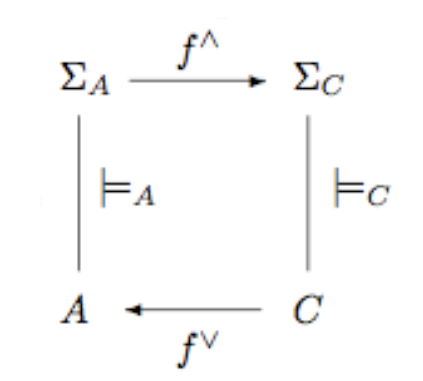
This means that for all tokens c of C and all types α of A:
fvfv(c) ⊨A α iff c ⊨C f^(α)
One usually refers to f^ as "f-up" and fv as "f-down". One takes account of the fact that the functions f^ and fv act in opposite directions by writing f: A ⇄ C. It may be the case, for example, of two mathematical theories.
Now an information channel consists of an indexed family C = {fi: Ai ⇄ C} i∈I of infomorphisms with a common codomain C, called the core of the channel. The intuition is that Ai are individual components of the larger system C, and it is by virtue of being parts of the system C that the constituents Ai can carry information about one another. Suppose A and B are constituent classifications in an information channel with core C. A token a being of type α in A carries the information that a token b is of type β in B relative to the channel C if a and b are connected in C and the translation of α entails the translation of β in Th(C) (Th(C) is the theory of the channel core). It is clear that the types in C provide the logical structure (the regularities) that gives rise to information flow, but information only flows in the context of a particular token c of C, i.e. a particular object.
Then, Barwise and Seligman make use of Category theory, and particularly of the notion of colimit, for getting a method for combining classifications. Given classifications A and B, one defines the colimit A+B as follows. The tokens of A+B consist of pairs (a, b) of tokens from each. The types of A+B consist of the types of both, except that, if there are any types in common, one must make two distinct (indexed) copies in order not to confuse them. There are natural infomorphisms σA: A ⇄ [A+B] and σB: B ⇄ [A+B] defined thus:
- σ^A(α) = αA (the A-copy of α), for each type α of A.
- σ^B(β) = βB, for each type β of B.
- For each token (a,b) of A+B, σvA((a,b)) = a and σvB((a,b)) = b.
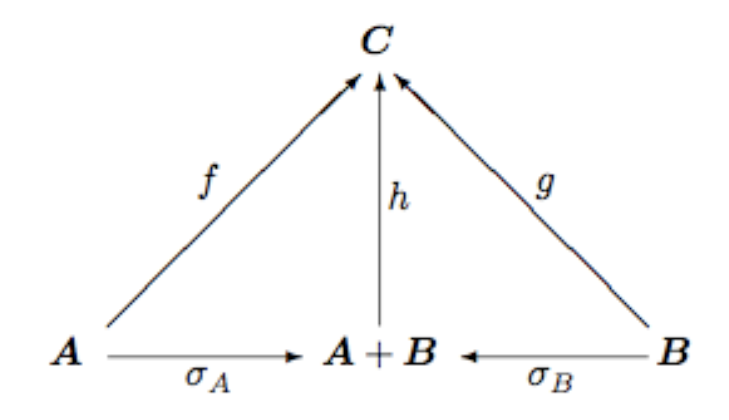
All that is good mathematics and explains well how information constraints may translate from a classification to another. However, it supposes we already get some classifications and have a complete theory of domain C. If not, the extended theory is more complicated. In this case, one must use a "local logic" to show how one can catch partial information. Then the theory explains more how the agents reason about information than how the real world actually works. It may be a complement for Shannon theory of information, but not a theory of classifications as such.
8. Towards a general theory of classifications
When we ask how to build good concrete classifications, the answer also is a mathematical approach to the problem. But the solution does not consist in using computers and running programs without thinking anymore. We have, before all, to get a sound mathematical basis in order to make stable classifications. To this aim, we can first take a glance at mathematical classifications themselves.
8.1. Classifications inside mathematics
Mathematics has dealt with classification for a long time. A quite common situation in this domain is: (1) the existence of a collection of objects X; (2) an equivalence relation ℛ on X. Now a complete classification of X up to ℛ consists of: (a) a set of invariants I; (b) a map c: X → I such that x ℛ y ⇔ c(x) = c(y). We can give a lot of examples where this method is working very well (the most famous case is the classification of finite semisimple groups into 17 infinite families plus the sporadic groups). Most often (Kechris 2001), the collection of objects to be classified may be viewed as forming a "nice" space, for example a standard Borel space. In this case, the theory of Borel equivalence relations allows us to study the set-theoretic nature of possible (complete) invariants and to develop a mathematical framework for measuring the complexity of classification problems. This way of approaching these problems in mathematics has become, for some years, a new area under active investigation. The question of cataloging a class of mathematical objects up to some notion of equivalence by invariants, and the closely related theory of descriptive dynamics, i.e., the theory of definable actions of Polish groups on Polish spaces, have been developed by several authors in a very promising manner (though some impossibile results have been encountered in a few cases). Of course, by the means of category theory and automorphism groups, we can always find a very general method to compare mathematical structures, and so, we should be theoretically able to classify a lot of them (groups, rings, matrices, etc.), as Pierce (1970) has already shown. However, in the details, many problems raise, especially concerning big collections of very general structures (graphs, fields, varieties and so on). One could think it is possible to turn around the problem in using logic. Generally speaking, mathematical structures satisfy some axiomatics and, as such, may be described as logical theories. Model theory — and in model theory, particularly the so-called "classification theory" created by Shelah (1978) — tries to classify those abstract logical theories by studying the relations existing between them and their mathematical interpretations (or models). But, to pursue this aim, classification theory must often deal with an infinite number of structures, and the way the infinite is defined takes a great importance and very much influences the results we get in the end. Moreover, some theories cannot be classified at all, because they are not stable and have not good structure theorems.
8.2 Searching for an algebra of classifications
So we need an algebra of classifications, which can explain all their transformations. The problem is that such an algebra should be:
- commutative (if a and b are classes, a • b = b • a);
- nonassociative (if a • (b • c) is a classification, (a • b) • c is not the same classification). So we have necessarily: a • (b • c) ≠ (a • b) • c.
This recalls nonassociative products of Wedderburn-Etherington (see Comtet 1970). We can improve this notation by suppressing parentheses if we write for instance bc•a• instead of a • (b • c) (Reverse Polish Notation or RPN invented by Lukasiewicz in the 1920s). Let us give some examples of classifications written in RPN. In words, we have:
a, ab•, ab•c•, ab•cd••, abc••de••.Here are the corresponding diagrams (see Fig. 9).
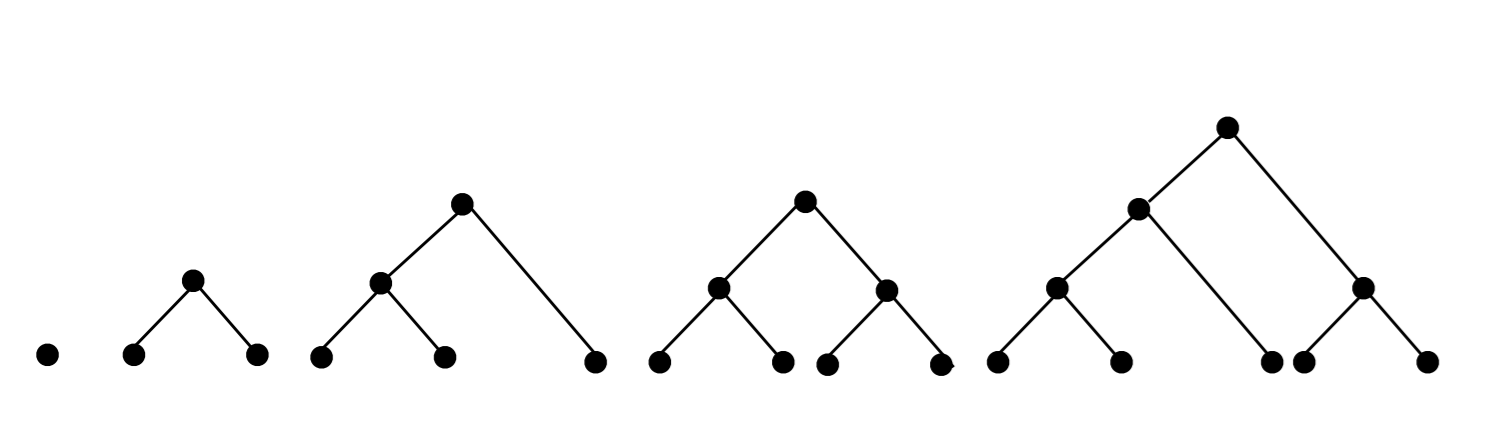
We get the following results (Parrochia and Neuville 2013):
Proposition 1 (RPN-classification correspondence): A classification can be attached to each RPN sentence but the reverse is false.
Proof: To prove this, it is sufficient to choose a classification whose partitions are not covering themselves. For instance, let C ={(abcde), (a, bcd, e), (a, b, c, d, e)}. There is no RPN sentence for such a classification. (As usual, in order to simplify writing, we have replaced {{a},{b},{c}} with (a, b, c).)
Definition 1 (notion of magma): Let E be a set of variables, representing classes. Let • be an internal law of composition, i.e a mapping from E × E into E. According to Bourbaki, (E,•) is a magma.
Proposition 2 (classification as a magma): Each classification (written in RPN) is a commutative and non associative magma:
(1) a ∈ E, b ∈ E, a • b = b • a (commutativity);
(2) a ∈ E, b ∈ E, c ∈ E: (a • b)•c ≠ a •(b • c) (non associativity).
This structure can be extended to the set of all classifications over a set (which is also a non associative magma).
Proposition 3 (isomorphic classifications): Two classifications with n elements are isomorphic if their connectors are located in the same place (when we use RPN notation).
Example: ab•c• and b•ac• are obviously isomorphic.
Definition 2 (extension of a classification): A classification A with n elements extends a classification B with p elements if B is included in A.
Example: ab•c•d• extends ab•c•.
We need an algebra of classifications because we would like to combine classifications between themselves and to generate complex classifications from more simple ones — as Barwise and Seligman do in the case of information flows. The problem is that the compound of two classifications is not necessarily a classification, because the order structure on the levels may be lost when we go from one to the other.
Intuitively, in order to be joined with a classification C1, a classification C2 may have a structure which, even if it extends the structure of C1, however, must also respect this very structure. So, the operation ⊕ may be admitted as an internal composition law only if C3 = C1 ⊕ C2 remains a classification. To express that, we need a particular algebra. But it is not, in fact, easy to find.
8.3. Some candidates among the algebras
As we have seen, an algebra of classifications should be commutative and non associative. But there are very few algebras like that. Indeed, most of the algebraic structures are associative ones. Getting such an algebra is a very difficult problem and it is the reason why, for the moment, we get only some candidates but no real answer. Among the well-known existing algebras, we have: K-algebras, Hopf algebras, dendriform algebras, right-symmetric algebras, etc. Some of them are working well on trees, but not necessarily on classification trees. For example, that is the case of the Dzhumadil'daev and Löfwall algebra (2002): most of the time, we cannot interpret its tree combinations in the view of taxonomic transformations. However, more recently, Drensky and Holtkamp (2008) have connected trees, nonassociative algebras and K-algebras. More precisely, they described free nonassociative algebras in terms of labeled reduced planar rooted trees — an approach that can certainly be applied to classifications.
8.4 A common construction for tree-like classifications and hypercube-like classifications
Instead of the missing algebra of classifications, let us introduce some elements of graph theory. As Mulder (2016) shows, the simplest way to obtain a tree from a smaller one is by adding a pendant vertex (a vertex of degree 1). Suppose we can cover a tree-like classification C with two subtree-like classifications C*1 and C*2 that have exactly a vertex in common. To obtain a larger (tree-like) classification, we take two disjoint copies of these (subtree-like) classifications C1 and C2, as shown in Fig.7 (right), then join the vertices in these subtree-like classifications that correspond to the common vertex in C*1 and C*2. We obtain an expansion with respect to the covering tree-like classifications C*1, and C*2 (see Fig. 10).
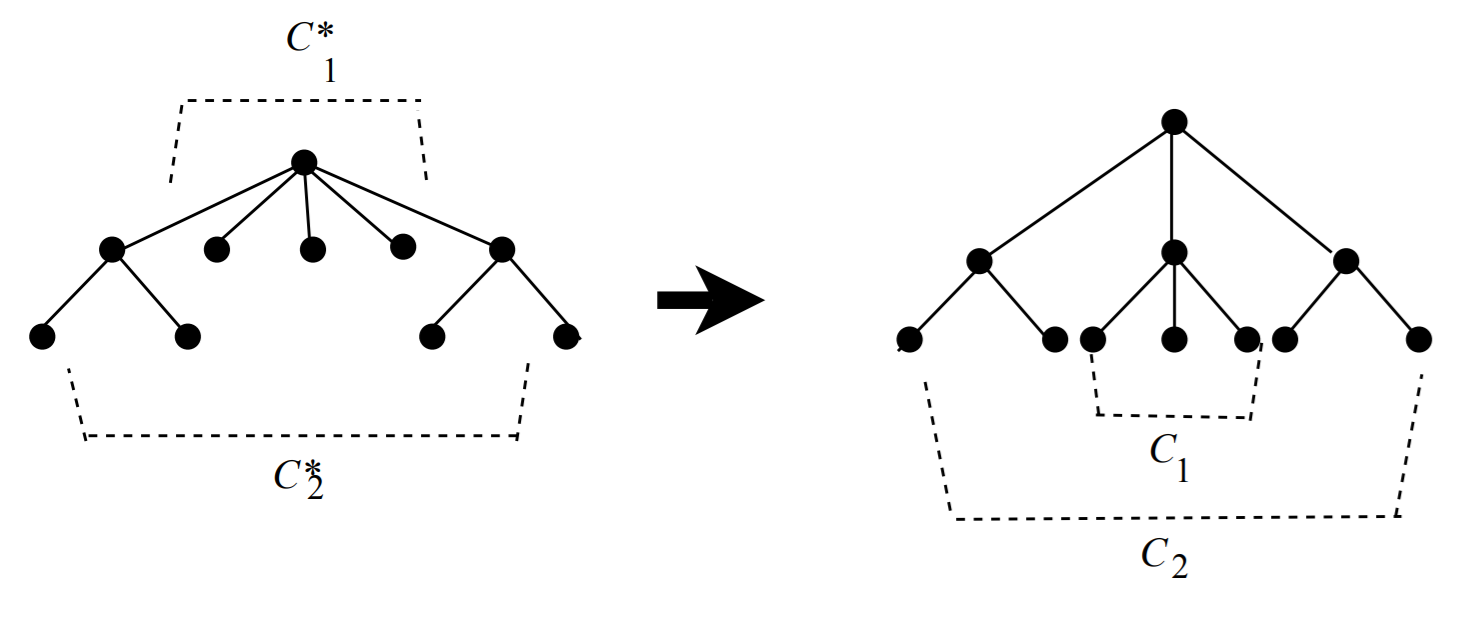
Each tree-like classification can be obtained by a succession of such expansions from the one-vertex graph K1. But we also know that hypercubes can be obtained in a similar manner by expansion, as depicted in Fig. 11.
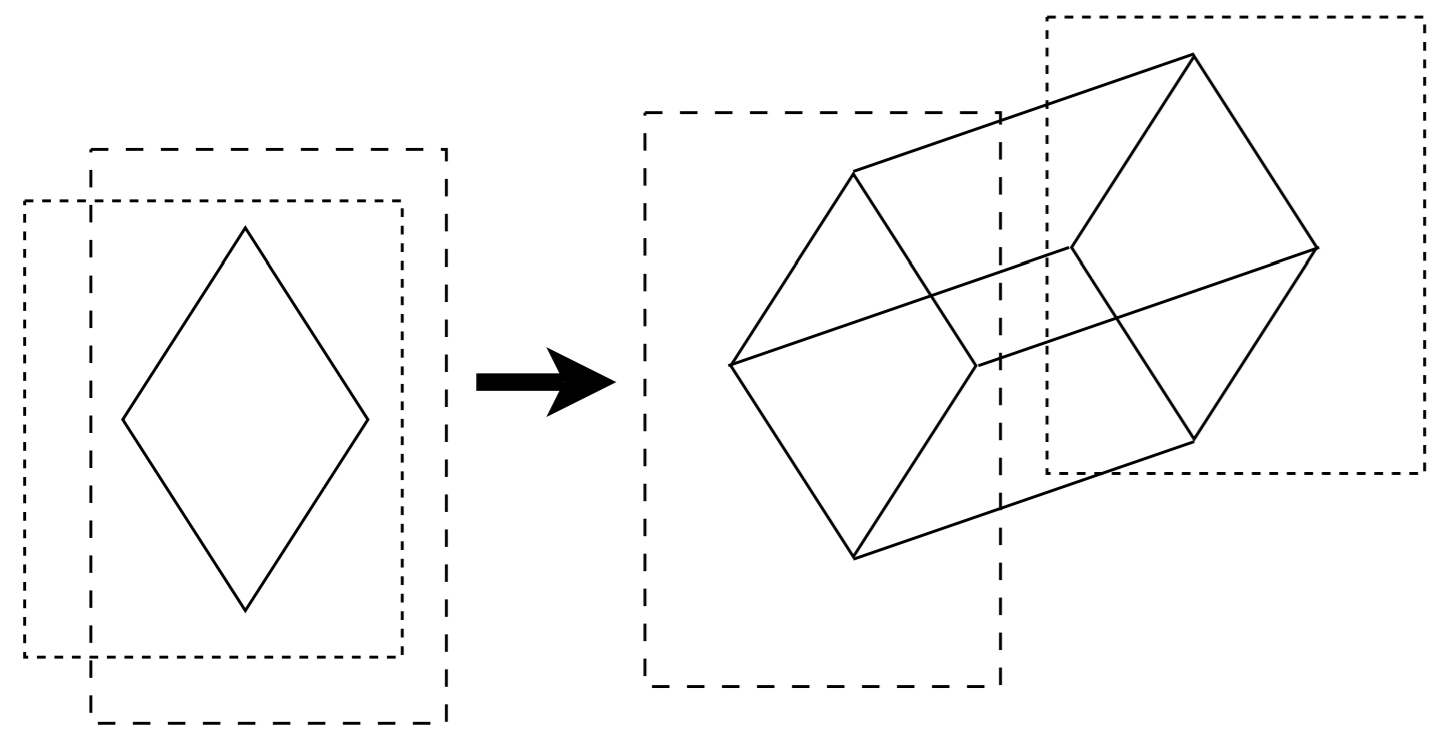
One covers the n-cube on the left by two subcubes, both of which equal to the whole n-cube. One takes two disjoint copies of these two subcubes and join respective vertices in the two copies. Thus one gets a hypercube of dimension n+1. Every hypercube can also be obtained by a finite sequence of such expansions, starting from the one-vertex graph K1. So this construction is a common property of tree-like classifications and hypercube-like classifications. We shall not give its true formalization although that can be rigorously expressed (see Mulder 2016, 155-156).
9. Conclusion
9.1. The missing theory
At present time, a general algebra of classifications on a set is not known. However, we are invited to search it, for two reasons: (1) the world is not completely chaotic and our knowledge is evolving according to some laws ; (2) there exists, for sure, quasi-invariant classifications in physics (elementary particle classification), in chemistry (Mendeleev table of elements), in crystallography (the 232 crystallographic groups), etc. Most of these "good" classifications are founded on some mathematical structures (Lie groups, discrete groups, etc.). It is therefore not absolutely unrealistic to think that the "dream" of a general theory for classifications will come true, as anything that has a structure can be explained mathematically.
9.2. A philosophical view
To sum up the question of a classification theory, we may propose the following scheme (see Fig. 12), that we comment below:
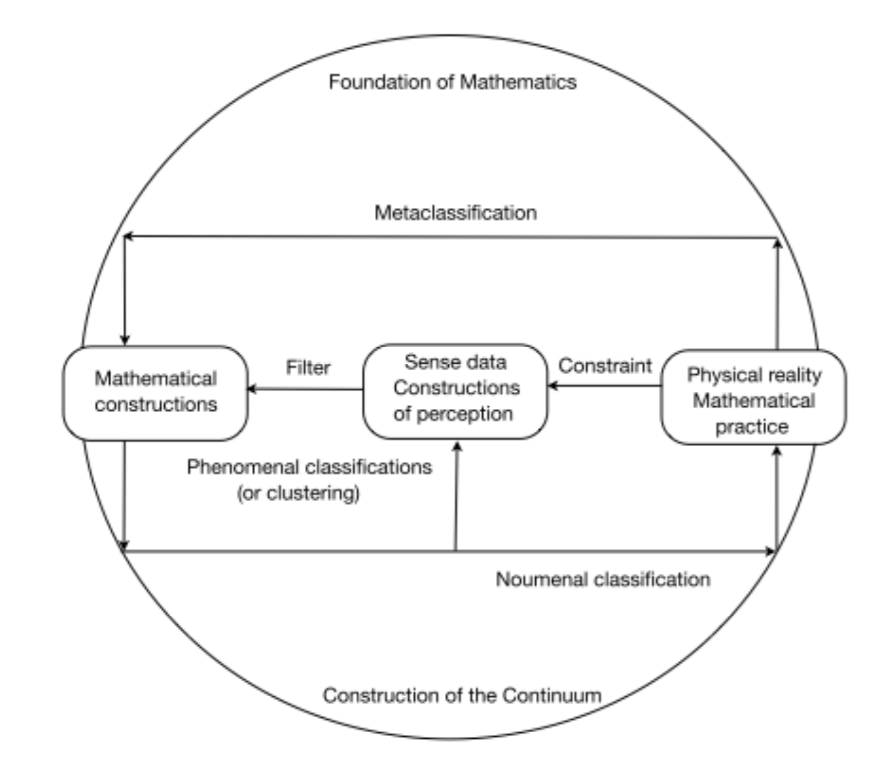
(1) When our mathematical tools apply to sense data, we get only phenomenal classifications (by clustering methods).
(2) When our mathematical tools deal with crystallographic or quantum structures, we get noumenal classifications (for instance, by invariance of discrete groups or Lie Groups). Of course noumenons never give "things in themselves". Even for Immanuel Kant, they are only negative or problematic ideas (see Kant 1998, 348-9). Let us recall that, for Kant, a noumenon would be the idea of the thing in itself, if this idea existed. But it does not exist, at least in a positive form. However, the French philosopher Gaston Bachelard (1936) has further weakened this Kantian notion of noumenon in that of metric noumenon, i.e a noumenon relating to the power of our scientific instruments, or more generally, to the power of our theoretical knowledge: Gaston Bachelard (1933, 140) himself used to say that, very often, a scientific instrument is but a reified theorem. Therefore by "noumenal classifications" we mean those classifications that are based on mathematical structures and robust assumptions of our theoretical knowledge.
(3) When we look for a general theory of classifications (finite and infinite), we are in the domain of pure mathematics and face the problem of the construction of the continuum: for example, under the Continuum Hypothesis, one proves that the infinite set of partitions P(E), defined on a countable set E, is an uncountable set with the same cardinality as ℝ, the set of real numbers. But other hypotheses can be admitted, and there are many ways in mathematics to see the Continuum and to perform its construction.
9.3 Final remarks: from continuum to empirical data
Today, many have forgotten that Cantor's mathematical research on the sets of points debouched on a conception of matter and a classification of everything which was intended as a general theory of the construction of events. His aim was to build a kind of mapping between mathematical elements and natural phenomena through the concept of the power of a set (see Cantor 1885, reprinted in Cantor 1932 and a letter from Cantor to Mittag-Leffler: Meschkowski 1967).
At present, of course, we cannot accept Cantor's ideas on classification of natural phenomena anymore. However, it still exists a natural correspondence between mathematics and concrete classifications. A well-known example is Fisher's data set, collecting the morphologic variation of Iris flowers of three related species: Iris setosa, Iris virginica, and Iris versicolor (Fisher 1936). It shows that the length (L) and width (W) of sepals and petals, measured in centimetres, were sufficient to classify Iris flowers. If L < 2,45, then they belong to I. setosa. If not, one considers W. If W < 1,75, then the Iris is versicolor. If not, it is virginica. Crucial values of L (2,45) or W (1,75) are real numbers and also indices of classifications.
A recent conjecture (see Parrochia and Neuville 2013) is that all classifications on a set (represented by non-intersecting ellipsoids in a n-space) are convergent in one and the same point, which is the index of the classification. So, without any additional hypothesis, the infinite set of all classifications is but the continuum of the real line.
References
Adanson, Michel. 1763. Familles des plantes. Paris: Vincent.
Aho, Alfred V., Hopcroft, John E. and Ulmann, Jeffrey D. 1983. Data structures and algorithms. Reading (Mass.): Addison-Wesley Publishing Company.
Alexander, Christopher. 1965. "A city is not a tree". Architectural Forum 122, no. 1: 58-61, and no. 2: 58-62.
Apostel, Leo. 1963. "Le problème formel des classifications empiriques". In La classification dans les sciences, publié avec le concours du Centre national de recherches de logique et de la Société belge de logique et de philosophie des sciences. Gembloux: J. Duculot, 157-230.
Bachelard, Gaston, 1933/2016. Les intuitions atomistiques: essai de classification. Paris, Boivin. Reprinted Paris: Vrin, 2016.
Bachelard, Gaston. 1936/1970. "Critique préliminaire du concept de frontière épistémologique". In Actes du VIII Congrès international de philosophie, à Prague (2-7 septembre 1934), Prague, Orbis, 1936: 3-9. Reprinted in G. Bachelard, Etudes, Paris: Vrin 1970.
Barbut, Marc and Bernard Montjardet. 1971. Ordre et classification: algèbre et combinatoire, tome 1-2. Paris: Hachette.
Barwise, Jon and Jerry Seligman. 1997. Information flow: the logic of distributed systems. Cambridge: Cambridge University Press.
Benzécri, Jean-Paul. 1973. L'analyse des données, Tome 1: la Taxinomie; Tome 2: L'analyse des correspondances. Paris: Dunod.
Berge, Claude. 1970. Graphes et hypergraphes. Paris: Dunod.
Birkhoff, Garrett. 1935. "On the structure of abstract algebras". Proceedings of the Cambridge Philosophical Socciety 31, 433–54.
Birkhoff, Garrett. 1949. "Théorie et application des treillis". Annales de l'Institut Henri Poincaré 11, no. 5: 227–40.
Birkhoff, Garrett. 1967. Lattice theory. 3rd ed. Providence: American Mathematical Society.
Borges, Jorge Luis. 2001. "John Wilkins' analytical language". In Eliot Weinberger, The total library: non-fiction 1922–86. London: Penguin Books, 229–232.
Boubou, Mounzer. 2007. Contribution aux méthodes de classification non supervisée via des approches prétopologiques et d'agrégation d'opinion. Thèse, spécialité: Statistiques-informatique, Université Lyon I, France. (Dissertation).
Bourbaki, Nicolas. 1959. Théorie des ensembles. Paris: Hermann.
Brucker, François and Jean-Pierre Barthélemy. 2007. Eléments de classification: aspects combinatoires et algorithmiques. Paris: Hermes Science.
Candolle, Augustin Pyramus de. 1813. Theorie èlementaire de la botanique, ou Exposition des principes de la classification naturelle et de l'art de décrire et d'étudier les végétaux. Paris: Déterville.
Cantor, Georg, 1885/1932. "Über verschiedene Theoreme aus der Theorie der Punktmengen in einem n-fach ausgedehntern stetigen Raumen Gn". Zweite Mitteilung, Acta mathematica 7, no. 8, 105-124 (1885), rep. in Georg Cantor, Gesammelte Abhandlungen mathematischen und philosophishen Inhalts, Berlin: Springer, 1932, 261-77.
Comte, Auguste. 1830/1975. "Philosophie première". Cours de philosophie positive, leçons 1–45 (1830). Reprinted Paris, Hermann, 1975.
Comtet, Louis. 1970. Analyse combinatoire. Paris: Presses Universitaires de France.
Dagognet, François. 1970. Le catalogue de la vie: étude méthodologique sur la taxinomie. Paris: Presses Universitaires de France.
Dahlberg, Ingetraut. 2014. Wissensorganisation: Entwicklung, Aufgabe, Anwendung, Zukunft. Würzburg: Ergon Verlag.
Devlin, Keith. 2001. The Mathematics of Information, Lecture 4: Introduction to Channel Theory. Helsinki: ESSLLI.
Diday, Edwin. 1971. "Une nouvelle méthode en classification automatique et reconnaissance des formes: la méthode des nuées dynamiques". Revue de statistique appliquée 19, no. 2: 19-33.
Drensky, Vesselin and Ralf Holtkamp. 2008. "Planar trees, free nonassociative algebras, invariants, and elliptic integrals". Algebra and Discrete Mathematics 7, no. 2: 1-41.
Drouin, Jean-Marc. 1994. "Classification des sciences et classification des plantes chez Augustin-Pyramus de Candolle". Revue de Synthèse IVe S, nos. 1-2: 149-65.
Drouin, Jean-Marc. 2001. "Principles and uses of taxonomy in the works of Augustin-Pyramus de Candolle". Studies in history and philosophy of science, Part C 32, no. 2: 255-75.
Dubreil, Paul and Marie-Louise Dubreil-Jacotin. 1939. "Théorie algébrique des relations d'équivalence". Journal de mathématiques 18: 63–95.
Dzhumadil'daev, Askar and Clas Löfwall. 2002. "Trees, free right-symmetric algebras, free Novikov algebras and identities". homology, homotopy and applications 4, no. 2: 165-90.
Everitt, Brian S., Sabine Landau and Morven Leese. 2001. Cluster analysis. 4th ed. London: Arnold.
Fisher, Ronald Aylmer. 1936. "The use of multiple measurements in taxonomic problems". Annals of human genetics 7, no. 2, 179–88.
Forgey, Edward W. 1965. "Cluster analysis of multivariate data: efficiency versus interpretability of classifications". Biometrics 21: 768-9. (Meeting abstract).
Foucault, Michel. 1968. Les mots et les choses. Paris: Gallimard.
Ganter, Bernhard and Rudolf Wille. 1999. Formal concept analysis: mathematical foundations. Berlin: Springer-Verlag.
Girard, Jean-Yves. 1987. Proof theory and logical complexity Volume 1. Napoli: Bibliopolis.
Gondran, Michel. 1976. "La structure algébrique des classifications hiérarchiques". Annales de l'INSEE 22-23, 181-190.
Gondran, Michel and Michel Minoux. 1979. Graphes et algorithmes. Paris: Eyrolles.
Gondran, Michel and Michel Minoux. 1984. Graphs and algorithms. New York: John Wiley and Sons.
Gondran, Michel and Michel Minoux. 2002. Graphes, dioïdes et semi-anneaux: nouveaux modèles et algorithmes. Paris: Tec et Doc-Lavoisier.
Gordon, Allan D., 1996. "Hierarchical classification". In Phipps Arabie, Lawrence J. Hubert, and Geert de Soete (eds.), Clustering and classification. Singapore: World Scientific, 65-121.
Hilbert, David. 1891. Ueber die stetige Abbildung einer Linie auf ein Flikhenstuck. Mathematische Annalen 38: 459-460.
Hillman, Donald J. 1965. Mathematical Classification Techniques for Non-static Document Collections, with Particular Reference to the Problem of Relevance. In Pauline Atherton (ed.), Classification Research: Elsinore Conference Proceedings, Copenhagen: Munksgaard, 177-209.
Hjørland, Birger. 2017. "Classification". Knowledge Organization 44, no. 2, 97-128. Also available at: https://www.isko.org/cyclo/classification.
Hubert, Lawrence J. 1973. "Monotone invariant clustering procedures". Psychometrika 38: 47-62.
Jambu, Michel and Marie-Odile Lebeaux. 1978. Classification automatique pour l'analyse des données, Volume 2, Logiciels. Paris: Dunod.
Kant, Immanuel. 1800/1963. Introduction to logic. New York: Philosophical Library, 1963. (German original: Gottlob Benjamin Jäsche (ed.). Immanuel Kants Logik: ein Handbuch zu Vorlesungen, Königsberg: F. Nicolovius, 1800).
Kant, Immanuel. 1781/1998. Critique of pure reason. Cambridge: Cambridge University Press.
Kaufman, Leonard and Peter J. Rousseuw. 1990. Finding groups in data: an introduction to cluster analysis. New York: John Wiley and Sons.
Kechris, Alexander S. 2001. Actions of Polish groups and classification problems. Analysis and logic: London Math. Soc. lecture note series, Cambridge: Cambridge University Press.
Kleinberg, Jon. 2002. "An impossibility theorem for clustering". Advances in neural information processing systems (NIPS) 15: 446-53.
Krasner, Marc, 1944. Nombres semi-réels et espaces ultramétriques. Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences 219, no. 2: 433-5.
Kurepa, Georges. 1935. Ensembles ordonnés et ramifiés. Belgrade: Publications Mathématiques de l'Université de Belgrade 4. (Thesis présenté a la Faculté des Sciences de l'Université de Paris).
Lamarck, Jean-Baptiste de. 1801. Système des animaux sans vertèbres ou Tableau général des classes, des ordres et des genres de ces animaux. Paris: Déterville.
Lambert, Jacques. 1984. "Classer vaut pour découvrir, coder vaut pour inventer". In Francois Dagognet (ed.) Anatomie d'un épistémologue. Paris: Librairie Philosophique J. Vrin, 23-35.
Larson, James A. and William E. Walden. 1979. "Comparing insertion schemes used to update 3-2 trees". Information systems 4: 127-36.
Lerman, Israël César. 1970. Les bases de la classification automatique. Paris: Gauthier-Villars.
Lerman, Israël César. 1981. Classification et analyse ordinale des données. Paris: Dunod.
Linnaeus, Carl. 1758. Systema Naturae per regna tria naturae, secundum classes, ordines, genera, species, cum caracteribus, differentiis, synonymis, locis, vol. 2. 10th edition. Holmiae: Impensis direct. Laurentii Salvi.
Luszczewska-Romahnowa, Seweryna and Tadeusz Batóg. 1965a. "A generalized classification theory I", Studia logica XVI: 53–70.
Luszczewska-Romahnowa, Seweryna and Tadeusz Batóg. 1965b. "A generalized classification theory II", Studia logica XVII: 7–30.
MacQueen, James B. 1967. "Some methods for classification and analysis of multivariate observations". Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probabilty 1: 281-97. University of California Press.
Meier, Andreas, Günter Schindler and Nicolas Werro. 2008. "Fuzzy classification on relational databases". In José Galindo, Handbook of research on fuzzy information processing in databases volume 2. Hershey: Idea Group Publishing, 586-614.
Mendeleev, Dimitri, 1869. "The dependence between the properties of the atomic weights of the elements". Zeitschrift für Chemie, 404-405.
Meschkowski, Herbert. 1967. Probleme des Unendlichen, Werk und Leben Georg Cantors. Berlin: Springer Verlag.
Mulder, Henry Martyn. 2016. "What do trees and hypercubes have in common?" In Ralucca Gera, Stephen Hedetniemi and Craig Larson (eds.), Graph theory, favorite conjectures and open problems I, Cham: Springer-Verlag International, 149-70.
Neuville, Pierre. 1984. Vers des formalisations algébriques pour les classifications. Lyon: ENSSIB.
Ore, Oystein. 1942. "Theory of equivalence relations". Duke Mathematical Journal 9, no. 3, 573–627;
Ore, Oystein. 1943. "Some studies on closure relations". Duke Mathematical Journal 10, no. 4, 761–85.
Parrochia, Daniel 2016. "Classification". In James Fieser and Bradley Dowden eds., The Internet encyclopedia of philosophy. Martin, TN: University of Tennessee at Martin. http://www.iep.utm.edu/classifi/
Parrochia, Daniel and Pierre Neuville. 2013. Towards a general theory of classifications. Basel: Birkhäuser.
Pawlak, Zdzislaw. 1982. "Rough sets". International Journal of Parallel Programming 11, no. 5: 341–56.
Peano, Giuseppe. 1890. "Sur une courbe, qui remplit toute une aire plane". Mathematische Annalen 36, no. 1: 157-60.
Pierce, Russell Stewart. 1970. "Classification problems". Mathematical System Theory 4, no. 1: 65-80.
Rasiowa, Helena. 1974. An algebraic approach to non-classical logics. Amsterdam: North Holland.
Riordan, John. 1958. Introduction to combinatorial analysis. New York: Wiley.
Roux, Maurice. 1985. Algorithmes de classification. Paris: Masson.
Shelah, Saharon. 1978. Classification theory and the number of non-isomorphic models. Amsterdam: North Holland. 2nd ed. 1990.
Sokal, Robert R. and Peter H. A. Sneath. 1973. Principles of numerical taxonomy. San Francisco: Freeman.
Sierpinski W. 1920. "Sur la décomposition des ensembles de points en parties homogènes". Fundamenta Mathematicae 1: 28-34; reprinted in W. Sierpinski, Œuvres choisies, tome 2, Editions scientifiques de Pologne, Warzawa, 1973, 303-7.
Veloso, Adriano and Wagner Meira Jr. 2011. Demand-driven associative classification. Dordrecht: Springer Verlag.
Williams, William Thomas and Joyce M. Lambert. 1959. "Multivariate methods in plant ecology, I: Association-analysis in plant communities". Journal of Ecology 47, no. 1: 83-101.
Zadeh, Lotfi A. 1965. "Fuzzy sets". Information and Control 8, no. 3: 338–53.
Visited
times since 2018-04-17 (10 months after first publication).
Version 1.2 (= 1.0 plus abstract, reference to Adanson 2763 and many minor corrections); published 2017-06-20, this version 2019-06-06
Article category:
Methods, approaches & philosophiesThis article (version 1.0) is published in Knowledge Organization, vol. 45 (2018), Issue 2, pp. 184-201.
How to cite it (version 1.0): Parrochia, Daniel. 2018. “Mathematical theory of classification”. Knowledge Organization 45, no. 2: 184-201. Also available in Hjørland, Birger, ed. ISKO Encyclopedia of Knowledge Organization, https://www.isko.org/cyclo/mathematical_theory_of_classification
©2017 ISKO. All rights reserved.