I S K O
Encyclopedia of Knowledge Organization
Hierarchy
by Michael K. BergmanTable of contents:
1. Introduction
2. Etymology and history
3. Perspectives on knowledge hierarchies
3.1 Theories of hierarchy
3.2 Hierarchical objects and relations
3.3 Subsumption in knowledge representation
4. Insights from Peirce
4.1 Peirce, the classifier
4.2 Trichotomies in logic, signs, and reality
4.3 Fallibility, the scientific method, and pragmatism
5. A typology of knowledge system hierarchies
6. Conclusion
Acknowledgments
Endnotes
References
Appendix: Some definitions related to hierarchy in ISO standards
ColophonAbstract:
Hierarchies — real or artificial — abound to help us organize our world. A hierarchy places items into a general order, where more ‘general’ is also more ‘abstract’. The etymology of the word hierarchy is grounded in notions of religious and social rank. This article, after a broad historical review, focuses on knowledge systems, an interloper of the term hierarchy since at least the 1800s. Hierarchies in knowledge systems include taxonomies, classification systems, or thesauri in library and information science, and systems for representing information and knowledge to computers, notably ontologies, knowledge graphs, and knowledge representation languages. Hierarchies are the logical underpinning of inference and reasoning in these systems, as well as the scaffolding for classification and inheritance. Hierarchies in knowledge systems express subsumption relations that have many flexible variants, which we can represent algorithmically, and thus computationally. This article dissects the dimensions of that variability, leading to a proposed typology of hierarchies useful to knowledge systems. The article argues through a perspective informed by Charles Sanders Peirce that natural hierarchies are real, can be logically determined, and are the appropriate basis for knowledge systems. Description logics and semantic language standards such as RDF or OWL reflect this perspective, importantly through their open-world logic and vocabularies for generalized subsumption hierarchies. Recent research suggests possible mechanisms for the emergence of natural hierarchies involving the nexus of chance, evolution, entropy, free energy, and information theory.
1. Introduction
Humans have a propensity to organize and categorize things as a way to make sense of the world. We see complex things built from simpler things. We recognize similarities of shape and form between different things and judge some more closely related than others. We group individuals and find generalities or abstractions to derive new types or categories. Our intuition tells us that some of these groupings make better sense than others, which causes us to wonder about whether our groupings are artifices or reflect some underlying reality or truth. As we extend these → classifications to more things with more diversity, we can see levels or gradations in how the characters by which we categorize these things diverge. Such step-changes inform what we now call hierarchies. We readily recognize hierarchies and have a commonsense view of what they are. Still, we lack consensus on a formal definition of hierarchy across disciplines. We see great disparities in how to construct hierarchies and what relations between things they represent. Our understanding of hierarchies is imprecise.
While the etymology of the word hierarchy discussed in Section 2 begins with notions of religious and social rank and power, our focus here will be on knowledge systems. As used herein, knowledge systems are the subset of → knowledge organization systems (Hjørland 2016) that may be logically represented to and manipulated by computers, such as taxonomies, classification systems, → thesauri, or → ontologies, as well as knowledge representation languages. This focus is not to deny the importance of the concept of hierarchy in social and political contexts. But these are not central to the role of knowledge systems, and also reflect initial groundings of the term often inconsistent with the sense of hierarchy applied to knowledge and information. Nonetheless, “the way we do classification is not only a reflection of our mainstream culture, it is a tool of that culture, both reflecting and reinforcing it” (Olson 1999, 65). Various perspectives on what hierarchies are in a knowledge system context and how we construct them are reviewed in Section 3.
The thematic importance of classification and hierarchical structure in knowledge systems can best be illustrated using a consistent perspective. Many thinkers could provide such consistency. I have chosen to use the great 19th Century American logician, scientist and polymath, → Charles Sanders Peirce, as our guide. He was perhaps the most coherent thinker on knowledge representation to have lived and very relevant to the representation issues of today (Bergman 2018). Section 4 specifically refers to his theories of signs, logic, pragmatism, and universal categories as we weave this narrative.
These discussions set the basis for a proposed typology of hierarchies in knowledge systems in Section 5. This typology is grounded in the logical methods that Peirce articulated in how to distinguish and separate items using prescission as well as the extensional breadth and intensional depth of information (Peirce 1998b). We argue a ‘natural’ classification reflects an appropriate balance of both parts. Peirce shows how we can define the real without redress to psychologism, how continuity can co-exist with classification, and how we have ways to determine subsumption relations that are real and independent of subjectivity.
The article concludes in Section 6. While we can and should strive for ‘natural’ hierarchies in knowledge systems, so long as our subsumption relations are logical, we can still conduct meaningful inferences across our knowledge system hierarchies, whether real or artificial. How we classify and the logical and consistent use of subsumption relations are the keys to coherent hierarchies in knowledge systems.
2. Etymology and history
Hierarchies — real and artificial — abound throughout nature and human affairs. Some believe everything in the universe is of a hierarchical nature (Annila and Kuismanen 2009; Kulish 2002). A hierarchy places items into a general order. The context of this ordering may vary widely, but the items in this order gradate from the more specific to the more general. In linguistics, this ordering is from hyponym to hypernym [1]. Computer scientist John F. Sowa (2001) has defined a hierarchy as “a partial ordering of entities according to some relation”. In set notation, the more general level subsumes the more specific level.
Hierarchies thus express subsumption relations. To subsume is to “include, absorb, incorporate” (Oxford English Dictionary, sense 6c). The subsumption relation, also called the inclusion relation, means that one item, say A, is more general (or subsumes) its paired item, say B. Hierarchies may, for example, take the form of:
- classification systems [2],
- dendrograms,
- genealogies,
- graphs,
- Hasse diagrams (a mathematical diagram for partially ordered sets),
- ladders,
- levels,
- taxonomies,
- trees.
These uses suggest the hierarchy term also has many possible synonyms [3] and antonyms [4]. Hierarchies are the logical undergirding of inference and reasoning in knowledge systems. Hierarchies, used in classifications, bring organization to our world. Some may view hierarchies in some social contexts as inequitable or oppressive; in other contexts as ranks of skill or accomplishment or power or authority [5]. In our knowledge system context, hierarchies are logical orderings of generality.
Most scholars place the foundations of the concept and etymology of hierarchy with the ancient Greeks. The etymology of the word hierarchy comes from the Greek, ἱεραρχία (hierarchia, or “rule of a high priest”), composed of the roots ἱερεύς (hiereus, or “priest, sacrificer, diviner”) and ἀρχή (arche, or “beginning, origin” and other broad meanings) (Liddell and Scott 1897; Van Hove 1910). Parmenides (ca 475 BC) paired the root concept of hierarchies, the ‘is-a’ relation, with the ‘is-not’ relation, thereby introducing exclusive categories to logic and the idea that a concept may be defined by what it is not (Olson 1999). Plato (ca 360 BC) put forward a method of dividing a general kind into two (dichotomous classification), continuing through further divisions, until finding the exact kind of the thing at hand. Aristotle (ca 300 BC), his student, adopted this approach, however, limiting its application in an important way, as explicated by Parry and Hacker on Aristotelian division and classification logic (1991, 137):
As a process of knowledge, division is characteristically an a priori process based on meaning. Classification, however, is primarily inductive, and may require empirical knowledge. [Often, however, division is considered a kind of classification, see Hjørland 2017]. In a less technical language, this means that a table of pure division can be constructed solely from the meanings of the terms in the table; no recourse to experience is necessary. I know, for example, that squares are a subclass of parallelograms, not from experience, but from the meanings of the terms “square” and “parallelogram”. On the other hand, if I were engaged in the process of classifying plants, I would have to observe the similarities and dissimilarities of actual plants. I could not construct a useful classification of plants unless I had observed the plants I wish to classify.
In the natural sciences, classification is far more important than division, since the principal analyses and relationships are based on empirical data.
Concerning Aristotle’s classification of animals see Pellegrin (1986).
Aristotle’s scala naturae continues to profoundly affect thinking about nature and classification. In about 300 AD Porphyry expressed Aristotle’s categories in dichotomous divisions. This enabled illustration of the categories as a tree structure, a visual form that has an old and rich history (Gontier 2011; Lima 2014) and remains a common metaphor. We often refer to knowledge domains or taxonomic splits as branches, the top-level node shown as a trunk the root, with the (most specific) terminal items in the structure called leaves. (The ‘tree of life’ metaphor known, for example, from Darwin’s Origin of Species (1859), has a different meaning in → genealogical classification, though not all biologists agree it is a model metaphor for development, cf., Mazzocchi 2013 and Quammen 2018.)
Binary classification was termed divisio through Medieval times. The reasons for division were becoming nuanced. Scholars were recognizing part-whole and member-of (instance) relations, and that divisions may be based on either intrinsic (intensional) or external (extensional) means, most notably by the Port Royal logicians as expounded by Hamilton (Peirce 1867). The idea of → logical division arose to capture the top-down process of splitting higher classes into smaller sub-classes in a descending reduction (Frické 2018). These logical methods informed the classification efforts of Linnaeus and many others (an interpretation questioned by some recent historians, cf., Witteveen 2020), and still informs logical division in knowledge organization today (Frické 2018) [6].
Pseudo-Dionysius the Areopagita first used and explained the term hierarchia in his 6th Century works “The Celestial Hierarchy” and “The Ecclesiastical Hierarchy” (Patrides 1974; Van Hove 1910). These works, as also commented upon by St. Maximus of Constantinople and Pachymeres, explained the graded responsibility of ‘hierarchs’ for sacred things. Hierarchs at different grades took actual care of some sacred things, both obeying and commanding, but did not obey those they commanded. A graded celestial hierarchy applied to God at the pinnacle and angels of various orders below; the ecclesiastical hierarchy — that is, humans as a community of believers — was modeled on this structure. “The hierarchy, therefore, connotes the totality of powers established in the Church for the guiding of man to his eternal salvation, but divided into various orders or grades, in which the inferior are subject to and yield obedience to the higher ones” (Van Hove 1910, 1). Over centuries the idea of ‘hierarchy’ was getting more informed though its basis less certain.
These influential works guided the thinking about hierarchy for a millennium (Patrides 1974) [7]. From the 1300s, treatises were published over the next 500 years that extended religious hierarchies into conceptions of the natural order of things. These extensions were a continuation of Aristotle’s ideas regarding elements, grades, and natural classes. Ideas of ‘celestial order’ were adopted and expanded under Aristotle’s notion of scala naturae. The biblical Jacob’s vision of a ladder that extended from heaven to earth (Genesis 28:10-15) sparked the idea of multiple hierarchical ladders throughout medieval times (Patrides 1974). By the early 1800s, this ‘scale of perfection’ was becoming known as the Great Chain of Being (Lovejoy 1971; Mayr 1982; Snyder 2014). By the dawn of scientific awakening, the cosmos and the religious order had become organized around the same hierarchical principles.
“Thus it clearly appears that in Europe at the end of the 17th Century the usage of the word hierarchy had shifted from a limited theological register to other registers outside the field of theology, at the same time undergoing certain alterations” (Verdier 2006, 15). Verdier’s historical treatment of ‘hierarchy’ is strong across the 14th to 19th Centuries, with an emphasis on religion and society. Yet, notably after the emergence of encyclopedias in the 1700s in France and Spain, Auguste Comte in the 1830s began to split areas of knowledge into → disciplines, arguing hierarchies as systems and a general manner of apprehending the organization of knowledge (Verdier 2006).
The attempt to equate the organization of religion with social order and nature was bound to surface inconsistencies where they exist. The Reformation was also undercutting the tight religious hierarchy advocated by the Catholic Church. The extension of a religious hierarchy to all of nature meant that any contradiction found in nature would erode that bond. The schism came to a head in the 1800s, foreshadowed by philosophers such as Leibniz and scientific discoveries like those of Copernicus and Galileo, which removed the Earth from the center of the universe.
An important hierarchical knowledge innovation was Linnaeus’ binomial nomenclature and classification system for organisms, Systema Naturae, in 1735 [8]. The ensuing period was one of innovation and ferment for knowledge systems. Roget published the first hierarchical classification of words into a thesaurus in 1852. Darwin published the Origin of Species in 1859, devoting an entire chapter to classification [9], with his theory of evolution sundering the faultlines over divinity that had been cracking for hundreds of years (Mayr 1982). Though the great chain was breaking in the 1800s, the importance of hierarchy to natural classification and science was only being enhanced. There was truth in some hierarchies, but not in others. In freeing classification from the divine, interest in hierarchies in knowledge and information was able to return to many of its Greek foundations. Dmitri Mendeleev grouped and organized the chemical elements by atomic number into the periodic table in 1869. Melvil Dewey innovated a modern hierarchical library classification system in 1876 [10]; the Library of Congress classification (1897) and Universal Decimal Classification (1904) followed [11].
The term level has been examined in many of philosopher Mario Bunge’s works. Bunge (1960, 404) defined levels as “grades of being ordered, not in arbitrary ways, but in one or more evolutionary series” (see Bunge 1969 for a longer, formal definition and discussion). Joseph Needham (1937) popularized the phrase → integrative levels in a lecture honoring the philosopher Herbert Spencer, based at least in part on the earlier 18th and 19th Century classifications of science by Comte and Spencer (Kleineberg 2017) [12]. The objective was to discern a hierarchical structure of levels from molecules to cells to organizations and, ultimately, societies, ecological systems, and the cosmos. The way to determine hierarchical levels should be more synthetic, less reductionist, and recognize they may be more emergent and complex than their predecessors (Kleineberg 2017). This approach has also been expressed as ‘levels of organization’ (Brooks 2015) and many other kinds of levels (Yao 2009, Table 1). However, there remains no consensus as to what constitutes an integrative level, how it is defined, nor how to sequence or model it (Kleineberg 2017).
3. Perspectives on knowledge hierarchies
Knowledge, like information, is inherently open world and multi-level; it requires a logic that can accommodate the truth that much information is unknown to the community, and current information is fallible (Bergman 2018). Seemingly every knowledge discipline has its own examples or forms of hierarchy [13]. Hierarchies may occur at all levels in knowledge systems within and between classes, instances, and attributes. Hierarchies are the organizing framework for some of the most important knowledge structures. Classification systems and controlled vocabularies are principal structures within, among other fields, libraries and the information sciences. Taxonomies and typologies are common classification structures for natural, physical, and artifactual realms, as well as for words and language morphology. These multi-level hierarchies often express a tree-like structure. Dendrograms are tree-like representations which are mostly based on matrices of correlation coefficients. Biologists Mayr, Linsley and Usinger (1953, iii) defined a dendrogram as a “diagrammatic illustration of degree of relationship based on degree of similarity (morphological and otherwise)”. Many of these approaches, plus more interconnected versions that take on the form of ontologies or graphs, provide the hierarchical backbones to knowledge representation (KR) systems that support inference and logical reasoning (Bergman 2018).
It is not surprising, then, that the diversity of definitions and historical changes in use raise epistemological questions among those who research knowledge hierarchies and classification. “Has the world one unique structure (‘taxonomic monism’), or is there more than one structural entity and process (‘taxonomic pluralism’)? Are the structures of the world mind-independent (realism), or are they artefacts projected into the world (idealism)? Can our classifications be natural, or are they always artificial? These are core issues in the metaphysics of classification” (Hjørland 2017, 110). In the remainder of this section, we explore these questions from theoretical aspects to the nature of the hierarchical expression and the subsumption relation.
3.1 Theories of hierarchy
Many different classifications of ‘hierarchies’ exist. One prominent dimension is whether hierarchies are artificial or real with classification based on ‘natural kinds’ (Bird and Tobin 2018; Peirce 1998b; Brakel 1998), discussed below. Some allow ‘natural classification’ in science, but not in concepts or theoretical objects (Wilkins and Ebach 2014). Another dimension is whether hierarchies are constructed or result from a ‘top-down’ or ‘bottom-up’ manner (Czégel and Palla 2016; Ellis 2004; Lane 2006; Salthe 2012; Walker 2014; Yao 2009). Some believe distinct boundaries are necessary to distinguish things (Durkheim and Mauss 2009), but information theory may help clarify previously blurred distinctions (Ellis 2004; Wu 2013). Some discuss hierarchies of purpose (Herrmann-Pillath and Salthe 2011), another topic to which we will return. Some include concepts such as ‘flow hierarchies’ (Luo et al. 2009), but these are sequential, and not subsumptive.
Pumain recognized specific hierarchical objects and methods in different disciplines but also asked common or transversal questions (2006, 7). She posed three hypotheses for why hierarchical organizations are so frequent in the natural or social systems that we observe, which are not necessarily mutually exclusive:
- Hierarchies are just our way of perceiving and understanding our environment.
- Hierarchies are spontaneous attractors in unconstrained dynamic random processes.
- Hierarchies represent the best solution for many optimization problems.
The first may be termed the idealist/constructivist view on hierarchies; the second the realist perspective; and the third a pragmatic realist perspective. Hjørland poses a refinement with four hierarchical methods: (1) empirical properties; (2) logical principles; (3) historical consensus; or (4) pragmatic purpose (2017). (Ahl and Allen 1996 described a related epistemological issue between definitional versus empirical entities and defended an antirealist position.) What I argue in the remainder of this article is that ‘natural’ hierarchies contain most of these elements. We begin by idealizing what we observe in the real world, but then refine these nascent observed relations into natural ones by testing their intrinsic and extrinsic qualities. We try to adhere to terminology based on ‘scientific’ consensus, broadly and pragmatically construed.
A ‘natural’ classification is grounded in the ‘real’, something that exists independent of what a mind might conceive. However, if we consider the development of, say, biological classifications, it is obvious that many different hierarchies have their adherents (see e.g., Bruce 2003 about the history of classifying birds). Geologist Francis Bather (1927, 71) observed, “not a single naturalist had a clear idea of what he meant by ‘natural’. All he knew was that the other fellow’s classification was unnatural”.
For centuries, a view has been that there is no ‘real’ independent of the mind, a proposition first expounded by Descartes (Mayr 1982; Tobin 2010). Another criticism is observers classify phenomena using their own interpretations, which may distort the underlying truth (Durkheim and Mauss 2009; Hjørland 2018). A pragmatic view reliant on intuition, the scientific method, and the interpretation of signs holds that — while truth is fallible yet still correcting — knowledge of the real can be obtained sufficient to act and to classify (Peirce 1877). Practically, Brakel (1998) suggested Peirce supported pluralist interpretations of natural kinds since, in Peirce’s words, “we cannot be quite sure that the community ever will settle down to an unalterable conclusion upon any given question” (CP 2.655, 1878) [14].
Under a logical classification system, we can see a thing like a car participating in a hierarchy of vehicle products in one context or mechanical devices or prized possessions in others. Even in a bloodline genealogy, each child has two parents. There is nothing inherent to a knowledge hierarchy that limits the number of parents or branches under which an item is subsumed so long as the relationship is real, and the connections are logical. However, for a classification to be ‘natural’ in addition to logical, it should be updated to reflect new consensus knowledge as it arises and should be based on the complete breadth and depth of available information. Classifications and their scope and determination cannot exist independently of their purpose or interpretant. Labels alone are unable to convey how or why we classify things, some more ‘natural’ than others. Section 4 expands further on these Peircean insights.
If some hierarchies are real and a reflection of nature, what is the force that causes them to arise? The economist and systems theorist Herbert Simon (1962) tackled this question in a seminal article, “The Architecture of Complexity”. His argument was that hierarchy arose from complexity in a system of interrelated subsystems, and he defined hierarchy in this way (1962, 468; italics in original):
By a hierarchical system, or hierarchy, I mean a system that is composed of interrelated subsystems, each of the latter being, in turn, hierarchic in structure until we reach some lowest level of elementary subsystem. In most systems in nature, it is somewhat arbitrary as to where we leave off the partitioning, and what subsystems we take as elementary.
In Simon's view (1962, 477), “hierarchies have the property of near decomposability. Intracomponent linkages are generally stronger than intercomponent linkages. This fact has the effect of separating the high-frequency dynamics of a hierarchy — involving the internal structure of the components — from the low-frequency dynamics — involving interaction among components”. His argument used a now-famous analogy of two watchmakers, both interrupted by customers. One watchmaker made his watches with individual and separate parts, the other with a series of pre-assembled modules. When interrupted by customers, the watchmakers would need to return to their last completed step. The watchmaker with independent parts needed to return to the beginning; the other needed only return to the previous sub-assembly. Simon saw this resulting greater productivity and faster assembly as the driving force for hierarchies, similar to how emergent structures may arise in evolution or how problems are solved. “The fact then that many complex systems have a nearly decomposable, hierarchic structure is a major facilitating factor enabling us to understand, describe, and even ‘see’ such systems and their parts” (Simon 1962, 477). “How complex or simple a structure is depends critically upon the way in which we describe it. Most of the complex structures found in the world are enormously redundant, and we can use this redundancy to simplify their description. But to use it, to achieve the simplification, we must find the right representation” (Simon 1962, 481).
This marriage of ‘near-decomposability’ and description became the cornerstone of a field known as hierarchy theory (Ahl and Allen 1996). The theory is a general one that simplifies complexity using this common property of complex systems — near decomposability (Wu 2013). Besides the economist Simon, other roots of the field arose from the chemist, Ilya Prigogine, and the psychologist, Jean Piaget (Allen 2001). One view within the field, held by Simon and most scientific adherents, is that descriptions of hierarchy are a faithful capturing of the true, underlying structure in nature. At the other extreme, description and, thus, understanding of the process are limited by the contexts of the observers (Pattee 1973a) [15]. Pattee (1973b, 75-76) also saw a distinction between structural and control hierarchies, the latter implying an “active authority of the upper level over the elements of the lower levels”, reminiscent of the earliest senses of hierarchy, but without the divinity.
Ecologists and biologists, while recognizing and accommodating hierarchies, also began to appreciate the interconnectedness of nature and its underlying structure in networks (Allen 2001). In particular, Salthe (2012), who initially focused on hierarchy theory, proposed splitting hierarchies into subsumptive and compositional branches, and looked for mechanisms of what causes hierarchy in natural forces as explained by information theory (Salthe 2002; 2009; 2011). Many hierarchies are natural and thus an expression of the real (Annila and Kuismanen 2009). The graph and network metaphors have become prevalent in much thinking about hierarchies. Complexity and hierarchy emerge from the evolution of the entity and its connected network (Corominas-Murtra et al. 2013) or directed acyclic graph (Harmer and Oshurko 2020).
These efforts have not gone without criticism. We have already noted the lack of consensus on scope and definitions for hierarchy. Simon’s approach to complexity has been criticized as ignoring interactions of evolutionary significance (Wimsatt 1972) or proposing a “mysterious” form of it (Lane 2006). What constitutes a ‘level’ is ambiguous with conflicting definitions based on perspective (Eronen 2015). The proxy of complexity might focus too much on material composition in the biological and ecological arena, perhaps better replaced with ideas of scale (Potochnik and McGill 2012).
Anderson (1972) tackled the questions of scale and reductionism in the hierarchy of science in his influential “More is Different” paper in Science. Like Simon, Anderson saw complexity as central to hierarchy (Lane 2006). Anderson endorsed the reductionist hypothesis, generally accepted by scientists, that animate and inanimate matter are controlled by the same set of fundamental laws (Anderson 1972). But he saw the reverse, which he termed a ‘constructionist hypothesis’, as breaking down when faced with scale or complexity. “Instead, at each level of complexity entirely new properties appear, and the understanding of the new behaviors requires research which I think is as fundamental in its nature as any other” (Anderson 1972, 393). He speculated that at growing scale the symmetry of the collection must break because of the tension between two inherent properties, determinism and randomness. These broken symmetries lead to hierarchies, specialized functions, or both. Broken symmetries lead to the emergence of new forms of symmetry with new laws and properties. The ‘rigid’ information of the new level is contained in regular spatial or temporal structures such as crystals, DNA, or language. The emergent level need not have all of the laws that govern its constituents and generally has fewer (Lane 2006). Models of various interactions based on simple rules were shown to produce hierarchical organization — one of the “landmarks” of ‘emergence’ — wherein complexity, new properties, and new functions may arise from simple elements (Holland 1998).
Rather than complexity, Patrides’ (1974) learned historical view of hierarchy was to equate the concept with the idea of ‘order.’ Kauffman (1993) much expanded the theme of order into concepts related to self-organization and evolution (1993). Within computer science, a new era of interest in hierarchies was also emerging driven by general-purpose languages and artificial intelligence. Doyle provided one of the first investigations of how to capture hierarchy within a knowledge representation language (Doyle 1977). Hierarchies, and the algorithms to represent them, were understood as keys to representing logic, to learning, and to reasoning over knowledge bases. Abductive inferences promised the ability to generate and test hypotheses. Decidability — that is, the ability for computer evaluation programs to run to completion — became a criterion for efficiency and language design. Generalized subsumption and description logics emerged as a strong model (Buntine 1988). How to treat part-of (mereological) relations in a hierarchical manner was added to the mix (Padgham and Lambrix 1994). Description logics, which are the basis for current leading semantic technology languages such as RDF or OWL, generalized the use of hierarchies through subsumption, and are now a central part of knowledge representation languages (Baader et al. 2003; Brachman and Levesque 2004; McGuinness and Borgida 1995; Napoli 1995).
3.2 Hierarchical objects and relations
Though rarely stated, everything having to do with hierarchies is informational. A hierarchy is an expression of a relation — superordinate or subordinate — that is an assertion, so thus information, between two paired objects, A and B. By convention, A is at a higher (more general) level in the hierarchy; that is, closer to the root. In a genealogical context, A is the parent and B is the child. Either A or B may be one of the following kinds:
- generals - which may be known as classes, sets or types;
- instances - which may be known as individuals, particulars, or members;
- parts of - which may be standalone parts in assemblages or differentiated integral parts, and may also be (reciprocally) known as containers; or
- properties - relations which have a subsumptive character.
However, of course, depending on the relation specified, not all kinds of A may be associated with any kind of B or vice versa. The subsumption relationship stated for the relation needs to assert the proper super- or subordination [16].
Further, not all A ↔ B relations have a hierarchical nature. Associations, label or name assignments, descriptions, and non-directional actions are all non-hierarchical relations [17]. An entry within a hierarchy is connected to items at next adjacent levels in the hierarchy by one or more relations [18]. Hierarchical relations may be internal or external in outlook, a major division as we will soon see. The particular nature of the hierarchical relation may be unstated in some cases, but those found in knowledge systems are often explicit to improve inferencing power.
One method, widely employed since the students of Socrates, is to recognize the differentia within intensional attributes to distinguish a genus from a species, with the prototypical example being ‘man is a rational animal’ (Burek 2004). An intensional definition is one that has a delimiting characteristic (Roche 2016), in this case the essential differentiator of rationality. Linnaeus applied this method in his plant and animal classifications, but has been criticized for proposing an artificial system, despite the provisional nature of his phylogenies, criticisms further compounded by confusing uses of the intensional and extensional terms (Vasilyeva and Stephenson 2008). As another example, extensional definitions are often and confusedly treated differently in information science and mathematical sets (Roche 2016). Further, some systems change the meaning of classification methods depending on context (Quinn 2017). We also see conflicting terms for when we are trying to compose intensional or extensional definitions as opposed to specifying the logical relation (Kublikowski 2016).
To help clarify these matters, let’s first look at an extensional hierarchical relation, one which is external in outlook. The extensions of an object are those things to which it applies. The relationship of an instance or member to a set or class of other instances that share (mostly) the same characteristics is an extensional one. Denotation is a synonym. A hierarchical relation based on extension is the enumeration of instances with these shared same characteristics. To illustrate this, let’s look at how we might classify the concept of ‘color’ by assembling up all of the colors we can name, like emptying all of the individual sticks from a crayon box:
This ‘color’ class is logical as it is built from an enumeration of its group members, that is the sticks contained in our crayon box. Group instances of an extensional hierarchy share many descriptive characters. Bigger boxes of crayons lead to the enumeration of more colors (or sticks) for these instances with their shared attributes. For example, peach ‘is-a’ color. (It is also a fruit, which reinforces the need to not use simple labels and to disambiguate them for knowledge systems.) All instances of the crayon sticks share the broader ‘color’ concept, and as crayon sticks, share sibling characteristics that qualify them as instances. Extensional subsumptions are more common between classes or classes and members but are not limited to them.
Still, there is an ‘essence’ to color, to use Aristotle’s criteria for natural classes, that we can argue is based on something inherent to color, intrinsic to it, what makes up its essential character. It is what the Port Royal logicians called comprehension, later re-labeled intension (Peirce 1867) [19]. In the case of our ‘color’ example, one essence we can surmise is the idea of primary colors, more-or-less centroids of the colors we can see [20], keyed to our visual cones, as arrayed in Figure 2.
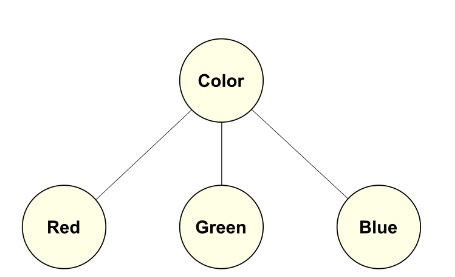
We now have a ‘color’ class constructed from an essential character or attribute, which is a primary color. This diagram is an example of intensional subsumption. Attributes are inherent, internal, integral, or intrinsic to the thing at hand.
A well-chosen intensional schema may bring additional advantages. In the case of the intensional ‘color’, the essential differing character of primary color gives us the power to combine attributes into blends, which give us a multiple-level hierarchy with some secondary colors as well.
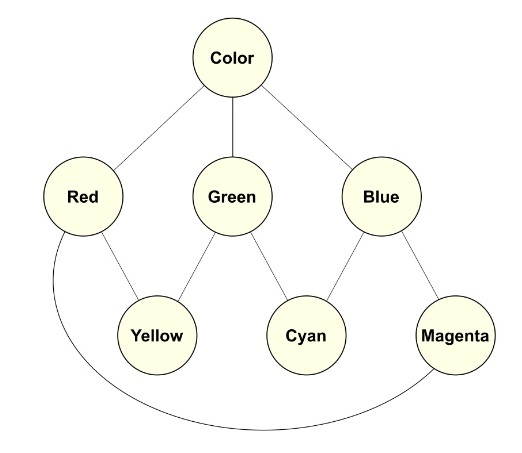
Though the essence of primary colors arose from Newton’s determination in 1665 that color was an inherent character of the visible light spectrum (Gleick 2004), it was not until about 1800 that Herschel and Ritter discovered infrared and ultraviolet wavelengths, respectively (Newman 2013). By the end of the 1800s, intensional colors as seen by humans were understood as the wavelengths of electromagnetic radiation between the infrared and ultraviolet, with a blend of secondary colors. Today, however, we know that both bees and birds can see in the ultraviolet, while humans can not, and we can see red, while other mammals can not. We might now revise our understanding of intensional color for all animals to be the wavelengths of the electromagnetic spectrum between the infrared and far-ultraviolet. New knowledge or changes in extensional scope may change our understanding of a what is a ‘natural’ class.
We can take any two bubbles in the figures above and their connecting link and present them as a ‘triple’ subject-predicate-object statement — that is, a basic assertion — in the World Wide Web Consortium (W3C) vocabularies (2008). The key logical statements made in a KR language assert these subsumptive relationships [21]. In this manner we can see a small, direct portion of the immediate hierarchies, only now turned from a section of a vertical tree into a horizontal ‘triple’ statement.
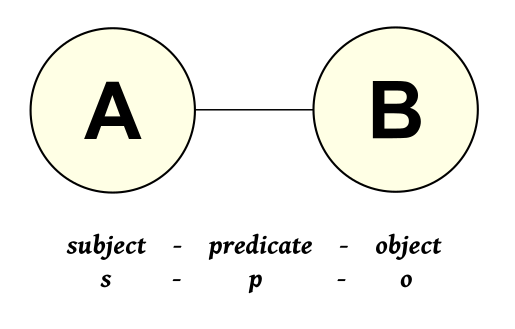
This tuple approach is a fairly universal form, reflective, for example, of entity-relationship or entity-attribute-value (EAV) data models (Chen 1976), in addition to those from the W3C and description logics. In this manner, we can include hierarchical statements in broader assemblages of other assertions in our knowledge systems.
3.3 Subsumption in knowledge representation
Library and information scientists perhaps view knowledge systems through the initial lens of thesauri or classification. Knowledge representation (KR) occupies the most developed end of the scale of knowledge systems since the objective is to instruct computers in how to capture and coherently model knowledge. Doyle (1977, 3), in the first comprehensive study of KR languages, noted: “Hierarchy is an important concept. It allows economy of description, economy of storage and manipulation of descriptions, economy of recognition, efficient planning strategies, and modularity in design”.
Perhaps the best description of hierarchies in a KR context is from description logics (DL) (Baader et al. 2003). The subsumption relation is the basic inference or reasoning relation in DL (Baader et al. 2003; Guarino and Welty 2002). In part, DL grew out of Peirce’s early work in predicate logic (Brink, Britz and Schmidt 1994). DL is the logical basis for the semantic languages such as RDF or OWL standardized by the W3C (2008); they have an open-world logical premise well-suited to knowledge [22]. KR systems can certainly classify, often with useful automation, but their greater power arises from their ability to conduct reasoning and inference, chiefly due to their hierarchical subsumption relations, the essential backbone to KR systems (Burek 2004; Doyle 1977).
We create a chain of inheritance when we connect hierarchical levels to adjacent ones using the same subsumption relation (or predicate) using an s-p-o statement such as in Figure 4 wherein the object of a first assertion is the subject of a second (or vice versa). For example, the logical consequence, or entailment, of asserting that a person is a mammal, which is an animal, and which is a living thing thus enables us to deductively reason that a person is a living thing. A deductively sound argument is where we base the conclusion on truthful premises. On the other hand, we could ask if a given living thing is a person or not. Inductively, we can trace the hierarchy back from living thing to person to determine if it is possible for a person to be a living thing, but our inductive power would be weak because there are many potential kinds of living things. To strengthen the argument, we would need to improve the likelihood by adding more lines of evidence, such as the living thing under consideration walks bipedally, is dimorphic, is of a certain size, bears live young, nurses them with milk, is hairy, and manipulates symbols.
Sometimes the is-a relation is equated with the subsumption relation, but it is only an important subset; all of the relations we discuss in our later typology are subsumptive in nature. The common is-a relation masks at least four different sub-types of subsumption [23] subject to different logical inferences and entailments (Johansson 2006). Brachman (1983) made a logical analysis of is-a and its types in the beginning years of description logics. We can further subset partitive subsumptions using the part-of and has-part relations.
The work we can extract from KR systems with hierarchical subsumption relations extends beyond reasoning and inferencing. For example, much can be done with basic text. Hearst (1992) demonstrated that lexico-syntactic patterns could indicate hyponym relationships. Heuristics were used to identify these initial patterns and has remained a useful approach. At roughly the same time, however, particularly through the understanding of hierarchical structures in text, an alternate approach was to treat the semantics of a terminology in algebraic form (Brink and Schmidt 1992). These computational approaches have continued to be refined, initially to inform cluster analysis (Cimiano and Staab 2005). In the last decade, word embeddings, which convert natural language text into vectors of numeric representations, have shown the ability to distinguish semantic similarities and differences through vector comparison. The growing sophistication of word embeddings led about five years ago to their use in the discovery of hypernym-hyponym relations (Fu et al. 2014). The present state of development has moved beyond text snippets and documents associated with specific nodes to embrace the entire graph structure, with subsumption relations playing a prominent role. The intersection of text, hierarchy, graph structure, and adjacency features is leading to an explosion of graph embedding approaches that promise to improve on virtually all KR tasks (Hogan et al. 2020).
In other work areas, we can check instances using subsumption, though we may need to add some further steps (Donini et al. 1994). We may leverage hierarchies to inform different clustering algorithms, including for formal concept analysis (Cimiano and Staab 2005). When building our knowledge structures, we can test for ‘satisfiability’, which means that our assertions are ‘true’ and consistent with other assertions, a key qualification criterion. Subsumptive relations are the basis for these tests (Horrocks and Patel-Schneider 1999). The subsumption hierarchies are also useful structures for aligning our knowledge systems, which we need to do when merging or adding large chunks to them (Spiliopoulos, Vouros and Karkaletsis 2010). Hierarchies can inform the automatic creation of metadata facets (Stoica and Hearst 2004; Stoica, Hearst and Richardson 2007). Given these interactions, we can also apply hierarchical clustering to our existing structures, which can surface natural data representations that may be better ways to arrange (and thus refine) our knowledge structures going forward (Greenberg et al. 2020). Subsumption relations also add meaningful features over which machine learners can inductively reason for creating more effective artificial intelligence (AI) models.
High-quality subsumption relations confirm that broader and narrower relations are stronger than those among sibling concepts, that superclasses exhibit commonalities among their sub-classes, and that there are abstract features in a superclass not exhibited by any sub-class (Solskinnsbakk et al. 2010). Crutchfield (2012) used Shannon’s (1948) information theory to further explicate the emergence of natural hierarchies. His analysis showed how a ‘higher’ level may emerge from the properties of a ‘lower’ level. Note how those findings relate to Anderson’s (1972) earlier Science paper. The proliferation of ‘triples’ throughout a KR system also leads to the formation of a network or graph structure, significantly aided by the presence of a hierarchical organization (Czégel and Palla 2016). Graph structures themselves are sources of additional features for machine learners, and leverage the potential to extract meaningful information from the natural language contained within the knowledge structure.
The use of ‘hierarchy’ in the sciences and, now, also knowledge professions, has thus both narrowed and shifted from its historical senses over time [24]. The narrowing occurs by focusing on subsumption relations for natural observations and conceptual generalizations. The shift occurs to computable logic tests and algorithms. Hierarchies, in the sense of knowledge systems, are now the reasoning basis for understanding the real world, as opposed to expressions of control or social rank [25]. Yet, as these broad surveys have shown, considerable diversity exists as to the nature and classification of knowledge hierarchies.
4. Insights from Peirce
Charles Sanders Peirce (1839–1914, pronounced ‘purse’) belongs to the pantheon of great thinkers in knowledge representation (Bergman 2018). Peirce made significant contributions in logic, mathematics, the physical sciences, scientific notations, philosophy, dictionary definitions, and many practical fields over a nearly sixty-year period, including thirty years as a practicing scientist and inventor (Burch 2017). While widely recognized and feted as a younger man, he died penniless and somewhat in obscurity; 80,000 handwritten manuscript pages are still awaiting editorial attention to join his more than 12,000 published ones (Burch 2017). Among his signal contributions are the philosophy of pragmatism (different from, but a stimulant to, the similar advocacies of his friends and colleagues, William James and John Dewey), his semeiotic theory of signs (different than the linguistic efforts of Ferdinand de Saussure), the algebraic logic of relatives, algebraic geometry and topology, explications of the scientific method, diagrammatic logic using existential graphs [26], and a third method of logical inference, abduction [27]. In a more contemporary vein, Peirce has contributed a triadic logic to formal concept analysis (Wille 1995) [28], presaged key aspects of category theory (Zalamea 2012), and has stimulated practical applications in hypothesis testing, grammars, cluster analysis, artificial intelligence, and other areas of computer science (Burch 2017), including description logics as noted earlier.
Peirce’s background as a classifier derives from his reliance on the universal categories of Firstness, Secondness, and Thirdness; his understanding of everything being represented as signs, subject to interpretation, fallibility, and community understanding; his fierce (and idealistic) belief in reality; and his logics. Infused in these perspectives is his embrace of the scientific method, indeed even extended to his notion of pragmatism, wherein we find guidance as to what practical questions to ask and how to act under uncertainty. I expand on each of these areas in the sub-sections to follow.
There are also strong linkages in Peirce’s insights to evolution and Shannon’s information theory (Bergman 2018). His simultaneous beliefs in non-deterministic chance (which he termed ‘tychism’) and continuity and generality (which he termed ‘synechism’) bracket the actual, all three of which he viewed as real. While the idea of ‘hierarchy’ in knowledge systems will likely remain imprecise, the use of a consistent perspective such as what Peirce provides can give us a coherent approach for representing information of all forms and levels to our knowledge systems.
4.1. Peirce, the classifier
Peirce was a classifier and a keen student of classification. At Harvard, Peirce studied under the renowned taxonomist Louis Agassiz, and greatly admired his natural classification system and used animal lineages in many of his examples (Bergman 2018). Peirce largely adhered to Plato’s Socrates in arguing for ‘natural classes’, whose ideal for dividing classes was “where the natural joints are, and not trying to break any part” (Plato 1925). Peirce also embraced Aristotle’s idea of a ‘final cause’ of a thing, which he likened to the purpose or the reason for the thing’s existence, over Aristotle’s ‘essence’ (Hulswit 1997). Peirce referred to a natural class as a “family whose members are the sole offspring and vehicles of one idea, from which they derive their peculiar faculty” (Peirce 1998b, 125). His recognized means for natural classification was “only an enumeration of tests by which the class may be recognized in any one of its members” (CP 1.223, 1902). Peirce’s concept of ‘natural classes’ was not limited to things only found in nature but included social classes, the sciences, concepts, ideas, thoughts, and human-made products (Bergman 2018; Brakel 1998; Hulswit 1997). Peirce denied that a ‘final cause’ was static, meaning the referent was not unchangeable, and he was attentive to remove the psychological from classification, grounding it instead in logic and observed phenomena.
Peirce’s most notable classification was that of the sciences (Midtgarden 2019), which he broadly defined to include philosophy, logic and the humanities [29]. He worked on this system for nearly 40 years until he produced his final ‘perennial’ one in 1903, having iterated and refined his classification at least 20 different times with minor versions in between (Kent 1987). The perennial classification had the three main branches of mathematics, cenoscopy (philosophy), and idioscopy (the special sciences of traditional science and the humanities). The classification is hierarchical in design. Another major classification by Peirce was on ‘Logic’ as reflected in his Carnegie grant application of 1905 and related papers (Peirce 1998e), though a myriad of classifications is common across his five decades of writings. He applied the tree metaphor in classification and logic (Anellis and Abeles 2016; Peirce 1976).
To Peirce, any logical inquiry needed to be grounded in a ‘speculative grammar’ that defines the qualities, objects and rules resident to the domain. In one of Peirce’s first papers, read before the AAAS, he presented his views on comprehension (intension) and extension, which he labeled depth and breadth respectively (Peirce 1867). In this paper Peirce examined the logical underpinnings of these concepts reaching back to the Greeks, the scholastics of the Middle Ages, the Port Royal logicians, and more recent philosophers and logicians, noting many confusions and inexactitudes. Peirce maintained that depth and breadth multiplied together consists of the total information, or area, of the concept or object, positions which he continued to hold for at least the next 40 years (Peirce 1998b). He assigned degrees to this possible information, including what is essential and what is substantial (absolute truth). Peirce likened comprehension (intension), or depth, to ‘internal qualities’ (Kant), forms (DeMorgan), particulars, or connotations. Depth consists of the necessary internal attributes common to the item. On the other hand, extension, or breadth, is an external quality (Kant) or scope (DeMorgan), that denotes something and is applicable to generals and universals. In extension, all group members are brought in relation to one another via their shared characteristics (Peirce 1867). In a classificatory structure, what is most general has the greatest breadth and little depth; what is individual and particular has the greatest depth and little breadth.
Peirce therefore presents a logical means for assigning subsumption relationships. Classifications are more natural when they distinguish items by virtue of their essential internal qualities, and when they are combined into classes with a common ‘final cause’. The final cause goes beyond essentiality to capture the ‘purpose’ or directionality for the item at hand as reflected by its continuous evolutionary tendencies to certain forms of generality. This viewpoint is sometimes confused with the teleology of Aristotle, but instead reflects a more subtle and rational aspect of natural science; it is a “type for which selection is made” (Short 2007, 138).
A natural classification for Peirce is thus logical and both intensional and extensional. (We can still have logical classifications that are artificial.) It is intensional when particulars are properly distinguished based on essential, internal characters. It is extensional when we bring those particulars together in an appropriate scope based on their ‘final cause’ as exemplified by their evolutionary directionality or purpose. Further, given the fallibility of knowledge, a natural classification is provisional and subject to change and refinement as new knowledge arises [30].
4.2. Trichotomies in logic, signs, and reality
Most researchers of Peirce soon see his penchant for threes (Bergman 2018; Burch 2017). The fount for Peirce’s insights seems to reside in his abiding interest in logics and relations, going back to his earliest writings. His ‘reduction thesis’, much studied by Burch (1991), maintained that all n-ary relations beyond an n of three may be constructed from triadic relations alone, and no true triadic relation (‘Mike gives the ball to Jim’) may be constructed by monadic or dyadic relations. A number of parties has now claimed proof of Peirce’s reduction thesis (Burch 1991; Dau and Correia 2006; Hereth and Pöschel 2011). My reading of Peirce suggests he used triadic approaches in his own thinking to question prevalent dichotomous arguments and to be explicit about the use of logic, analysis and synthesis when tackling a new problem. We certainly see evidence of this in Peirce’s systems thinking regarding logic, signs and reality, or any “intellectual concept” to use his term (Peirce 1998d). This kind of triadic thinking can also aid classification and hierarchies in knowledge systems.
From his earliest papers, Peirce challenged the then-current notion of only two forms of inferential logic, namely deduction for necessary inferences and induction for probable ones (Burch 2017). He explicated these two forms much during his career, for example identifying classification as the first of three stages of induction (Peirce 1998g), but also felt there was a third kind of logic, employed when generating hypotheses and deciding how to select among them, what he initially called ‘abduction’ (later ‘retroduction’, then ‘abduction’ again) [27]. Peirce worked much on abduction given its role in the complete logic of the scientific method, and he refined his view of it over his career. The growth of new knowledge, and the stimulus for classification, comes from a “surprising fact” that causes us to question premises or understand new emerging or discovered phenomena, which compels abductive reasoning to pick a candidate hypothesis for why the “surprise” has occurred. Multiple factors weigh on that choice among an infinitude, including economy, practicality, probability, and even instinct. Then, “that which is to be done with the hypothesis is to trace out its consequences by deduction, to compare them with results of experiment by induction, and to discard the hypothesis [if refuted], and try another” (Peirce 1998c, 107).
The three inferential forms of abduction, deduction and induction constitute the ‘critic’, the actual methods of logical inference, which along with ‘speculative grammar’ (noted above) and ‘methodeutic’, comprise Peirce’s broader triadic logic. Methodeutic (which Peirce also called ‘speculative rhetoric’) deals with all methods of representation, inquiry, and verification, and is closely aligned with the apparatus and thinking of science (Burch 2017); it is what also led Peirce into the study of signs. Peirce held the triadic system of logic to be universally true (Zalamea 2013).
Peirce equated logic in its broadest (triadic) sense with his theories of semeiosis of sign-making and interpretation (Burch 2017), distinct from the more linguistic interpretation of ‘semiosis’ (de Saussure) with which it is often conflated. The trichotomy of the sign consists of the immediate object (2ns), its signal (1ns), and its interpretation (3ns). The immediate object is a facsimile of the full, dynamic object, since how it can be signaled and represented can never be complete. The signal can extend from an icon or index or pointer to the object to a symbol of it (such as a word). The interpretation of the sign is based on the context and capabilities of the interpretant. According to Peirce, the interpretant is that to which the sign represents the object, which he often called mind or ‘effete mind’, which we perhaps can more generally understand as the receiver of the information. Signs build upon signs through a process of accretion and community consensus, often from the coining and acceptance of new terms based on the understanding of new emergent properties or aspects of the object. Science and the application of logic enable us to continually add to our language and to test and refine these understandings.
Peirce organized these various classifications, as with most other aspects of his work, into a trichotomy of universal categories, most often referred to as Firstness, Secondness, and Thirdness. Peirce articulated more than 60 different variants of these categories over his career, from logic to signs to language symbols and other classifications, varying the actual content of each category depending on the context (Bergman 2018, Table 6-2, 118-120). The universal categories are the primitives that comprise all things, ideas, logic, and concepts, since nothing is as irreducible as one, two, and three, with all higher-order structures combinations of these constructs. The groundings for the categories are: Firstness (1ns) - monads which are the possibilities for a given context; Secondness (2ns) - the actual things within that context, specifically including events and entities; and Thirdness (3ns) - the generalities, laws, or abstractions that provide continuity across things (Bergman 2018). For example, a mode of signs from possible to actual to necessary was termed by Peirce ‘mark’ (1ns), ‘token’ (2ns), and ‘type’ (3ns) (CP 8.364, 1908). Similarly, we can relate Shannon’s (1948) information model of sender (2ns), message (1ns), and receiver (3ns) to Peirce’s triadic categories.
Peirce came to believe that all three universal categories — possibilities, actualities, and generalities — are real, becoming what Fisch (1967) called a ‘three-category realist’. The actual things of the world (2ns) exist independent of what we think of them. Peirce saw generalities (3ns) and ‘natural classes’ as real because general principles (such as the law of gravity) are operative in nature, they are essentially predicative, and their representations (such as words) can have real effects (Peirce 1998h) [31]. Firstness was the last universal category that Peirce accepted as real in about 1897 (Fisch 1967). Peirce based his assertion, in part, on the “perceptual judgment of qualities” (1ns) that are “utterly beyond control” of the interpretant (Peirce 1998d, 191). That is, “perceptual judgments [which he elsewhere calls ‘Qualities of Feeling’] are the first premisses of all of our reasonings and that they can not be called into question” (Peirce 1998d, 191). Thus, in two fundamental ways — a trichotomous vs. dichotomous basis and a complete belief in an external reality — Peirce contradicted Descartes’ view of the world.
4.3. Fallibility, the scientific method, and pragmatism
As a practical physical scientist, Peirce understood well that knowledge and science are fallible, and measurements are not perfectly reproducible, no matter the scale or how many taken. Historical and emerging notions of natural order are not inviolate. For example, we see the scientific understanding of the taxonomic ordering of living things has progressed from the use of morphology and external appearances to internal ones based on genealogy and, now, genetics (Mayr 1982). The role of evolution in these orderings has been fundamental, such that some observers suggest that “various evolutionary processes naturally emerge with hierarchical organization” (Annila and Kuismanen 2009). Peirce’s insights triangulate a central role for evolution consistent with semeiosis and the 2nd law of thermodynamics (Annila and Kuismanen 2009; Annila and Salthe 2010; Herrmann-Pillath 2010; Herrmann-Pillath and Salthe 2011; Lehmonen and Annila 2017; Salthe 2012; Short 2007).
Peirce saw absolute truth as something that can only be approached as a limit function. The aim of science is to employ keen observation, logic, and sound methods to strive toward those limits. Peirce’s insight with pragmatism was to provide a scope, and practical and economic ways to gain the necessary knowledge sufficient for us to be able to act and make progress (Peirce 1905a; 1905b; 1906; 1998d; 1998e). Of all four methods of inquiry, only knowledge gained through the scientific method provides the means for us to fix belief sufficient to act (Peirce 1877).
The integration of the three logical tests of abduction, deduction, and induction into what he called the “scientific method” is one of Peirce’s signal achievements (Burch 2017). The methodology is error-correcting (Mayo 2005) and acknowledges that “probability is actually a notion with clear empirical content and that there are clear empirical procedures for ascertaining that content” (Burch 2017). The nature of knowledge and truth as limit functions means there should be no absolutes in intellectual discourse. If a system or approach, including one of classification, is in the main truthful and respectful of the scientific method, then whole systems should not be rejected based on a minority of falsities; instead, the errors should be corrected and the system revised. Given the broad scope that Peirce ascribed to knowledge and the sciences, these guidances apply to all disciplines, including philosophy and the humanities, as well as questions of practical conduct. Mathematics was the sole branch of knowledge he held apart.
We can and do reach consensus or belief on many aspects of how the world is and how it works, sufficient for us to ‘know’ things to act upon them. Peirce embedded this belief in his philosophy of pragmatism (Parker 1998). The act of classification or the placement into hierarchies is, of course, not always a natural one. Peirce recognized that “there are artificial classifications in profusion, but [there is] only one natural classification” (CP 1.275, 1902). Peirce makes the practical point that, “All classification, whether artificial or natural, is the arrangement of objects according to ideas. A natural classification is the arrangement of them according to those ideas from which their existence results” (CP 1.231, 1902). And, further, “All natural classification is then essentially, we may almost say, an attempt to find out the true genesis of the objects classified. But by genesis must be understood, not the efficient action which produces the whole by producing the parts, but the final action which produces the parts because they are needed to make the whole. Genesis is production from ideas. […] A science is defined by its problem; and its problem is clearly formulated on the basis of abstracter science” (CP 1.227, 1902).
Peirce’s worldview is one where logic and the application of the scientific method intersects with a Nature that is continuously evolving in particular contexts within chance and the limits of its possibilities. What we know about this Nature is incomplete and fallible. How we perceive and communicate these realities are imperfect. The depth and breadth of our information space are constantly changing, and so should our systems of classification within it. The wonderful thing about picking Peirce as our guide is the remarkable coherence and completeness his ‘architectonic’ (Peirce 1891) brings.
5. A typology of knowledge system hierarchies
The foregoing points to the importance of logic and the striving for ‘natural’ classes within both intensional and extensional viewpoints in formulating our hierarchical knowledge systems. This section proposes a typology of knowledge system hierarchies based on these points and guided by Peirce. Our proposed typology for hierarchical relations should in all cases be logical, and then strive for naturalness within a subsumptive framework. However, to bootstrap this process, we first need to introduce a logical relation called prescission that was employed by Peirce and is hierarchical, but does not have most of the entailments of subsumption.
Every hierarchical statement can be seen as a pair of objects connected by a super- or suborienting relation (as reflected in Figure 4). In accordance with his universal categories, Peirce defines three distinct kinds of separation for any pair in thought; that is, ways in which we assign conceptual or intellectual relations between a pair. As paraphrased, dissociation (1ns) consists in imagining one of the two separands without the other, complete or incomplete. Prescission (2ns) consists in supposing a state of things in which one element is present without the other, the one being logically possible without the other. Discrimination (3ns) consists in representing one of the two separands without representing the other (EP 2:270, 1903). Note that all hierarchical subsumptions are 2ns; that is, prescissive in nature. Prescission captures the most fundamental expression of a hierarchical relationship, stated as the relation, prescind [32]. We can understand the relation ‘B prescinds A’ as equivalent to ‘B may be supposed without A’; the more common form is ‘B can be prescinded from A’. Other ways to understand the relation is that B may ignore, be presupposed without, or can be considered separately from, A. It is a logical process absent any psychologism to distinguish a subordinate concept from a superordinate one (CP 2.248, 1903):
But prescission, if accurately analyzed, will be found not to be an affair of attention. We cannot prescind, but can only distinguish, color from figure. But we can prescind the geometrical figure from color; and the operation consists in imagining it to be so illuminated that its hue cannot be made out (which we easily can imagine, by an exaggeration of the familiar experience of the indistinctness of hues in the dusk of twilight). In general, prescission is always accomplished by imagining ourselves in situations in which certain elements of fact cannot be ascertained. This is a different and more complicated operation than merely attending to one element and neglecting the rest.
Prescission is an asymmetrical separation of two elements objectively considered; it is a logical operation that does not make any ontological assumptions about the two elements (Houser 2010). Prescission carries no connotation of meaning. It can determine logical precedence between two concepts, and therefore a level, but not an exact relation between them. It carries no entailment other than prescission [33]. Though Peirce does not state such, in all cases a particular can be prescinded from a general. However, Peirce does state that Firstness prescinds Secondness, which prescinds Thirdness, though none of the reciprocals hold true (Peirce 1998e). This means that prescission is the most general relation for establishing a hierarchy, useful for abstract concepts or monads. For these reasons, we put precission at the top of our typology hierarchy.
The next major level in the hierarchy is subsumption. All subsequent hierarchical relations are sub-types underneath the rubric of the subsumption relation. The subsumption relation may involve classes, instances, parts or properties, and may be extensional, intensional (comprehensive), or ‘natural’ embracing both (Peirce 1867; Vasilyeva and Stephenson 2008), consistent with the breadth and depth terms employed by Peirce. The most restrictive subsumption level in the typology is the ‘natural’ one. Again, consistent with Peirce, a ‘natural’ subsumption has both a defined (defensible) scope for its parent class (its breadth, or extension), and a set of essential intrinsic attributes for its object (its depth, or intension).
Table 1 now weaves these threads into a typology for hierarchy relations useful to knowledge systems. Consistent with our guidance from Peirce and our desire to maintain inheritance across subtypes of subsumption, we agree with Linnebo and Rayo (2012) who argue that hierarchies should be expressed through types that exhibit characteristics of absolute generality and inferencing [34]. I have organized the remainder of the typology by subsumption relations, split into its major extensional, intensional, and ‘natural’ branches. I further organize each of these splits to embrace the common hierarchical relations drawn from: (1) the American National Standards Institute as developed by the National information Standards Organization (ANSI/NISO 2005); (2) semantic language standards for knowledge systems from the World Wide Web Consortium (W3C 2008); and (3) other researchers with interests in typing hierarchical relations.
Table 1: Typology of hierarchical types (The sources used are provided as table notes)
Type of Hierarchy
Illustrative Relation
Notes Prescission B prescinds A 1
B can be supposed without A 1
B is logically possible without A 1
Subsumption A is more general B
A subsumes B
A includes B
A broader than B 3
A broader term B 4
B narrower than A 3
B narrower term A 4
B nests within A 2
Extensional Subsumption B is a A 2,5,6
is-a [class] B subClassOf A 3
A superClassOf B 7
A broader term (generic) B 4
B narrower term (generic) A 4
determinable-subsumption B subPropertyOf A 3,8
specialization B is specialization of A 8
is-a [instance] B type A 3
A has member B 7
B instance of A
A broader term (instance) B 4
B narrower term (instance) A 4
A has an instance of B 7
Intensional Subsumption
6,9
A contains B 2
is-a [class] As above
genus-subsumption A is parent of B 8
B is child of A
specification B is way of A 8
B is method for A
part-of A has part B 2,6,7
A broader term (partitive) B 4
B narrower term (partitive) A 4
B is region of A
B is time slice of A
has-a A has attribute B
A [property] B 3,10
defeasible A usually has attribute B 11
‘Natural’ Subsumption See text
Table Notes: Synonym relations are italicized; reciprocal relations are underlined in relation to first given instance; 1: see text; 2: (“Hierarchy” 2020); 3: W3C predicate (W3C 2008); 4: (ANSI/NISO 2005); 5: Tbox in DL; ‘levels of organization’ (Ahl and Allen 1996); 6; ’compositional hierarchy’ and ‘specification hierarchy’ are extensional and intensional, respectively (Salthe 2012); 7: (ISO 2011); 8: (Johansson 2006); 9: Abox in DL; ‘levels of observation’ (Ahl and Allen 1996); 10: in W3C sense, individually specified properties (W3C 2008); 11: (Britz and Varzinczak 2017).
Each classification, as indicated by an entry under ‘Type of Hierarchy’ in Table 1, may be illustrated by one or more relational expressions (predicates). The first entry for each classification is the standard or common one; synonym relations are italicized and reciprocal relations are underlined if there are multiple illustrations. A and B are the paired hierarchy objects for each illustrated relation; by convention, A is taken to be the more general object closer to the root of the tree. More general and abstract hierarchical relations tend toward the top of the table, more particular toward the bottom. Realize there are many nuances to these examples within actual deployments [35]. Note as one progresses deeper into the hierarchy that the relations become more constrained and the entailments fewer. The most general A-B assertions with the broadest entailments occur at the higher (top) levels of the hierarchy. Also, note there can be difficulties assuming equivalence of terms between different classification systems; refer to the cited sources for nuances.
All of these relations, if used consistently, may each be assembled into a logical hierarchical chain across multiple levels. That chain may be tested for consistency and, if it is, may be used to trace inheritance or make inferences up and down the chain. Beyond this logical construction, the aim is to strive for ‘natural’ subsumptions. The tests that get applied are the same abductive, deductive, and inductive ones defined by Peirce, embedded in his broader logic triad including properly scoped grammar and methods. A ‘natural’ hierarchical placement is one where the scope of the extension captures the purpose or ‘final cause’ of the class and where instances are qualified based on shared, essential characters. A ‘natural’ hierarchy is one where the placements are natural, and the structure reflects greater generality at the top and greater depth at the bottom. A ‘natural’ knowledge hierarchy is aspirational since its inputs are fallible, and warrants updates as new knowledge arises.
We can contrast the typology in Table 1 to other classifications. For example, the English Wikipedia entry on ‘hierarchy’ lists four types of hierarchy: nested; containment; subsumptive containment; and compositional containment (“Hierarchy 2020”). The nested example is like Russian matryoshka dolls where each doll neatly fits within a larger one [36]. The last two types are themselves subtypes of containment, which is subsumed under subsumption. The Wikipedia classification is not widely used and appears to be a mostly semantic variant. Another proposed but unused classification is from the earlier cited hierarchy book, wherein Pumain posited three types of hierarchical meaning: (1) order and subordination; (2) taxonomy; or (3) ordered set of elements (Pumain 2006).
One widely used scheme is the generic, whole-part and instance relationships common to library classification hierarchies (Zeng 2005) (see also the Appendix). This classification has continued through ISO standards in 2011 (ISO 25964-1: 2011) and 2017 (ISO 5127: 2017). A family of schemes are widely used in biology based on the genus subsumption, though with varying bases for evidence and internal or external viewpoints. In spirit the closest to our proposed typology — at least from the standpoints of embracing notions of natural classification, information and reality — is the model hierarchical system proposed by Cottam et al. (Cottam, Ranson and Vounckx 2016), somewhat informed by Peirce. They recognize similar concepts and drivers to what we propose. However, they unduly rely upon the concept of scale, do not relate their approach to the historical use and understanding of hierarchies, and therefore introduce terminology and aggregations too foreign to legacy understandings. In contrast, the typology proposed in Table 1 can be seen as a synthesis across the disciplines of information science, computer science, and knowledge representation, generally faithful to historical terminology and concepts, and consistent with the logic of C.S. Peirce.
6. Conclusion
This article has covered many historical and epistemological aspects of the concept of hierarchy, which remains imprecise. We have seen there are multiple relations covered by the concept of hierarchy, with is-a, part-of, has-a, and member-of being prominent ones. We have seen, over more than two thousand years, that the logic applied to hierarchies has come to recognize scientific facts and this diversity of relations. We have the sense that some (perhaps the exemplary) hierarchies are natural and based in reality. There is something real and cognizable with the pattern of hierarchies, but we are still seeking explanatory mechanisms.
To somewhat deal with this imprecision, we have narrowed our view to hierarchy in knowledge systems, which has the advantage of a tractable and understandable scope of theories and approaches. We have used the insights of the 19th Century logician and philosopher, Charles Sanders Peirce, to help guide our inquiries. Peirce’s commitment to realism is itself an expression of his idealism. His commitment to logic includes separation in thought (Peirce 1998a) — that is, dissociation, prescission, and discrimination — which is a handy aid to evaluating the knowledge landscape and the process of categorization (which we barely explored herein), and a logical triad of signs, inference methods, and methodologies that we did explore directly related to hierarchical classifications. Peirce anticipated much in our current discourse, so much so that he would likely have appreciated today’s topical areas like computers, ontologies and knowledge graphs (Burch 2017).
This background has enabled us to create a typology of hierarchical relations for knowledge systems. We have suggested a logical way to organize hierarchical relations that are varied and have different entailments, so that we need to choose which to apply in a given context carefully. Our first order of business with this typology is a logical hierarchy so that we can do inference and reasoning. That consideration has included description logics, themselves outgrowths from Peirce’s logic, as the core formalism for capturing subsumption relations in hierarchies with an open world viewpoint consistent with the nature of knowledge. The knowledge system languages and vocabularies from the W3C are grounded in these logics.
Peirce’s guidance has emphasized that truth is fallible, and continued application of the scientific method is the best way to keep our assignments current and relevant. We should expect our typology of ‘hierarchy’ to evolve. Further, there are ways to strengthen knowledge systems and their subsumption relations to improve reasoning and inference power. For example, we can distinguish different kinds of subsumption relations more akin to the types shown in Table 1. Or, we can classify and better distinguish different kinds of things subject to those relations. The split between relations and things is one example, as are classing things into different populations such as ‘parts’ and ‘wholes’ and being consistent in how we treat those sub-classes. Depending on the KR language used, we may have other options [37].
But logic is only the starting point, the essential foundation to hierarchical classification. We need to embrace the Peircean viewpoint that natural hierarchies are real, and should be the extensional purpose of our inquiry, what Peirce likened to a ‘final cause’. We investigated a realistic combination of driving factors, consistent with these viewpoints, that can explain both the rationale and modes of unfolding of natural hierarchies. Evolution is central to these viewpoints, which acts contextually and is constrained by history and chance.
We have matched Peirce’s views on the meaning of information with Claude Shannon’s theories on the entropy and communication of information messages (Kraskov et al. 2005). In local situations where the influx of external energy is great — such as exists on biotic Earth due to solar radiation — favored hierarchical structures are those through chance recombinations that maximize entropy production from free energy (Annila and Kuismanen 2009; Annila and Salthe 2010; Salthe 2012). The glue that mediates this interplay of information and structure, on the one hand, with energy gradients, on the other, is evolution. Random variations in varying contexts create the favored functions or structures that maximize the energy flux. It is not unreasonable to associate the drivers of natural hierarchies in reality (including chance) (1ns), information (2ns) and evolution (3ns), as consistent with Peirce’s universal categories and his general theories of logic and semeiosis.
One way to test this thesis is further critical inquiry into the concepts and methods involved, the Firstness of the speculative grammar and the Thirdness of the methodeutic in Peirce’s triadic logic. We also need to probe further the idea of abductive reasoning, part of the Secondness of that triad. One ensuing prediction is that abductive reasoning will support a better understanding of ‘final cause’ via pragmatic ways to screen attribute and evolutionary context. We should also be able to compile and critically evaluate embedded information for components using methods like pairwise mutual information or information entropy at various levels of natural hierarchies, similar to what Chaisson (2001) has demonstrated for energy rate densities. Since our objective in this article has been knowledge systems, we should also be able to develop computer programs and algorithms that explicitly express these Peircean concepts. Working and testable systems are the next logical step.
How we construct our hierarchies, this article has argued, should be subject to tests of logic, science, and coherence. Hierarchical classifications do not have magic breakpoints between generals and particulars. Rather, there is a gradation as fine-grained as the depth in the hierarchy and as wide as the broadest level, just as Peirce asserted. Change is natural, which means revision of hierarchies should be as well. Untended knowledge hierarchies are as unwanted as false assertions.
Acknowledgments
I would like to thank an anonymous reviewer for supporting comments. I would especially like to thank the editor for detailed review, hard questions, and suggestions for additional useful citations.
Endnotes
1. WordNet 3.1 defines: “hyponym, subordinate, subordinate word (a word that is more specific than a given word)” and “hyponymy, subordination (the semantic relation of being subordinate or belonging to a lower rank or class)” opposed to “hypernymy, superordination (the semantic relation of being superordinate or belonging to a higher rank or class)”. ‘Hyponymy’and ‘hypernymy’are inverse to one another. A specific item in one of these relationships is a ‘hyponym’ or ‘hypernym’, respectively.
2. This list is not exhaustive and many of the terms have overlapping meanings (for example, dendrograms are kinds of trees, and taxonomies are often considered synonyms for classification systems, cf., Hjørland 2017, §3.4). Each of these terms — and others not listed — appears in italics in the text where it is first used and defined. The exception is Hasse diagrams, defined in the listing. The historical use of some of these terms in biology is presented by Archibald (2014). Wilson (1969), after discussing various definitions, distnguishes three kinds of hierarchy in nature: (1) physical (fundamental particles, molecules, crystals and cosmic aggregates); (2) biological (from virus structures to the human nervous system); (3) geometrical; and five kinds of hierarchy in artifact: (1) software (such as codes, languages, programs and search strategies); (2) hardware (including computers, transportation systems and cities); (3) organizations (e.g., files, management schemes and social systems); (4) cognition (e.g., levels of knowing); (5) epistemology, which cites works on the classification of knowledge and disciplines.
3. Depending on context (see text), possible noun synonyms for hierarchy include absorption, abstraction, categorization, classification, composition, containment, echelon, embodiment, embracement, generalization, gradation, grouping, inclusion, ladder, level, minor premise, nest, order, partial order, pecking order, rank, scale, schema, stratification, subset, subsumption, subtype, superordination/subordination, taxonomy, or vertical.
4. Depending on context (see text), possible antonyms for hierarchy include absence, anarchy, disorder, equal, equivalent, exclusion, flat, same, unclassifiable, unordered, unranked, and other negations of synonyms.
5. Material in this article was heavily drawn from (Bergman 2018); the author thanks the publisher, Springer, for allowing use of this material.
6. Note the clade-oriented International Code of Phylogenetic Nomenclature (PhyloCode) (cf., Benton 2000; Sluys, Martens and Schram 2004) allows a rank-free representation in addition to the rank-based classification known from Linnaeus (e.g., displaying the following ranks: domain, kingdom, phylum, class, order, family, genus, and species).
7. Patrides provides an impressive survey of history up through the Renaissance. Unfortunately, he too easily equates order as synonymous with hierarchy, which does have an important overlap in the mathematical sense, but which diminishes somewhat the power of the arguments strictly related to hierarchy.
8. I am excluding the largely alphabetical organization systems of the first library catalog (ca 275 BC), English library catalog (ca 800 AD), dictionaries (1604), or encyclopedias (1728) (Bergman 2016).
9. Chapter 13 in the first edition of On the Origin of Species (p. 411-458) is devoted to classification, including morphology and embryology (Darwin 1859).
10. The first hierarchical library classification is reported for China sometime before AD 1 (Miksa 1994); by ‘modern’ we agree with Miksa the 19th Century classifiers provided broader and deeper subcategories geared to knowledge.
11. This expansion of the scope of knowledge systems continued when Claude Shannon published his information theory in 1948, and the structure of DNA was elucidated in 1953. The first computer database dates from 1962 (Bergman 2016).
12. Kleineberg (2017) provides a historical treatment much richer than here, a useful compilation of ‘levels’ from various authors, and more than 200 references.
13. A diversity of examples in alphabetic order include animal behavior (Paine and Tani 2005), astronomical objects (Shapley 1958), chemical compounds (Simon 1962), classification of the sciences (Peirce 1998a), controlled vocabularies (ANSI/NISO 2005), dendrograms (tree diagrams) (Kraskov et al. 2005), design methodologies (Alexander 1964), Earth processes (Kleidon 2010), ecological systems (Allen 2001), electrocardiograms (Kraskov et al. 2005), emergence of life (Walker 2014; Walker and Davies 2013), fractals (Cottam, Ranson and Vounckx 2013), genetic inheritance (Simon 1962), hadronic collision jets (particle physics) (Cacciari, Salam and Soyez 2008), human needs (Maslow 1954), human social organization (Simon 1962), industry sectors (Luo et al. 2009), living organisms (phylogenetic trees) (Kraskov et al. 2005; Simon 1962), natural languages (Chomsky 1956), physical-material-biological-sociocultural levels (Salthe 2009), primitive social classifications (Durkheim and Mauss 2009), subtypes of cancer (Sørlie et al. 2001), taxonomies of concepts (Cimiano and Staab 2005; Di Beneditto and de Barros 2004), and word relationships (G. A. Miller 1995). Donna Wilson (1968) also provided a much longer (but older) listing of examples in a bibliography to a hierarchical structure symposium.
14. We base the general method for citing direct Peirce quotes on his Collected Papers (Peirce 1931) followed by volume, page, and year (e.g., “CP 1.425, 1903”), except as otherwise cited.
15. Again, we see this tension for the role of observers in the assessment of the reality of hierarchies, a topic Peirce informs through his theory of signs, or semeiosis, discussed in Section 4.
16. Though it is possible to express a sequential order via the specific preceeds time relation to obtain a so-called ‘flow’ hierarchy applicable to events or processes (Luo et al. 2009), this is a special edge case that we exclude from further consideration.
17. See further Peirce’s classification of signs, “Nomenclature and Divisions of the Triadic Relations, as Far as They Are Determined” (Peirce 1998f), and Section 4.
18. As part of a decade-long effort to improve best practices in subject referencing (D. Miller, Olson and Layne 2005), the American Library Association assembled a listing of nearly 30 hierarchical pairs based on Michel (1997) that recognized class-instance, whole-part, compositional, anatomical, topical, and other relationships.
19. Peirce preferred the term comprehension and disliked the term intension, believing it too easily confused with ‘intensity’ (Peirce 1867). Nonetheless, we use intension herein because of its accepted usage.
20. J.W. von Goethe (1749-1832) first proposed the standard 3-color scheme. Today, most designers use a 4-color scheme from Ewald Hering (1834-1918).
21. Some knowledge representation languages allow n-ary relationships. Some knowledge representation languages may also allow specification for how a property behaves, including symmetry, transitivity, reflexivity, commutativity, or cardinality. The is-a relation, for example, is commonly understood to be both transitive and reflexive (Nilsson 2006). See further Zadeh’s paper on similarity relations (Zadeh 1971).
22. Description logics data models are easier to expand and update than conventional transaction data systems because they follow an ‘open world’ formal logic assumption (Bergman 2009). The open-world assumption (OWA) conforms to Peirce’s views of knowledge and truth. We can add missing values without altering the data schema. OWA is limited to inferences and deductions from what is known to be true (or deemed likely true), in keeping with the open-ended nature of knowledge. “OWA is useful when we represent knowledge within a system as we discover it, and where we cannot guarantee that we have discovered or will discover complete information” (Bergman 2018a, 161).
23. These four kinds of ‘is-a’ relationship are genus-subsumption, determinable-subsumption, specification, and specialization (Johansson 2006); see Table 1 in text.
24. Again, recognizing the split with social and political perspectives on the concept of hierarchy.
25. A fourth major dictionary sense emerged in the 1800s that defined ‘hierarchy’ as “A body of persons or things ranked in grades, orders, or classes, one above another; spec. in Natural Science and Logic, a system or series of terms of successive rank (as classes, orders, genera, species, etc.), used in classification” (Oxford English Dictionary, sense 4).
26. In logic, besides his insights and proving of theorems, Peirce invented and developed dozens of logical operators, syntax, and diagrammatic systems for expressing and proving logic concepts (Burch 2017).
27. Peirce specifically rejected abduction in favor of retroduction in 1898 believing the initial translation of Aristotle to be in error (Peirce 1992b), but had returned to using abduction by the time of his 1903 Harvard Lectures on Pragmatism (Peirce 1997). Abduction remains the more commonly used.
28. Rudolf Wille, the initial formulator of formal concept analysis, extended this logic to embrace the trichotomies of Charles Peirce (Wille 1995). In formal concept analysis, a rigorous mathematical approach, formal concepts consist of two parts: an extent, which is a subset of objects to which it belongs; and, an intent, which is a subset of attributes shared by sibling concepts (Stumme 1999). These notions correspond exactly to the idea of extensional and intensional subsumptions as used herein.
29. Peirce’s conception (and definition) of science was close to the German term Wissenschaft (Burch 2017).
30. The provisional nature of knowledge and science is a constant theme throughout Peirce’s writings.
31. According to Peirce, continuity “is shown by the logic of relatives to be nothing but a higher type of that which we know as generality. It is relational generality” (Peirce 1992a, 258).
32. Peirce also termed this concept precission, prescisive abstraction, prescision, or precisive abstraction (CP 4.235, 1902). It comes from the same root as precision in measurements but has a different meaning as described in the text, which is one reason we prefer the spelling of prescission to distinguish it as much as possible.
33. However, prescind may also be usefully employed as a logical operator to restrict the relevant population of consideration for a given inquiry.
34. This paper also makes strides in bringing conventional set theory into conformance with description logics (Linnebo and Rayo 2012).
35. Cottam et al. (2016), who believe hierarchies are basic in knowledge systems, have also proposed a model abstraction over hierarchical relation types, different than the typology presented in Table 1. Their approach is also based on Peirce’s universal categories but also adds Ivan Havels’ ‘three levels of reality’.
36. In Peirce’s existential graphs, nesting is a very important operator that is best left to a separate discussion (Zalamea 2003).
37. For some KR languages such as either RDFS (the schema extension to RDF) or OWL, we can sub-class properties, meaning we can boost the inferencing power of our predicates. We can add domain or range restrictions to our properties that establish the subjects or objects, respectively, to which the predicate may apply. For OWL, we can further specify the logical behavior we want our relations to exhibit, such as transitivity or reflexivity, or we can take advantage of its ‘punning’, which enables us to metamodel a class as also being an instance depending on its context, helpful when we want to treat a class as an instance unto itself. We may also use extension or intension to assign instances to classes, or may create hierarchies of properties through the subPropertyOf predicate.
References
Ahl, Valerie, and Timothy F. Allen. 1996. Hierarchy Theory: A Vision, Vocabulary, and Epistemology. New York, NY: Columbia University Press.
Alexander, Christopher. 1964. Vol 5, Notes on the Synthesis of Form. Harvard University Press.
Allen, Timothy F. 2001. “A Summary of the Principles of Hierarchy Theory”. International Society for the Systems Sciences. https://web.archive.org/web/20011218001638/http://isss.org/hierarchy.htm (March 4, 2020).
Anderson, Philip W. 1972. “More Is Different: Broken Symmetry and Nature of Hierarchical Structure of Science”. Science 177, no. 4047: 393–96.
Anellis, Irving H., and Francine F. Abeles. 2016. “The Historical Sources of Tree Graphs and the Tree Method in the Work of Peirce and Gentzen”. In Modern Logic 1850-1950, East and West: Studies in Universal Logic, eds. Francine F. Abeles and Mark E. Fuller. Cham: Springer International Publishing, 35–97. http://link.springer.com/10.1007/978-3-319-24756-4_3 (January 12, 2021).
Annila, Arto, and Esa Kuismanen. 2009. “Natural Hierarchy Emerges from Energy Dispersal”. Biosystems 95, no. 3: 227–33.
Annila, Arto, and Stanley Salthe. 2010. “Physical Foundations of Evolutionary Theory”. Journal of Non-Equilibrium Thermodynamics 35, no. 3: 301–21.
ANSI/NISO. 2005. Guidelines for the Construction, Format, and Management of Monolingual Controlled Vocabularies. Baltimore, Maryland: National Information Standards Organization. https://groups.niso.org/apps/group_public/download.php/12591/z39-19-2005r2010.pdf.
Archibald, J. David. 2014. Aristotle's Ladder, Darwin's Tree: The Evolution of Visual Metaphors for Biological Order. New York: Columbia University Press.
Baader, Franz, Diego Calvanese, Deborah L. McGuinness, Danielle Nardi and Peter F. Patel-Schneider (eds.). 2003. The Description Logic Handbook: Theory, Implementation and Applications. New York, NY: Cambridge University Press.
Bather, Francis Arthur. 1927. "Biological Classification: Past and Future". An Address to the Geological Society of London at Its Anniversary Meeting on the Eighteenth of February 1927. Quarterly Journal of the Geological Society of London 83, no. 1-5: 62-104.
Benton, Michael J. 2000. “Stems, Nodes, Crown Clades, and Rank-Free Lists: Is Linnaeus Dead?” Biological Reviews 75, no. 4: 633-48. https://doi.org/10.1111/j.1469-185X.2000.tb00055.x.
Bergman, Michael K. 2009. “The Open World Assumption: Elephant in the Room”. AI3: Adaptive Information, Adaptive Innovation, Adaptive Infrastructure (blog). http://www.mkbergman.com/852/the-open-world-assumption-elephant-in-the-room/ (September 18, 2017).
Bergman, Michael K. 2016. “A Timeline of Information History”. AI3: Adaptive Information, Adaptive Innovation, Adaptive Infrastructure (blog). http://www.mkbergman.com/temp-exhibit/ (March 3, 2020).
Bergman, Michael K. 2018. A Knowledge Representation Practionary: Guidelines Based on Charles Sanders Peirce. Cham: Springer International Publishing. http://link.springer.com/10.1007/978-3-319-98092-8 (October 10, 2019).
Bergman, Michael K. 2018a. “KR Vocabulary and Languages”. In A Knowledge Representation Practionary: Guidelines Based on Charles Sanders Peirce, ed. Michael K. Bergman. Cham: Springer International Publishing, 151–80. https://doi.org/10.1007/978-3-319-98092-8_8.
Bird, Alexander, and Emma Tobin. 2018. “Natural Kinds”. In The Stanford Encyclopedia of Philosophy, ed. Edward N. Zalta. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/spr2018/entries/natural-kinds/ (December 30, 2020).
Brachman, Ronald J. 1983. “What Is-a Is and Isn’t: An Analysis of Taxonomic Links in Semantic Networks”. Computer 16, no. 10: 30–36.
Brachman, Ronald J., and Hector J. Levesque. 2004. Knowledge Representation and Reasoning. Morgan Kaufmann. https://www.elsevier.com/books/knowledge-representation-and-reasoning/brachman/978-1-55860-932-7 (October 3, 2017).
Brakel, Jaap van. 1998. “Peirce's Natural Kinds”. In C.S. Peirce: Categories to Constantinople: Proceedings of the International Symposium on Peirce, Leuven, 1997, eds. J. van Brakel and M. van Heerden, Leuven, Belgium: Leuven University Press, 31-45. Preprint available at https://www.researchgate.net/publication/318878227_Peirce’s_natural_kinds.
Brink, Chris, Katarina Britz, and Renate A. Schmidt. 1994. “Peirce Algebras”. Formal Aspects of Computing 6, no. 3: 339–58.
Brink, Chris, and Renate A. Schmidt. 1992. “Subsumption Computed Algebraically”. Computers & Mathematics with Applications 23, no. 2–5: 329–42.
Britz, Katarina, and Ivan José Varzinczak. 2017. “Context-Based Defeasible Subsumption for DSROIQ”. In Proceedings of the Thirteenth International Symposium on Commonsense Reasoning (Commonsense-2017), Nov 6-8, 2017, eds., Andrew S. Gordon, Rob Miller, and György Turán, CEUR Workshop Proceedings, Vol. 2052, London, UK: 1-7.
Brooks, Daniel Stephen. 2015. “The Concept of Levels of Organization in the Biological Sciences”. Ph.D. Bielefeld University. https://pub.uni-bielefeld.de/download/2786539/2786540/DSBrooks_Diss_2014._rev.2015.pdf (March 6, 2020).
Bruce, Murray (2003). “Foreword: A Brief History of Classifying Birds”. In Handbook of the birds of the world Vol. 8, eds. Josep Del Hoyo, Andrew Elliott and David Christie. Barcelona: Lynx Edicions, 11-43.
Bunge, Mario. 1960. “Levels: A Semantic Preliminary”. The Review of Metaphysics 13, no. 3: 396-406.
Bunge, Mario. 1969. “The Metaphysics, Epistemology, and Methodology of Levels”. In Hierarchical Structures: Proceedings of a Symposium, Douglas Advanced Research Laboratories, eds. Lancelot Law Whyte, Albert George Wilson, and Donna M. Wilson. Douglas Advanced Research Laboratories, Huntington Beach, CA: Elsevier Publishing Company, 17–28.
Buntine, Wray. 1988. “Generalized Subsumption and Its Applications to Induction and Redundancy”. Artificial Intelligence 36, no. 2: 149–76.
Burch, Robert. 1991. A Peircean Reduction Thesis: The Foundations of Topological Logic. Lubbock, TX: Texas Tech University Press.
Burch, Robert. 2017. “Charles Sanders Peirce”. In The Stanford Encyclopedia of Philosophy, ed. Edward N. Zalta. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/fall2017/entries/peirce/ (October 23, 2017).
Burek, Patryk. 2004. “Adoption of the Classical Theory of Definition to Ontology Modeling”. In Artificial Intelligence: Methodology, Systems, and Applications, Lecture Notes in Computer Science, eds. Christoph Bussler and Dieter Fensel. Berlin, Heidelberg: Springer Berlin Heidelberg, 1–10. http://link.springer.com/10.1007/978-3-540-30106-6_1 (December 30, 2020).
Cacciari, Matteo, Gavin P. Salam, and Gregory Soyez. 2008. “The Anti-Kt Jet Clustering Algorithm”. Journal of High Energy Physics 2008, no. 4: 63–63.
Chaisson, Eric J. 2001. Cosmic Evolution: The Rise of Complexity in Nature. Cambridge, MA. Harvard University Press.
Chen, Peter Pin-Shan. 1976. “The Entity-Relationship Model — Toward a Unified View of Data”. ACM Transactions on Database Systems (TODS) 1, no. 1: 9–36.
Chomsky, Noam. 1956. “Three Models for the Description of Language”. IRE Transactions on Information Theory 2, no. 3: 113–24.
Cimiano, Philipp, and Steffen Staab. 2005. “Learning Concept Hierarchies from Text with a Guided Agglomerative Clustering Algorithm”. In Proceedings of the ICML 2005 Workshop on Learning and Extending Lexical Ontologies with Machine Learning Methods, Bonn, Germany. ICML, 1–10.
Corominas-Murtra, B., J. Goni, R. V. Sole, and C. Rodriguez-Caso. 2013. “On the Origins of Hierarchy in Complex Networks”. Proceedings of the National Academy of Sciences 110, no. 33: 13316–21.
Cottam, Ron, Willy Ranson, and Roger Vounckx. 2013. “A Framework for Computing Like Nature”. In Computing Nature, Studies in Applied Philosophy, Epistemology and Rational Ethics, eds. Gordana Dodig-Crnkovic and Raffaella Giovagnoli. Berlin, Heidelberg: Springer Berlin Heidelberg, 23–60. http://link.springer.com/10.1007/978-3-642-37225-4_2 (March 13, 2020).
Cottam, Ron, Willy Ranson, and Roger Vounckx. 2016. “Hierarchy and the Nature of Information”. Information 7, no. 1: 1–10.
Crutchfield, James P. 2012. “Between Order and Chaos”. Nature Physics 8, no. 1: 17–24.
Czégel, Dániel, and Gergely Palla. 2016. “Random Walk Hierarchy Measure: What Is More Hierarchical, a Chain, a Tree or a Star?” Scientific Reports 5, no. 1: 17994.
Darwin, Charles. 1859. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: J. Murray. (A facsimile was published 1964 by Harvard University Press.)
Dau, Frithjof, and Joachim Hereth Correia. 2006. “Two Instances of Peirce's Reduction Thesis”. In Proceedings of Formal Concept Analysis: 4th International Conference (ICFCA 2006)Dresden, Germany, February 13-17, 2006, , eds. Rokia Missaoui and Jürg Schmid. LNAI 3874. Springer-Verlag Berlin Heidelberg: 105–18.
Di Beneditto, Marco Eugênio Madeira, and Leliane Nunes de Barros. 2004. “Using Concept Hierarchies in Knowledge Discovery”. In Advances in Artificial Intelligence – SBIA 2004, eds. Ana L. C. Bazzan and Sofiane Labidi. Berlin, Heidelberg: Springer Berlin Heidelberg, 255–65. http://link.springer.com/10.1007/978-3-540-28645-5_26 (February 13, 2020).
Donini, Francesco M., Maurizio Lenzerini, Daniele Nardi, and Andrea Schaerf. 1994. “Deduction in Concept Languages: From Subsumption to Instance Checking”. Journal of Logic and Computation 4, no. 4: 423–52.
Doyle, Jon. 1977. Hierarchy in Knowledge Representations. MIT Artificial Intelligence Laboratory. Working Paper. http://dspace.mit.edu/handle/1721.1/41988 (October 24, 2017).
Durkheim, Emile, and Marcel Mauss. 2009. Primitive Classification. (Routledge Revivals). London: Routledge.
Ellis, George F. R. 2004. “True Complexity and Its Associated Ontology”. In Science and Ultimate Reality, eds. John D. Barrow, Paul C. W. Davies, and Charles L. Harper, Jr. Cambridge University Press, 607–36. https://www.cambridge.org/core/product/identifier/CBO9780511814990A044/type/book_part (February 22, 2020).
Eronen, Markus I. 2015. “Levels of Organization: A Deflationary Account”. Biology & Philosophy 30, no. 1: 39–58.
Fisch, Max. 1967. “Peirce’s Progress From Nominalism Toward Realism:” The Monist 51, no. 2: 159–78.
Frické, Martin. 2018. “Logical Division”. Knowledge Organization 43, no. 7: 539–49. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/logical_division.
Fu, Ruiji et al. 2014. “Learning Semantic Hierarchies Via Word Embeddings”. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Stroudsburg, PA: Association for Computational Linguistics, 1199–1209.
Gleick, James. 2004. Isaac Newton. New York, NY: Vintage.
Gontier, Nathalie. 2011. “Depicting the Tree of Life: The Philosophical and Historical Roots of Evolutionary Tree Diagrams”. Evolution: Education and Outreach 4: 515–38. DOI 10.1007/s12052-011-0355-0.
Greenberg, Craig S., Sebastian Macaluso, Nicholas Monath, Ji-Ah Lee, Patrick Flaherty, Kyle Cranmer, Andrew McGregor and Andrew Mccallum. 2020. “Compact Representation of Uncertainty in Hierarchical Clustering”. arXiv:2002.11661 [physics, stat]: 1–21.
Guarino, Nicola, and Christopher Welty. 2002. “Identity and Subsumption”. In The Semantics of Relationships, Information Science and Knowledge Management, eds. Rebecca Green, Carol A. Bean, and Sung Hyon Myaeng. Dordrecht: Springer Netherlands, 111–26. http://link.springer.com/10.1007/978-94-017-0073-3_7 (March 14, 2020).
Harmer, Russ, and Eugenia Oshurko. 2020. “Knowledge Representation and Update in Hierarchies of Graphs”. arXiv:2002.01766 [cs]: 1–25.
Hearst, Marti A. 1992. “Automatic Acquisition of Hyponyms from Large Text Corpora”. In Proceedings of the 14th Conference on Computational Linguistics, Nantes, France. Association for Computational Linguistics, 539. http://portal.acm.org/citation.cfm?doid=992133.992154 (February 29, 2020).
Hereth, Joachim, and Reinhard Pöschel. 2011. “Peircean Algebraic Logic and Peirce’s Reduction Thesis”. Semiotica 2011, no. 186: 141–67. DOI: https://doi.org/10.1515/semi.2011.050.
Herrmann-Pillath, Carsten. 2010. “Entropy, Function and Evolution: Naturalizing Peircian Semiosis”. Entropy 12, no. 2: 197–242.
Herrmann-Pillath, Carsten, and Stanley N. Salthe. 2011. “Triadic Conceptual Structure of the Maximum Entropy Approach to Evolution”. Biosystems 103, no. 3: 315–30.
“Hierarchy”. 2020. Wikipedia. https://en.wikipedia.org/wiki/Hierarchy.
Hjørland, Birger. 2016. “Knowledge Organization”. Knowledge Organization 43, no. 6: 475-84. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/knowledge_organization.
Hjørland, Birger. 2017. “Classification”. Knowledge Organization 44, no. 2: 97–128. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/classification.
Hjørland, Birger. 2018. “Epistemology of Classification with Emphasis on Emile Durkheim and Marcel Mauss”. In Fondements épistémologiques et théoriques de la science de l’information-documentation. London: ISTE Group, 3.
Hogan, Aidan et al. 2020. “Knowledge Graphs”. arXiv:2003.02320 [cs]: 1–130.
Holland, John H. 1998. Emergence: From Chaos to Order. First Edition. Reading, MA: Perseus.
Horrocks, Ian, and Peter F. Patel-Schneider. 1999. “Optimizing Description Logic Subsumption”. Journal of Logic and Computation 9, no. 3: 267–93.
Houser, Nathan. 2010. “Peirce, Phenomenology, and Semiotics”. In The Routledge Companion to Semiotics, Routledge companions, ed. Paul Cobley. London; New York: Routledge, 89–100.
Hulswit, Menno. 1997. “Peirce’s Teleological Approach to Natural Classes”. Transactions of the Charles S. Peirce Society: 722–72.
ISO 25964-1: 2011 (E). Information and Documentation - Thesauri and Interoperability with Other Vocabularies - Part 1: Thesauri for Information Retrieval. Geneva: International Organization for Standardization.
ISO 5127: 2017(E). Information and Documentation: Foundation and Vocabulary. 2nd edition. Geneva, Switzerland: International Organization for Standardization.
Johansson, Ingvar. 2006. “Four Kinds of Is_A Relations: Genus-Subsumption, Determinable-Subsumption, Specification, and Specialization”. In Contributions to the Third International Workshop on Philosophy and Informatics (WSPI2006), Saarbrücken, Germany, eds. B. Klein, I. Johansson and T. Roth-Berghofer. IFOMIS Reports: 47–62.
Kaufmann, Stuart. 1993. The Origins of Order: Self-Organization and Selection in Evolution. New York: Oxford University Press.
Kent, Beverley E. 1987. Charles S. Peirce: Logic and the Classification of the Sciences. Kingston: McGill-Queen’s University Press.
Kleidon, Axel. 2010. “Life, Hierarchy, and the Thermodynamic Machinery of Planet Earth”. Physics of Life Reviews 7, no. 4: 424–60.
Kleineberg, Michael. 2017. “Integrative Levels”. Knowledge Organization 44, no. 5: 349–79. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/integrative_levels.
Kraskov, Alexander, Harald Stögbauer, Ralph G. Andrzejak, and Peter Grassberger. 2005. “Hierarchical Clustering Using Mutual Information”. EPL (Europhysics Letters) 70, no. 2: 278-84. DOI: https://doi.org/10.1209/epl/i2004-10483-y.
Kublikowski, Robert. 2016. “Definitions and the Growth of Knowledge: The Main Ideas”. Summarium 1, no. 65: 45–57.
Kulish, Victor V. 2002. Hierarchical Methods: Hierarchy and Hierarchical Asymptotic Methods in Electrodynamics. Springer Science & Business Media.
Lane, David. 2006. “Hierarchy, Complexity, Society”. In Hierarchy in Natural and Social Sciences, ed. Denise Pumain. Dordrecht: Springer Netherlands, 81–119. http://link.springer.com/10.1007/1-4020-4127-6_5 (March 1, 2020).
Lehmonen, Lauri, and Arto Annila. 2017. “Natural Classes and Natural Classification” (unpublished manuscript). http://www.helsinki.fi/~aannila/arto/classes.pdf (October 12, 2017).
Liddell, Henry George, and Robert Scott. 1897. A Greek-English Lexicon. New York: American Book Company.
Lima, Manuel. 2014. The Book of Trees: Visualizing Branches of Knowledge. New York: Princeton Architectural Press.
Linnæus, Carolus. 1735. Systema naturae, sive Regna tria naturae, systematice proposita per classes, ordines, genera, & species. Lugduni Batavorum: Apud T. Haak.
Linnebo, O., and A. Rayo. 2012. “Hierarchies Ontological and Ideological”. Mind 121, no. 482: 269–308.
Lovejoy, Arthur O. 1971. The Great Chain of Being: A Study of the History of an Idea. Cambridge, Mass.: Harvard University Press. https://www.hup.harvard.edu/catalog.php?isbn=9780674361539.
Luo, Jianxi, Daniel E Whitney, Carliss Y. Baldwin, and Christopher L. Magee. 2009. “Measuring and Understanding Hierarchy as an Architectural Element in Industry Sectors”. Working Paper 09-144, May 2009, Harvard Business School, Chicago, Illinois: 47 pp. https://www.hbs.edu/ris/Publication%20Files/09-144.pdf.
Maslow, Abraham Harold. 1954. Motivation and Personality. ed. Gardner Murphy. New York, NY: Harper & Bros.
Mayo, Deborah G. 2005. “Peircean Induction and the Error-Correcting Thesis”. Transactions of the Charles S. Peirce Society 41, no. 2: 299–319.
Mayr, Ernst, Gorton Linsley and Robert L. Usinger. 1953. Methods and Principles of Systematic Zoology. New York: McGraw-Hill.
Mayr, Ernst. 1982. The Growth of Biological Thought: Diversity, Evolution, and Inheritance. Cambridge, Mass: Belknap Press.
Mazzocchi, Fulvio. 2013. “Images of Thought and Their Relation to Classification: The Tree and the Net”. Knowledge Organization 40, no. 6: 366-74.
McGuinness, Deborah L. and Alex Borgida. 1995. “Explaining Subsumption in Description Logics”. In
Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, Quebec, ed. Ron Kohavi. Morgan Kaufmann: 816-21.
Michel, Dee. 1997. “Appendix B: Taxonomy of Subject Relationships”. In Final Report to the ALCTS/CCS Subject Analysis Committee, ALA Report, ed. J. Greenberg. American Library Association, 18.
Midtgarden, Torjus. 2019. “Peirce’s Classification of the Sciences”. ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/peirce.
Miksa, Francis. 1994. “Classification”. In Encyclopedia of Library History, eds. Wayne A. Wiegand and Donald G. Davis, Jr. New York: Garland Publishing, 144-53.
Miller, David, Tony Olson, and Sara Shatford Layne. 2005. “Promoting Research and Best Practices in Subject Reference Structures”. Library Resources & Technical Services 49, no. 3: 154–66.
Miller, George A. 1995. “WordNet: A Lexical Database for English”. Communications of the ACM 38, no. 11: 39–41.
Napoli, Amedeo. 1995. “Objects, Classes, Specialization and Subsumption”. In Proceedings of the 1995 International Workshop on Description Logics, University of Rome, June 2-3, 1995 (Technical Report 07.95), eds. Alex Borgida, Maurizio Lenzerini , Daniele Nardi and Bernhard Nebel. Rome: University of Rome: 52–55. http://citeseerx.ist.psu.edu/....
Needham, Joseph. 1937. “Integrative Levels: A Revaluation of the Idea of Progress”. In Time: The Refreshing River (Essays and Addresses, 1932-1942), Herbert Spencer Lecture at Oxford University. London, UK: George Allen & Unwin Ltd., 233–72. https://archive.org/details/timerefreshingri00need/page/232/mode/2up (March 6, 2020).
Newman, Phil. 2013. “Discovering the Electromagnetic Spectrum”. NASA Goddard Space Flight Center. https://imagine.gsfc.nasa.gov/science/toolbox/history_multiwavelength1.html (March 14, 2020).
Nilsson, Jørgen Fischer. 2006. “Ontological Constitutions for Classes and Properties”. In Conceptual Structures: Inspiration and Application. Lecture Notes in Computer Science, eds. Henrik Schärfe, Pascal Hitzler, and Peter Øhrstrøm. Aalborg, Denmark: Springer, 35–53.
Olson, H. A. 1999. “Exclusivity, Teleology and Hierarchy: Our Aristotelean Legacy”. Knowledge Organization 26, no. 2: 65–73.
Oxford English Dictionary: The Definitive Record of the English Language. (OED). Oxford, UK: Oxford University Press. OED online: https://www.oed.com/ (Toll access; visited 2021-01-29).
Padgham, Lin, and Patrick Lambrix. 1994. “A Framework for Part-of Hierarchies in Terminological Logics”. In Principles of Knowledge Representation and Reasoning, eds. Bernhard Nebel, Charles Rich, and William Swartout. San Mateo, CA: Elsevier, 485–96.
Paine, Rainer W., and Jun Tani. 2005. “How Hierarchical Control Self-Organizes in Artificial Adaptive Systems”. Adaptive Behavior 13, no. 3: 211–25.
Parker, Kelly A. 1998. The Continuity of Peirce’s Thought. Nashville: Vanderbilt University Press.
Parry, William T. and Edward A. Hacker. 1991. Aristotelian Logic. New York, NY: State University of New York Press.
Patrides, Constantinos A. 1974. “Hierarchy and Order”. In Dictionary of the History of Ideas: Studies of Selected Pivotal Ideas, Volume II (Despotism - Law, Common), ed. Philip P. Wiener. New York, NY: Scribner. http://xtf.lib.virginia.edu/....
Pattee, Howard H. 1973a. “Postscript: Unsolved Problems and Potential Applications of Hierarchy Theory”. In Hierarchy Theory: The Challenge of Complex Systems, ed. Howard H. Pattee. New York, NY: George Brazilller, 131–56.
Pattee, Howard H. 1973b. “The Physical Basis and Origin of Hierarchical Control”. In Hierarchy Theory: The Challenge of Complex Systems, ed. Howard H. Pattee. New York, NY: George Brazilller, 72–108.
Peirce, Charles Sanders. 1867. “Upon Logical Comprehension and Extension”. In Proceedings of the American Academy of Arts and Sciences, ed. American Academy of Arts and Sciences. Metcalf and Company, 416–32.
Peirce, Charles Sanders. 1877. “The Fixation of Belief”. Popular Science Monthly 12, no. 1: 1–15.
Peirce, Charles Sanders. 1891. “The Architecture of Theories”. The Monist 1, no. 2: 161–76.
Peirce, Charles Sanders. 1905a. “Issues of Pragmaticism”. The Monist 15, no. 4: 481–99.
Peirce, Charles Sanders. 1905b. “What Pragmatism Is”. The Monist 15, no. 2: 161–81.
Peirce, Charles Sanders. 1906. “Prolegomena to an Apology for Pragmaticism”. The Monist 16, no. 4: 492–546.
Peirce, Charles Sanders. 1931. The Collected Papers of Charles Sanders Peirce, 8 Volumes. eds. Charles Hartshorne, Paul Weiss, and Arthur W Burks. Cambridge, MA: Harvard University Press.
Peirce, Charles Sanders. 1976. The New Elements of Mathematics. Four vols. (in five books), ed. Carolyn Eisele. The Hague: Mouton.
Peirce, Charles Sanders. 1992a. “The Logic of Continuity”. In Reasoning and the Logic of Things: The Cambridge Conferences Lectures of 1898, ed. Kenneth Laine Ketner. Harvard University Press, 242–63.
Peirce, Charles Sanders. 1992b. “Types of Reasoning”. In Reasoning and the Logic of Things: The Cambridge Conferences Lectures of 1898, ed. Kenneth Laine Ketner. Harvard University Press, 121–42.
Peirce, Charles Sanders. 1997. Pragmatism as a Principle and Method of Right Thinking: The 1903 Harvard Lectures on Pragmatism, ed. Patricia Ann Turrisi. State University of New York Press.
Peirce, Charles Sanders. 1998a. “An Outline Classification of the Sciences”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 258–62.
Peirce, Charles Sanders. 1998b. “On Science and Natural Classes”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 115–32.
Peirce, Charles Sanders. 1998c. “On the Logic of Drawing History from Ancient Documents, Especially the Testimonies”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 75–114.
Peirce, Charles Sanders. 1998d. “Pragmatism”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 398–433.
Peirce, Charles Sanders. 1998e. “Sundry Logical Conceptions”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 269–88.
Peirce, Charles Sanders. 1998f. “The Basis of Pragmaticism in the Normative Sciences”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 371–97.
Peirce, Charles Sanders. 1998g. The Essential Peirce: Selected Philosophical Writings, Vol 2 (1893-1913). ed. Peirce Edition Project. Bloomington, Indiana: Indiana University Press.
Peirce, Charles Sanders. 1998h. “The Neglected Argument for the Reality of God”. In The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913), ed. The Peirce Edition Project. Bloomington, Indiana: Indiana University Press, 434–50.
Pellegrin, Pierre. 1986. Aristotle's Classification of Animals: Biology and the Conceptual Unity of the Aristotelian Corpus. (Translated from “Classification des animaux chez Aristote: Statut de la biologie et unité de l'aristotélisme» (Paris, Les Belles Lettres, 1982) by Anthony Preus. Berkeley: University of California Press.
Plato. 1925. Phaedrus, Section 265e”. http://www.perseus.tufts.edu/... (December 28, 2020).
Potochnik, Angela, and Brian McGill. 2012. “The Limitations of Hierarchical Organization”. Philosophy of Science 79, no. 1: 120–40.
Pumain, Denise. 2006. “Introduction”. In Hierarchy in Natural and Social Sciences, ed. Denise Pumain. Dordrecht: Springer Netherlands, 1–12. https://link.springer.com/chapter/10.1007/1-4020-4127-6_1 (March 1, 2020).
Quammen, David. 2018. The Tangled Tree: A Radical New History of Life. London: William Collins.
Quinn, Aleta. 2017. “When Is a Cladist Not a Cladist?” Biology & Philosophy 32, no. 4: 581–98.
Roche, Christophe. 2016. “Should Terminology Principles Be Re-Examined?” arXiv:1609.05170 [cs]. http://arxiv.org/abs/1609.05170 (December 30, 2020).
Salthe, Stanley N. 2002. “Summary of the Principles of Hierarchy Theory”. General Systems Bulletin 31: 13–17.
Salthe, Stanley N. 2009. “A Hierarchical Framework for Levels of Reality: Understanding Through Representation”. Axiomathes 19, no. 1: 87–99.
Salthe, Stanley N. 2011. “Naturalizing Information”. Information 2, no. 3: 417–25.
Salthe, Stanley N. 2012. “Hierarchical Structures”. Axiomathes 22, no. 3: 355-83.
Shannon, Claude E. 1948. “A Mathematical Theory of Communication”. Bell System Technical Journal 27, no. 3: 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
Shapley, Harlow. 1958. Of Men and Stars: Human Response to an Expanding Universe. Boston, MA: Beacon Press.
Short, Thomas Lloyd. 2007. Peirce’s Theory of Signs. Cambridge University Press.
Simon, Herbert A. 1962. “The Architecture of Complexity”. Proceedings of the American Philosophical Society 105, no. 6: 467–82.
Sluys, Ronald, Koen Martens and Frederick R. Schram. 2004. “The PhyloCode: Naming of Biodiversity at a Crossroads”. Trends in Ecology and Evolution 19, no. 6: 280-1. DOI: 10.1016/j.tree.2004.04.001cal.
Snyder, Steve. 2014. “The Great Chain of Being”. Grand View University Faculty Pages. https://web.archive.org/web/20170728101006/http://faculty.grandview.edu/ssnyder/121/121 great chain.htm.
Solskinnsbakk, Geir et al. 2010. “Quality of Subsumption Hierarchies in Ontologies”. In Natural Language Processing and Information Systems, eds. Helmut Horacek, Elisabeth Métais, Rafael Muñoz, and Magdalena Wolska. Berlin, Heidelberg: Springer Berlin Heidelberg, 258–68. https://link.springer.com/chapter/10.1007/978-3-642-12550-8_21 (February 20, 2020).
Sørlie, Therese et al. 2001. “Gene Expression Patterns of Breast Carcinomas Distinguish Tumor Subclasses with Clinical Implications”. Proceedings of the National Academy of Sciences 98, no. 19: 10869–74.
Sowa, John. 2001. “Glossary”. Ontology. http://www.jfsowa.com/ontology/gloss.htm (February 23, 2020).
Spiliopoulos, Vassilis, George A. Vouros, and Vangelis Karkaletsis. 2010. “On the Discovery of Subsumption Relations for the Alignment of Ontologies”. Journal of Web Semantics 8, no. 1: 69–88.
Stoica, Emilia, and M. Hearst. 2004. “Nearly-Automated Metadata Hierarchy Creation”. HLT-NAACL ‘04, Companion Volume. http://acl.ldc.upenn.edu/hlt-naacl2004/shorts/pdf/253_Paper.pdf.
Stoica, Emilia, Marti A. Hearst, and Megan Richardson. 2007. “Automating Creation of Hierarchical Faceted Metadata Structures”. In Human Language Technologies 2007, Proceedings of the Main Conference. Rochester, NY: Association for Computational Linguistics, 244–51.
Stumme, Gerd. 1999. “Hierarchies of Conceptual Scales”. In Proceedings of the 12th Workshop on Knowledge Acquisition, Modeling and Management (KAW'99), eds. T. B. Gaines, R. Kremer and M. Musen. Banff, volume 2: 78–95.
Tobin, Emma. 2010. “Crosscutting Natural Kinds and the Hierarchy Thesis”. In The Semantics and Metaphysics of Natural Kinds, eds. Helen Beebee and Nigel Sabbarton-Leary. New York, NY: Routledge, 187–99. https://www.taylorfrancis.com/books/9780203852330.
Van Hove, Alphonse. 1910. “Hierarchy”. In Catholic Encyclopedia. New York: Robert Appleton Company. Retrieved from New Advent: http://www.newadvent.org/cathen/07322c.htm (January 22, 2021).
Vasilyeva, Larissa N., and Steven L. Stephenson. 2008. “The Linnaean Hierarchy and ‘Extensional Thinking’”. The Open Evolution Journal 2, no. 1: 55–65. https://benthamopen.com/DOWNLOAD-PDF/TOEVOLJ-2-55/ (January 22, 2021).
Verdier, Nicolas. 2006. “Hierarchy: A Short History of a Word in Western Thought”. In Hierarchy in Natural and Social Sciences, ed. Denise Pumain. Dordrecht: Springer Netherlands, 13–37. https://link.springer.com/chapter/10.1007/1-4020-4127-6_2 (March 1, 2020).
W3C. 2008. “Vocabularies”. W3C Standards - Semantic Web. https://www.w3.org/standards/semanticweb/ontology (March 15, 2020).
Walker, Sara Imari. 2014. “Top-Down Causation and the Rise of Information in the Emergence of Life”. Information 5, no. 3: 424–39.
Walker, Sara Imari, and Paul C. W. Davies. 2013. “The Algorithmic Origins of Life”. Journal of The Royal Society Interface 10, no. 79: 1-9. https://doi.org/10.1098/rsif.2012.0869.
Wilkins, John S. and Malte C. Ebach. 2014. The Nature of Classification: Relationships and Kinds in the Natural Sciences. New York: Palgrave MacMillan.
Wille, Rudolf. 1995. “The Basic Theorem of Triadic Concept Analysis”. Order 12, no. 2: 149–58.
Wilson, Donna M. 1968. “Forms of Hierarchy: A Selected Bibliography”. In Hierarchical Structures: Proceedings of a Symposium, Douglas Advanced Research Laboratories, eds. Lancelot Law Whyte, Albert George Wilson, and Donna M. Wilson. Douglas Advanced Research Laboratories, Huntington Beach, CA: Elsevier Publishing Company, 287–314.
Wimsatt, William C. 1972. “Complexity and Organization”. In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association. Dordrecht: D. Reidel Publishing, 67–86. https://www.jstor.org/stable/3698961.
Witteveen, Joeri. 2020. “Linnaeus, the Essentialism Story, and the Question of Types”. Taxon 69, no. 6: 1141-9. DOI https://doi.org/10.1002/tax.12346.
WordNet 3.1: A Lexical Database for English. http://wordnetweb.princeton.edu/perl/webwn (Visited 2021-01-29).
Wu, Jianguo. 2013. “Hierarchy Theory: An Overview”. In Linking Ecology and Ethics for a Changing World, eds. Ricardo Rozzi et al. Dordrecht: Springer Netherlands, 281–301. http://link.springer.com/10.1007/978-94-007-7470-4_24 (February 22, 2020).
Yao, Yiyu. 2009. “Integrative Levels of Granularity”. In Human-Centric Information Processing Through Granular Modelling, eds. Andrzej Bargiela and Witold Pedrycz. Berlin: Springer Science & Business Media, 31–48.
Zadeh, Lotfi Asker. 1971. “Similarity Relations and Fuzzy Orderings”. Information Sciences: An International Journal 3, no. 2: 177–200. https://doi.org/10.1016/S0020-0255(71)80005-1.
Zalamea, Fernando. 2003. “Peirce’s Logic of Continuity: Existential Graphs and Non-Cantorian Continuum”. The Review of Modern Logic 9, no. 1–2: 115–62.
Zalamea, Fernando. 2012. Peirce’s Continuum: A Methodological and Mathematical Approach. Boston, MA: Docent Press.
Zalamea, Fernando. 2013. “Plasticity and Creativity in the Logic Notebook”, eds. Mats Bergman and Sami Paavola. European Journal of Pragmatism and American Philosophy 5, no. 1: 1-14. http://journals.openedition.org/ejpap/593 (January 1, 2021).
Zeng, Marcia Lei. 2005. “Construction of Controlled Vocabularies, a Primer (Based on Z39. 19)”. Based on ANSI/NISO Z39.19-2005: Guidelines for the Construction, Format, and Management of Monolingual Controlled Vocabularies 3919. https://marciazeng.slis.kent.edu/Z3919/index.htm.
Appendix: Some definitions related to hierarchy in ISO standards
ISO 5127: 2017, definition 3.1.7.01: “semantic relation (semantic relationship): relation (3.1.1.12) between concepts (3.1.1.02) and between class (3.8.5.03) symbols (3.1.4.17) and their meanings (3.1.8.03)”.
ISO 5127: 2017, definition 3.1.7.12: “hierarchical relation: semantic relation (3.1.7.01) between a pair of concepts (3.1.1.02) of which one has a scope falling completely within the scope of the other”.
ISO 25964-1: 2011, Section 10.2 writes: “The hierarchical relationship should be established between a pair of concepts when the scope of one of them falls completely within the scope of the other. It should be based on degrees or levels of superordination and subordination, where the superordinate concept represents a class or whole, and subordinate concepts refer to its members or parts”. And: “The hierarchical relationship may be one of three types, corresponding to three logically different situations as follows:
a) the generic relationship.
b) the hierarchical whole-part relationship.
c) the instance relationship.
Each of these leads to hierarchies which are amenable to a logical test through reference to the types of concept involved”.
ISO 5127: 2017, definition 3.1.7.05: “generic relation: relation (3.1.1.12) between two concepts (3.1.1.02) where the intension (3.1.2.24) of one of the concepts includes that of the other concept and at least one additional delimiting characteristic (3.1.1.04).
ISO 25964-1: 2011, Section 10.2.2 writes: “The generic relationship is the link between a class or category and its members or species. In addition to the test for validity described in 10.2.1, this relationship is also amenable to a logical "all and-some test" [… Some birds are parrots and all parrots are birds satisfy the all-and-some test, whereas some pets are parrots and some parrots are pets do not satisfy the definition of the generic relation, but exceptions may apply to a specialist thesaurus devoted to domestic animals]”.
ISO 5127: 2017, definition 3.1.7.06: “partitive relation (part-whole relation): relation (3.1.1.12) between two concepts (3.1.1.02) where one of the concepts constitutes the whole and the other concept a part of that whole”.
ISO 25964-1: 2011, Section 10.2.3 writes (examples omitted): “The hierarchical whole-part relationship covers a limited range of situations in which a part of an entity or system belongs uniquely to a particular possessing whole. This applies to four main classes of terms: “a) systems and organs of the body; b) geographical locations; c) disciplines or fields of discourse; d) hierarchical social structures.
Most other cases of the whole-part relationship are not eligible for a hierarchical linkage because the part could belong to more than one whole. For example, a BT/NT relationship should not be established between "bicycles" and "wheels" because a wheel may be part of a motor car or a wheelbarrow or many other artefacts. An exploded search for bicycles would retrieve much unwanted material if it were extended to all types of wheel. It is sometimes the case, however, that the parts of an artefact are unique to that artefact, at least in the field of application of the thesaurus”.
ISO 5127: 2017, definition 3.1.7.09: “instance relationship (instantive relationship): relationship (3.1.1.12) between a general concept (3.1.2.15) such as a class (3.8.5.03) of things or events, and an individual instance (3.1.13.28) of that class, which is often represented by a proper name (3.1.5.28)”.
ISO 25964-1: 2011, Section 10.2.4 writes: “The instance relationship links a general concept such as a class of things or events, and an individual instance of that class, often represented by a proper name”.
ISO 25964-1: 2011, Section 10.2.5 writes: “Some concepts can belong, on logical grounds, to more than one group or class at the same time, in which case they are said to possess polyhierarchical relationships”. (The term organs, for example, has both keybord instruments and wind instruments as generic broader terms; the term biochemistry has both biology and chemistry as whole-part broader terms; the term skull is both a kind of bones and a part of head, thus forming a polyhierarchical with mixed kinds of relations).
Version 1.0 published 2021-02-21
Article category: Core concepts in KO
This article (version 1.0) is also published in Knowledge Organization. How to cite it:
Bergman, Michael K. 2022.
“Hierarchy in knowledge systems”.
Knowledge Organization 49, no. 1: 40-66.
Also available in
ISKO Encyclopedia of Knowledge Organization,
eds. Birger Hjørland and Claudio Gnoli,
https://www.isko.org/cyclo/hierarchy
©2021 ISKO. All rights reserved.