I S K O
Encyclopedia of Knowledge Organization
Classification of the sciences in Greco-Roman antiquity
by Jonathan FurnerTable of contents:
1. Introduction
2. The Pre-Socratic period (c. 600–400 BCE): 2.1 Pythagoras of Samos (c. 570 – c. 495 BCE); 2.2 Protagoras of Abdera (c. 490 – c. 420 BCE); 2.3 Hippocrates of Chios (fl. c. 440 BCE); 2.4 Theodorus of Cyrene (fl. late 5th Century BCE); 2.5 Hippias of Elis (fl. late 5th Century BCE); 2.6 Philolaus of Croton (c. 470 – c. 385); 2.7 Archytas of Tarentum (fl. early 4th Century BCE)
3. The Classical period (c. 400–300 BCE): 3.1 Isocrates (436–338 BCE); 3.2 Plato (428/427 – 348/347 BCE); 3.3 Speusippus of Athens (c. 408 – 339/338 BCE); 3.4 Xenocrates of Chalcedon (c. 396/395 – 314/313 BCE); 3.5 Aristotle (384–322 BCE)
4. The Hellenistic period (c. 300–150 BCE): 4.1 Epicurus (341–270 BCE); 4.2 Zeno of Citium (c. 334 – c. 262 BCE); 4.3 Cleanthes of Assos (c. 330 – c. 230 BCE); 4.4 Callimachus of Cyrene (c. 305 – c. 240 BCE); 4.5 Chrysippus of Soli (c. 279 – c. 206 BCE)
5. The Roman period (c. 150 BCE – 250 CE): 5.1 Dionysius Thrax (c. 170 – c. 90 BCE); 5.2 Posidonius of Apamea (c. 135 – c. 51 BCE); 5.3 Geminus (fl. 1st Century BCE); 5.4 Marcus Terentius Varro (116–27 BCE); 5.5 Marcus Tullius Cicero (106–43 BCE); 5.6 Philo of Alexandria (c. 15 BCE – 45 CE); 5.7 Gaius Plinius Secundus (23/24 – 79); 5.8 Marcus Fabius Quintilianus (c. 35 – c. 100); 5.9 Plutarch (c. 46 – c. 120); 5.10 Theon of Smyrna (fl. c. 100); 5.11 Nicomachus of Gerasa (fl. c. 150); 5.12 Galen (129 – c. 216); 5.13 Sextus Empiricus (c. 160 – c. 210); 5.14 Flavius Philostratus (c. 170 – c. 250); 5.15 Plotinus (c. 204 – 270)
6. Late Antiquity (c. 250–600): 6.1 “Maximus Victorinus” (4th Century?); 6.2 Augustine of Hippo (354–430); 6.3 Martianus Minneus Felix Capella (fl. c. 410–420); 6.4 Anicius Manlius Severinus Boëthius (c. 477 – 524); 6.5 Flavius Magnus Aurelius Cassiodorus Senator (490 – c. 585); 6.6 Isidore of Seville (c. 560 – 636)
7. Analysis
8. Conclusion
Acknowledgments
Endnotes
References
ColophonAbstract:
A review is undertaken of the contributions of 38 classical authors, from Pythagoras in the 6th Century BCE to Isidore in the 6th Century CE, to the classification of the sciences. Such classifications include some that are more theoretical in function, some that are more practical (e.g., encyclopedic, bibliographic, or curricular). The emergence of the quadrivium and trivium is charted; the Greek concept of enkýklios paideía and the Latin term artēs liberales are defined; and the ways in which the form, content, and function of science classifications change during this period are assessed.
1. Introduction
For the purposes of this IEKO entry, Greco-Roman antiquity is defined as the 1,400-year period of cultural history centered on the Mediterranean Sea between 800 BCE and 600 CE. Of course, this period was particularly notable for the rise and subsequent dissolution of the civilizations of ancient Greece and ancient Rome, and for the emergence of Christianity; but the length of the period and the breadth of the territory means that a wide variety of cultures are covered. The ways in which those cultures have been interpreted in later times have significantly shaped interpreters’ understandings of themselves: “Every domain of post-classical life and thought has been profoundly influenced by ancient models. [...] One cannot understand the history of the post-classical world without constant reference to the classical cultures by which it has never ceased to define itself — in assent and dissent, in defiance and imitation, in veneration and in willed but futile forgetfulness” (Grafton, Most and Settis 2010, vii). It is hoped that the survey of ancient systems for the classification of the sciences provided in this entry suggests some ways of improving our understanding of the systems with which we are more familiar in the present day.
It might seem presumptuous to attempt to summarize more than a millennium’s worth of scholarly activity in a few pages, but we judge it to be worth a try for two reasons: firstly, there does exist an (until very recently, somewhat moribund) disciplinary context in which the present IEKO entry roughly fits (see, e.g., Flint 1904; Richardson 1930; Fisher 1990; Sandoz 2018); and secondly, it is not as if the intention here is to cover all ancient work on the construction of (what are known in modern times as) → ontologies and taxonomies.
To elaborate on this second point:
- In his Isagoge (Introduction [to logic]), Porphyry of Tyre (c. 234 – c. 305) provided a commentary on Aristotle’s work that lent itself to visualization in the form of the so-called Tree of Porphyry, an illustration of the logic of taxonomic → division that became popular in textbooks of the Middle Ages (Verboon 2014).
- In his Categories, Aristotle (384–322 BCE) famously expressed ideas about the identity and nature of the fundamental categories of things in the world (Studtmann 2013), producing a top-level ontology avant la lettre (cf., e.g., Smith 2003).
- Similarly, in his History of Animals, Aristotle the biologist classified animals into two groups (those with and those without blood), divided the groups into genera, and identified about 500 different species (Pellegrin 1986).
In this IEKO entry, though, we are not concerned with ontology, at least not in the narrow sense in which that term is used in the information sciences to refer to the production of conceptual models. In other words, we will not be looking at examples of schemes for the classification of words, concepts, or real-world entities in general. Neither are we concerned with taxonomy, historically conceived as the systematic classification of living organisms. We will not be looking at examples of schemes for the classification of kinds of entities such as plants or animals, nor (by extension) those for minerals or human-made artefacts (other than a few special sorts listed below).
Instead, we are deliberately limiting the coverage to schemes for the classification specifically of sciences, broadly defined in this case to include systems for classifying the following:
- → disciplines, fields, subjects;
- areas of inquiry, study, teaching;
- branches of knowledge, learning, education.
The Ancient Greek word ἐπιστήμη / epistēmē is often translated as “knowledge”, sometimes as “theory” or “science”; the plural form ἐπιστήμαι / epistḗmai is usually translated as “the sciences”. Similarly, τέχνη / tékhnē is often translated as “art”, sometimes as “practice” or “craft”; the plural form τέχναι / tékhnai is usually translated as “the arts”. But this summary presents a cleaner distinction than is warranted by actual Greek usage (Parry 2020). As Tatarkiewicz (1963, 235) points out, “the difference between sciences and arts was in antiquity always vague and indefinite”. Whitney (1990, 25, n. 7) elaborates: “The Greek term for art (τέχνη) and its Latin equivalent (ars) were used broadly to apply to virtually all human activities which were in some sense rational, including what we would now distinguish as science, fine art and technology”. Consequently, it would be difficult, and in any case undesirable, to limit our survey of classifications of the sciences so that it did not also include instances of classifications of the arts. Examples of both kinds of classification are included, alongside schemes for the division of important individual disciplines such as philosophy and mathematics.
That there is some value in conducting the present study is perhaps indicated by the quantity of material that has been compiled for inclusion in the entry. The main body is intended as an updated and augmented version of the annotated list provided in Richardson’s Classification: Theoretical and Practical (Richardson 1930). Richardson splits his list into two: the “Theoretical Systems” (Richardson 1930, 48–88) that have been developed primarily by philosophers and encyclopedists, and the “Practical Systems” (Richardson 1930, 88–149) that have been developed primarily by librarians and bibliographers for the classification of the subjects of library resources such as books [1]. To the second category we may wish to add systems that have been developed by educators and scholars for the classification of the areas of study that form school, college, and university curricula. Since it is often difficult, in practice, to draw a precise line between “theoretical” and “practical” systems, we propose to treat systems of all kinds — philosophical and encyclopedic, bibliographic and curricular — in a single chronologically-arranged but otherwise undifferentiated inventory.
As well as Richardson’s 1930 book, five other texts were used as main sources of names of ancient classificationists deserving coverage in the sections following below:
- the 1955 book Очерки по истории библиотечно-библиографической классификации, vol. 1 [Essays on the history of library-bibliographic classification; trans. into German in 1964 as Geschichte der bibliothekarisch-bibliographischen Klassifikation, vol. 1], by Evgenij Ivanovic Šamurin (1889–1962);
- the 1963 paper “Classification of Arts in Antiquity” by Władysław Tatarkiewicz (1886–1980);
- the 1965 paper “Classification of the Sciences in Medieval Thought” by James A. Weisheipl (1923–1984);
- the 1990 paper “Liberal and Illiberal Arts: The Classification of Technical Arts in Antiquity” by Elspeth Whitney; and
- the 2018 website Interactive Historical Atlas of the Disciplines by Raphaël Sandoz.
Table 1 lists the ancient authors whose classificatory work is covered by each of these texts and by the present survey.
Table 1: Coverage of ancient authors in seven texts
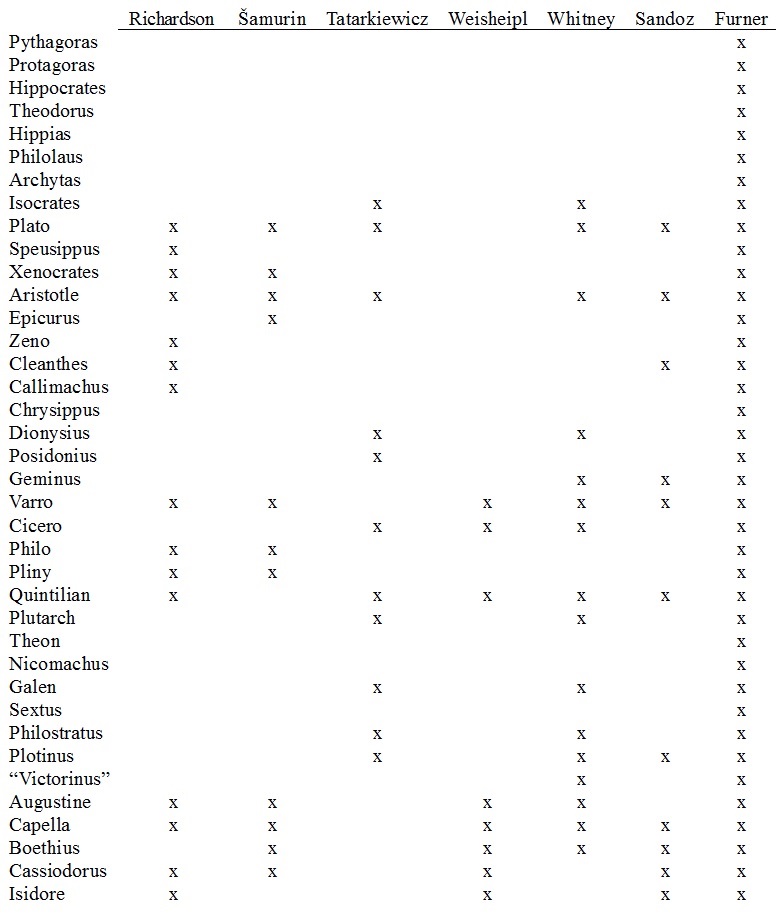
The bulk of Greek and Roman philosophical texts have been lost. The extant works of Plato and Aristotle are notable for being more or less complete, but we are not so lucky with respect to most other philosophers. Our knowledge of lost works, such as it is, derives from surviving writings by other authors that contain commentary on the lost originals. (The 19th-Century term for a collection of such secondary sources is doxography; the doxographical tradition comprises a succession of collections of comments on, opinions on, and in some cases excerpts from original texts. See, for example, Mansfeld (2016).) Occasionally, as in the case of Plato and Aristotle, we enjoy access both to surviving originals and surviving commentary. In all cases, we must be careful to distinguish original from commentary, since the trustworthiness of the latter as evidence of the ideas of authors of the former is decidedly less. Two authors in whose oeuvres we should tread particularly carefully are the Pyrrhonist skeptic Sextus Empiricus and the biographer Diogenes Laertius. In his writings, Sextus Empiricus (c. 160 – c. 210) rails against other philosophies to such an extent that his works amount to a major source of information about those philosophies. Diogenes Laertius (fl. 3rd Century) wrote Lives of the Eminent Philosophers in ten books — still an important source of lore on ancient Greek philosophers, notwithstanding persistent doubts as to its reliability.
The basic rationale for undertaking a survey such as this is that ancient classifications of the sciences both (A) served as the foundations for schemes developed in the medieval and early modern periods, and (B) continue to exert an influence on our thinking about classification today. To understand classifications of the present, it is necessary to know as much as possible about classifications of the past — even (one might say, especially) the ancient past. As Whitney (1990, 24) argues, “the ways in which thinkers organize knowledge are extremely revealing of fundamental attitudes about the nature and value of the different arts and sciences which together make up the sum total of that knowledge”. We will have more to say in a later section about our major findings (see Section 7, below); but, as a guide as to what to look out for as we move through the centuries, a brief statement of the concerns of those findings appears here:
- the division of mathematics into four subjects known collectively as the quadrivium;
- the division of philosophy into logic, physics, and ethics;
- the classification of sciences into theoretical, practical, and productive;
- a curriculum of “liberal arts” consisting of the quadrivium alongside what would later be known as the trivium;
- attempts to merge quadrivium/trivium-based classifications with the tripartite division of philosophy; and
- an increasing complexity in classification schemes over the period of the survey.
Meanwhile, classification in general is covered in a separate IEKO entry by Hjørland on → classification (see also Hjørland 2017); → library classification and its premodern history in particular by Dousa.
2. The Pre-Socratic period (c. 600–400 BCE)
2.1 Pythagoras of Samos (c. 570 – c. 495 BCE)
At some point in classical history — the rough timing of which is to be discussed below — the four areas of study known as arithmetic (a.k.a. calculation, number, or logistic), geometry (both plane and solid), astronomy (a.k.a. astrology or spherics), and music (a.k.a. harmonics or acoustics) came to be (A) treated as a group, related to one another in virtue of the similarity of their mathematical foundations, and (B) recommended collectively as the components of a curriculum for teaching and learning that eventually came to be known by the Latin term quadrivium (“the four-way crossroads”). Such a curriculum has been ascribed to Plato, among others: “Plato [...] followed the traditional Pythagorean quadrivium”, says Marrou (1956, 75); Kahn (2001, 40) concurs that “the mathematical curriculum of [Plato’s] Republic is directly based on the Pythagorean quadrivium”. We shall examine these claims in the context of Plato’s work later; our present task is to consider the qualifier “Pythagorean” and to determine whether it refers specifically to Pythagoras (as, at first sight, it may appear to), or more generally to any group of precursors, collaborators, or followers. When Kahn (2001, 13) asserts that “[t]he medieval quadrivium is [...] authentically Pythagorean”, what does he mean?
Pythagoras was a Greek philosopher from the 6th and early 5th Centuries BCE (see, e.g., Huffman 2018). He wrote nothing, which has made it difficult to reach definitive conclusions about his work. His renown in the modern world is as a mathematician and scientist, responsible (or so tradition has it) for the discovery of (A) an eponymous theorem about the three sides of a right triangle, (B) a correspondence between the basic concords in music (octave, fifth, and fourth) and the ratios that can be expressed using the first four whole numbers (2:1, 3:2, and 4:3), and (C) a model of the cosmos in which the movements of the heavenly bodies produce music, the so-called “harmony of the spheres”.
As a consequence, Pythagoras has come to be popularly credited with improving our understanding of the relationships between the four subjects of the quadrivium. Yet “[i]t remains controversial [...] whether he was in any sense a mathematician” (Huffman 2018) — or even, for that matter, a scientist. In his examination of “the most fundamental evidence of all” — i.e., “the testimony of authors [who] precede [...] Aristotle” — Huffman (2018) finds nothing to demonstrate Pythagoras’s expertise in any area of mathematics. Instead, Pythagoras is presented primarily as the founder of a certain way of life — one that emphasized the proper observance of traditional Greek religious ritual, and that prepared the soul for life after death. Pythagoras may well have believed that the world is structured in accordance with mathematical regularities, and may well have attributed great significance to the mathematical relationships inherent in discoveries of the kinds for which he is celebrated. But it is likely that others were responsible for those discoveries: the Babylonians in the case of “Pythagoras’s” theorem (see, e.g., Lloyd 2014, 34–35), instrument-makers in the case of the concord/ratio correspondences (see, e.g., Barker 2014, 202).
The explicit identification of the quadrivium as a way of organizing knowledge for study, then, is not a development that should be attributed to Pythagoras as an individual. Instead, the sense of “Pythagorean” that is indicated in formulations such as “Pythagorean quadrivium” is one that relates to both precursors and followers of Pythagoras, as we shall see below.
2.2 Protagoras of Abdera (c. 490 – c. 420 BCE)
Protagoras was one of the first of the sophists, a new profession of itinerant teachers established in the 5th Century BCE (see, e.g., Taylor and Lee 2015). He is perhaps best known for the dictum “Man is the measure of all things” (ascribed by Socrates to Protagoras in Plato’s Theaetetus), a claim that (in Theaetetus’s words) “knowledge is nothing but perception” (Plato 1961b, 856, paras. 151e–152a).
In Plato’s Protagoras, Protagoras is quoted as follows: “When he comes to me, Hippocrates [of Cos, the physician, c. 460 – 370 BCE] will not be put through the same things that another Sophist would inflict on him. The others treat their pupils badly; these young men, who have deliberately turned their backs on specialization, they take and plunge into special studies again, teaching them arithmetic and astronomy and geometry and music — here he glanced at Hippias [of Elis; see below, Section 2.5] — but from me he will learn only what he has come to learn” (Plato 1961a, 317, para. 318d–e [emphases added]). Here Protagoras is contrasting the practical education which he himself offers with the quadrivium offered by other sophists, Hippias in particular. Just as we may consider it unlikely that Pythagoras was the first to organize study or teaching along the lines of the quadrivium, neither should Protagoras be treated as a credible candidate. (Hippias, on the other hand, is one to bear in mind.)
2.3 Hippocrates of Chios (fl. c. 440 BCE)
Hippocrates of Chios — not to be confused with Hippocrates of Cos, the physician — was a Greek geometer and astronomer (see, e.g., Lloyd 1987). He compiled the first known work on the elements of geometry, which is unfortunately no longer extant. The achievements in mathematics of Archytas of Tarentum (see below, Section 2.7) “depend on the work of Hippocrates” (Huffman 2016b), although there is no evidence that Archytas studied with Hippocrates himself, nor that Hippocrates consciously organized his teaching in terms of the quadrivium.
2.4 Theodorus of Cyrene (fl. late 5th century BCE)
Theodorus was a Libyan Greek geometer and teacher, about whose life in the 5th Century BCE little is known. In Plato’s Theaetetus, however, Theodorus is said to be knowledgeable in calculation/arithmetic, geometry, astronomy, and music/harmonics, and to be teaching these subjects to Theaetetus:
Socrates: Well, is Theodorus a painter?
Theaetetus: Not so far as I know.
Socrates: Nor an expert in geometry either?
Theaetetus: Of course he is, Socrates, very much so.
Socrates: And also in astronomy and calculation and music and in all the liberal arts?
Theaetetus: I am sure he is.
[...]
Socrates: Tell me, then, you are learning some geometry from Theodorus?
Theaetetus: Yes.
Socrates: And astronomy and harmonics and arithmetic?
Theaetetus: I certainly do my best to learn.
(Plato 1961b, 849–850, para. 145a,c–d [emphases added]).
The components of the quadrivium will be recognized. Notwithstanding the lack of additional evidence, Theodorus may thus be considered one of the earliest adherents of this way of organizing a curriculum.
Theodorus’s curriculum (according to Plato):
- Geometry
- Astronomy
- Calculation / Arithmetic
- Music / Harmonics
2.5 Hippias of Elis (fl. late 5th Century BCE)
Hippias was a Greek sophist in the 5th Century BCE (see, e.g., Sutton 2005). Marcus Tullius Cicero’s testimony in the 1st Century BCE is that Hippias was a teacher of great versatility: in Cicero’s De oratore, Quintus Lutatius Catulus (149–87 BCE) says that Hippias had “boasted [...] that there was not a single fact included in any system of encyclopaedic knowledge with which he was not acquainted; and that he had [...] acquired the accomplishments that form the basis of the liberal education of a gentleman, mathematics, music, knowledge of literature and poetry, and the doctrines of natural science, ethics and political science” (Cicero 1942, 99, 101, para. 127 [emphases added]). Hippias is known to have lectured also on grammar, history, archaeology, and astronomy, and to have written elegies and tragedies as well as technical works (Encyclopædia Britannica 2017). Sadly, only a few fragments remain.
Hippias’s curriculum (according to Cicero):
- Mathematics
- Music
- Literature and poetry
- Natural science
- Ethics
- Political science
Recall that, in the extract from Plato’s Protagoras quoted in Section 2.2 above, Hippias was singled out by Protagoras as one of those sophists who would teach the specialized subjects of the quadrivium (Plato 1961a, 317, para. 318d–e). Hippias’s life roughly coincided with that of Theodorus. There is no means of choosing either 5th-Century teacher over the other as the first to organize their activities quadrivium-wise. Given his attested versatility, Hippias may well have had different ideas as to the appropriate range of the sophist’s curriculum; but the record is frustratingly silent on the matter. Hippias’s curriculum (according to Plato):
- Arithmetic
- Astronomy
- Geometry
- Music
2.6 Philolaus of Croton (c. 470 – c. 385)
Philolaus was the most prominent Pythagorean of his generation (see, e.g., Huffman 2016a), and (as Cicero reports, “not improbabl[y]”) was the teacher of Archytas of Tarentum (Huffman 2016b). Kahn suggests that, “[s]ince the time of Philolaus and Archytas, the Pythagorean homeland had been established in the quadrivium” (Kahn 2001, 153). It nevertheless remains unclear how much of Archytas’s view of the classification of the sciences (see below, Section 2.7) was influenced by Philolaus’s teaching. Philolaus’s curriculum (according to Kahn):
- Arithmetic
- Geometry
- Astronomy
- Music
2.7 Archytas of Tarentum (fl. early 4th Century)
Archytas was Philolaus’s pupil (according to Cicero), and an acquaintance of Plato (see, e.g., Huffman 2016b). He was “the last prominent figure in the early Pythagorean tradition” after Pythagoras himself and Philolaus, and one of the leading mathematicians of his time (Huffman 2016b). Of Archytas’s writings, only four fragments survive. Fragment B1, the beginning of Archytas’s book on harmonics, may well be the earliest text explicitly to identify the four areas of study that would later become known as the quadrivium:
Those concerned with the sciences [μαθήματα / mathēmata] seem to me to make distinctions well and it is not at all surprising that they have correct understanding about individual things as they are. For, having made good distinctions concerning the nature of wholes they were likely also to see well how things are in their parts. Indeed concerning the speed of the stars and their risings and settings as well as concerning geometry and numbers and not least concerning music, they handed down to us a clear set of distinctions. For these sciences seem to be akin. (Archytas 2005, 105–106, fragment 1:1–7 [emphases added]).
Archytas’s curriculum:
- Stars
- Geometry
- Numbers
- Music
Tellingly, Archytas doesn’t present this classification of the sciences as his own discovery, but praises “those concerned with the sciences”; whether or not he is here referring to his fellow Pythagoreans exclusively is unclear. The comment that “these sciences seem to be akin” is the apparent target of an allusion in Plato’s Republic concerning the relationship between astronomy and music: “We may venture to suppose [...] that as the eyes are framed for astronomy so the ears are framed for the movements of harmony, and these are in some sort kindred sciences, as the Pythagoreans affirm and we admit” (Plato 1961e, 763, book VII, para. 530d [emphases added]). At last, in the context provided by Archytas, we are able to make sense of Kahn’s assertion that “[t]he medieval quadrivium is [...] authentically Pythagorean” (Kahn 2001, p. 13).
By the end of the 5th Century BCE, then, we see the emergence of a canonical classification of the (mathematical) sciences, consisting of arithmetic, geometry, astronomy, and music — sometimes presented in that order, sometimes not.
3. The Classical period (c. 400–300 BCE)
3.1 Isocrates (436–338 BCE)
The Athenian orator and rhetorician Isocrates (see, e.g., Haskins 2004) distinguished two types of arts: the useful and the pleasurable. In his discourse Panegyricus, Isocrates refers to “the arts” as a category that encompasses “both those which are useful in producing the necessities of life and those which have been devised to give us pleasure” (Isocrates 1928, 143, para. 40). Tatarkiewicz (1970, 97; see also Tatarkiewicz 1963, 232) argues that “[t]his was a natural distinction (its origins can be found in the poets Theognis [of Megara, fl. 6th Century BCE] and Simonides [of Ceos; c. 556 – c. 468 BCE], and later in Sophocles [c. 496 – c. 406 BCE]), but it was the Sophists who applied it to art”. In On Sophists, directed against his rival Isocrates, the sophist Alcidamas of Elaea (fl. 4th Century BCE) nevertheless writes in approval of the utility/pleasure distinction (Tatarkiewicz 1970, p. 104): “[Statues] are imitations of real bodies; they give joy to the beholder, but they serve no useful purpose”. And the treatise Dissoi Logoi (Opposing Arguments; a.k.a. Dialexeis), written by an anonymous author around 400 BCE, contains the statement that “poets never write their poems to propound truth but to give pleasure” (Robinson 1979, 121, part III, para. 17).
Tatarkiewicz (1963, 232) claims that “[t]his classification was successful”. Indeed, “[i]n the Hellenistic epoch, it was as widespread as it had been in the times of the Sophists”.
Isocrates’ classification of the arts:
- Useful arts
- Architecture
- etc.
- Sculpture
- Painting
- Poetry
- etc.
3.2 Plato (428/427 – 348/347 BCE)
Plato was an Athenian philosopher, the pupil of Socrates, and the teacher of Aristotle (see, e.g., Kraut 2017). He founded the Academy, the first institution of higher education in the Western world, and is best known as the author of a body of written work “of unparalleled influence” (Meinwald 2020). In Alfred North Whitehead’s famous words, “The safest general characterization of the European philosophical tradition is that it consists of a series of footnotes to Plato” (Whitehead 1929, 63).
At least five separate knowledge organization (KO) schemes have been attributed to Plato.
One is that in which philosophy is divided into three: physics, ethics, and logic [2]. Sextus Empiricus (c. 160 – c. 210), in his Against the Logicians, Book 1 (Book 7 of Against the Learned; see below), appears to have been the first to attribute such a classification to Plato:
Some [...] hold that it [i.e., philosophy] has but one part, others that it has two, and others that it has three parts; and of those who have supposed it to consist of one part, some have supposed this to be physics, others ethics, others logic; and so likewise of those who divide it into two, some have made the divisions physics and logic, others physics and ethics, others logic and ethics; while those who divide it into three parts are all agreed on the division into physics, logic, and ethics. (Sextus 1935, 3, 5, paras. 2–4 [emphases added])[T]he view of those who divide Philosophy into Physics, Ethics, and Logic is more satisfactory. Of these Plato is, virtually, the pioneer, as he discussed many problems of physics and of ethics, and not a few of logic; but those who most expressly adopt this division are Xenocrates [of Chalcedon, c. 396/395 – c. 314/313 BCE] and the Peripatetics [c. 4th Century BCE], and also the Stoics [c. 3rd Century BCE]. (Sextus 1935, 9, para. 16 [emphases added])
Regarding Philosophy then, as tripartite, some put Physics as its first division since it holds first place both in point of time — seeing that even up till now the earliest philosophers have been called ‘physicists’ — and also in natural order, as it is fitting to begin by discussing the Whole before we go on to investigate the particulars and Man himself. Others have begun with Ethics, as a more necessary subject [...]. The Epicureans [c. 3rd Century BCE] start off with Logic [...]. The Stoics themselves, too, say that Logic comes first, and Ethics second, while Physics occupies the last place. (Sextus 1935, 11, 13, paras. 20, 22 [emphases added])
Note that, strictly speaking, Sextus’s claim is that Plato merely discussed problems that might conceivably be classed in the three categories of physics, ethics, and logic; not that Plato consciously adopted this scheme for organizing his ideas about those problems (as, it is implied, Xenocrates and others did). Šamurin (1955) posits that, nevertheless, the rationale for the division into logic, physics, and ethics is in fact supplied by Plato’s own distinction in Republic (book 4, 434d–441c) between three parts of the human soul: the rational part (λογιστικόν / logistikón), the spirited part (θυμοειδές / thumoeidés), and the appetitive part (ἐπιθυμητικόν / epithumētikón).
Plato’s division of philosophy (according to Sextus):
- Physics
- Ethics
- Logic
A second KO scheme, attributed to Plato by Diogenes Laertius (fl. 3rd Century CE), is that which distinguishes between “three kinds of knowledge: practical, productive, and theoretical” (Diogenes Laertius 2018, 168, book 3, para. 84):
Architecture and shipbuilding are productive; for the work produced by them can be seen. Politics, flute playing, harp playing, and so forth are practical; for they produce nothing visible, but they perform something: in one case a man plays the flute, in another the harp, and in another he engages in politics. Geometry and harmonics and astronomy are theoretical; for they neither perform nor produce anything. But the geometer examines how lines relate to one another; the student of harmonics investigates sounds; and the astronomer studies the stars and the universe. Thus some knowledge is theoretical, some practical, and some productive. (Diogenes Laertius 2018, 169, book 3, para. 84)
Strikingly, however, this particular division is not to be found in any of Plato’s writings (Tatarkiewicz 1963, 235). We do find it, instead, in Aristotle’s (see below, Section 3.5). This is perhaps not surprising when one considers that the passage in Lives of the Eminent Philosophers from which the above quotation is taken — book 3, paras. 80–109 — is itself based upon a text attributed to Aristotle (Mutschmann 1906) [3].
Plato’s division of knowledge (according to Diogenes Laertius):
- Productive
- Architecture
- Shipbuilding
- Practical
- Politics
- Flute playing
- Harp playing
- Theoretical
- Geometry
- Harmonics
- Astronomy
Two related schemes do appear in Plato’s works. Firstly, in the Sophist (Plato 1961c, 961, paras. 219a–c), a distinction is made between productive and acquisitive art [4]:
Stranger: And of arts there are two kinds?
Theaetetus: What are they?
Stranger: There is agriculture, and the tending of mortal creatures, and the art of constructing or molding vessels, and there is the art of imitation — all these may be appropriately called by a single name.
Theaetetus: What do you mean? And what is the name?
Stranger: He who brings into existence something that did not exist before is said to be a producer, and that which is brought into existence is said to be produced.
Theaetetus: True.
Stranger: And all the arts which were just now mentioned are characterized by this power of producing?
Theaetetus: They are.
Stranger: Then let us sum them up under the name of productive or creative art.
Theaetetus: Very good.
Stranger: Next follows the whole class of learning and cognition; then comes trade, fighting, hunting. And since none of these produces anything, but is only engaged in conquering by word or deed, or in preventing others from conquering, things which exist and have been already produced — in each and all of these branches there appears to be an art which may be called acquisitive.
Theaetetus: Yes, that is the proper name.
Plato’s classification of art:
- Productive art
- Agriculture
- Medicine
- Shipbuilding
- Painting and sculpture
- Acquisitive art
- Learning and cognition
- Trade
- Fighting
- Hunting
- Fishing
Secondly, in the Statesman (Plato 1961d–e, 1048, paras. 281d), a distinction is made between productive and contributory arts:
Stranger: To begin with, let us observe that two groups of arts are involved in active operations of all kinds.
Young Socrates: What are they?
Stranger: One class contributory to the production, the other actually producing.
Young Socrates: In what way?
Stranger: I mean by ‘contributory’ arts those which do not fashion the product itself but prepare the tools for the arts which actually produce it — they are arts without whose previous assistance the specific task of the productive arts could never be performed. The arts which fashion the product itself are the ‘productive’ arts, strictly speaking.
Young Socrates: That is at any rate a reasonable distinction.
Stranger: Then may we take the further step of distinguishing arts which manufacture spindles, shuttles, and all the other instruments of clothes manufacture as ‘contributory arts’ from the directly ‘productive’ arts which actually treat and produce the clothes?
Young Socrates: We certainly may.
Plato’s classification of arts:
- Productive arts
- Contributory arts
- “arts which make instruments, containers, carriages, ‘defenses’ (including weaving, clothing, armor, walls, stonework and others), diversions (visual arts, poetry, music), nourishments (farming, hunting, gymnastics, medicine, butchering) as well as those handling raw material such as mining, lumbering, the currier’s art, the art of stripping bark and the arts of making cork, papyrus and rope” (Whitney 1990, 33)
A fifth KO scheme which (unlike the first two) has been securely attributed to Plato is derived from a standard reading of the Republic, Books 2, 3, and 7, in which education (παιδεία / paideía) is divided into music (including literature), gymnastics, arithmetic, (plane) geometry, stereometry (i.e., solid geometry), astronomy, harmonics, and dialectic [5].
What, then, is our education? Or is it hard to find a better than that which long time has discovered — which is, I suppose, gymnastics for the body, and for the soul, music? [...] And shall we not begin education in music earlier than in gymnastics? [...] And under music you include tales, do you not? [...] And tales are of two species, the one true and the other false? Yes. (Plato 1961e, 623, book II, para. 376e [emphases added]).
[E]ducation in music is most sovereign, because more than anything else rhythm and harmony find their way to the inmost soul and take strongest hold upon it, bringing with them and imparting grace (Plato 1961e, 646, book III, para. 401d [emphasis added]). After music our youth are to be educated by gymnastics? Certainly (Plato 1961e, 648, book III, para. 403c [emphasis added]).
[I]n our previous account they [i.e., youth] were educated in gymnastics and music (Plato 1961e, 754, book VII, para. 521e). [A]mong the first things that everybody must learn [... are] number and calculation. Is it not true of them that every art and science must necessarily partake of them? (522c). [T]he study that comes next is [...] geometry (526c). [G]eometry is the knowledge of the eternally existent (527b). Shall we set down astronomy as a third [...]? (527d). [W]e just now did not rightly select the study that comes next after geometry [...]. The right way is next in order after the second dimension to take the third. This, I suppose, is the dimension of cubes and of everything that has depth (528a–b). We may venture to suppose [...] that as the eyes are framed for astronomy so the ears are framed for the movements of harmony, and these are in some sort kindred sciences, as the Pythagoreans affirm and we admit (530d). [A]ll this is but the preamble of the law itself [...] the very law which dialectic recites (531d–532a) [Emphasis added].
Through the voice of Socrates (c. 470 – 399 BCE), Plato is here explaining an ideal system of higher education in which youths who have excelled in music and gymnastics spend ten years in the study of five mathēmata: number and calculation (i.e., arithmetic); plane geometry; solid geometry; astronomy; and harmonics. These ten years are to be followed by five of dialectic, and fifteen gaining practical political and military experience, before the students may “alternate between pursuing philosophy and applying their knowledge of the Good to ruling their city state” (Mueller 1991, 85). This is the form of higher education that Socrates deems requisite for producing “maximally fair and knowledgeable” rulers (Mueller 1991, 85), and the passage in which Plato describes it has had “a decisive and long-lasting impact” on the history of education (Mueller 1991, 86). In particular, the five mathēmata — reducible to four once the two forms of geometry are combined — are immediately recognizable as constituting the quadrivium. Indeed, the Greek word mathēmata is “simply the plural of a word which might be translated ‘discipline’ or ‘subject of study’” (Mueller 1991, 85).
Socrates’ curriculum (according to Plato):
- Youth
- Music
- Gymnastics
- Next 10 Years
- Arithmetic
- Geometry
- Stereometry
- Astronomy
- Harmonics
- Next 5 Years
- Dialectic
- Next 15 Years
- practical political and military experience
- Rest of Life
- Philosophy
- ruling
Plato does not represent Socrates as the first to recommend the subjects of the quadrivium. As we have seen, both Theodorus of Cyrene (see above, Section 2.4) and Hippias of Elis (see above, Section 2.5) are identified by Plato (in the Theaetetus and the Protagoras, respectively) as knowledgeable teachers in precisely these areas.
3.3 Speusippus of Athens (c. 408 – 339/338 BCE)
Speusippus was Plato’s nephew, i.e., Plato’s sister Potone’s son (see, e.g., Guthrie 1978, 457–469; Tarán 1981; Dillon 1996, 11–22). He succeeded Plato as head of the Academy in 348 BCE. Diogenes Laertius (fl. 3rd Century) says that “Speusippus was the first, according to Diodorus [Cronus, died c. 284 BCE] in the first book of his Reminiscences, to discern the common element in studies and to relate them to one another as far as that was possible” (Diogenes Laertius 2018, 178, book 4, para. 2). James Miller, the editor of the 2018 edition of Diogenes Laertius’ Lives, adds a footnote: “An ambitious project, but no evidence survives of its contents” (Diogenes Laertius 2018, 178, book 4, fn. 6). Ernest Cushing Richardson (1930, 51) remarks that “if this be true”, Speusippus was “therefore [...] the father of scientific classification”. Speusippus was indeed responsible for various applications of the method of διαίρεσις / diaíresis (Latin divisio; division) in the production of taxonomies. Diaíresis had been introduced by Plato, and would be further developed by Aristotle: Richardson’s claim for Speusippus thus seems somewhat overblown.
3.4 Xenocrates of Chalcedon (c. 396/395 – 314/313 BCE)
Recall Sextus’s commentary on Plato’s supposed partitioning of the discipline of philosophy: “[T]he view of those who divide Philosophy into Physics, Ethics, and Logic is more satisfactory [...]. [T]hose who most expressly adopt this division [include] Xenocrates” (Sextus 1935, 9, para. 16). Xenocrates was a student of Plato, and succeeded Speusippus as head of the Academy in 339/338 BCE (see, e.g., Guthrie 1978, 469–483; Dillon 1996, 22–38; Dancy 2017). As Academy head, Xenocrates “appears to have set himself to systematize as far as possible what he understood to be the philosophical system of Plato, partly, no doubt, in response to the shrewdly aimed criticisms levelled from the Lyceum” (Dillon 1996, 23). His tripartite division of philosophy duly “became the norm” in Stoicism (see below, Section 4.2) and Hellenistic philosophy in general (Dancy 2017).
Xenocrates’ division of philosophy (according to Sextus):
- Physics
- Ethics
- Logic
3.5 Aristotle (384–322 BCE)
Aristotle, student of Plato, founder of the Lyceum and the Peripatetic school of philosophy, and teacher of Alexander the Great (356–323 BCE), is “one of the greatest intellectual figures of Western history” (Amadio and Kenny 2020). Only around a third of Aristotle’s original written work has survived; but this work has “shaped centuries of philosophy” (Shields 2015).
Aristotle is responsible for at least three KO schemes, each of great interest and influence: a classification of the sciences, a classification of the arts, and a classification of the kinds of propositions and problems used in dialectical arguments.
Aristotle refers to the various branches of knowledge (ἐπιστήμη / epistḗmē) as “sciences” (ἐπιστήμαι / epistḗmai). Among the sciences, he distinguishes between those that are theoretical (a.k.a. speculative; θεωρητική / theorētikḗ), those that are practical (πρᾱκτῐκή / prāktikḗ), and those that are productive (a.k.a. creative or poietic; ποιητική / poiētikḗ). Theoretical sciences seek knowledge for its own sake; practical sciences focus on evaluating the goodness of human activity; and productive sciences aim at the creation of beautiful or useful objects. The basis of this division was Aristotle’s classification of human knowledge into “the fundamental categories of thinking, doing and making” (Whitney 1990, 33).
Topics, Book 6: “[Knowledge] is classed as speculative, practical, and productive” (Aristotle 1984a, 244, book 6, 145a15–16 [emphases added]).
Topics, Book 8: “the distinction of sciences into speculative, practical, and productive” (Aristotle 1984a, 264, book 8, 157a9–10 [emphases added]).
Theoretical sciences include mathematics, physics or natural science, and “first philosophy” or theology (what we would now call metaphysics):
Metaphysics, Book 6: “There must, then, be three theoretical philosophies: mathematics, natural science, and theology” (Aristotle 1984b, 1620, book 6, 1026a18–19 [emphases added]).
Metaphysics, Book 11: “Evidently, then, there are three kinds of theoretical sciences — natural science, mathematics, theology” (Aristotle 1984b, 1681, book 11, 1064b1–2 [emphases added]).
Natural science includes astronomy, botany, biology, and possibly what we would now call psychology. Aristotle’s works that are most relevant to the theoretical sciences include the Physics, Metaphysics, De Anima (On the Soul), and De Caelo (On the Heavens). Practical sciences include politics and ethics. Relevant works include the Nicomachean Ethics and Eudemian Ethics. Productive sciences include the arts (music, theater, dance), rhetoric (“which treats the principles of speech-making appropriate to various forensic and persuasive settings”; Shields 2015), medicine, agriculture, and shipbuilding. Relevant works include the Poetics and Rhetoric.
Aristotle’s classification of the sciences:
- Theoretical
- Mathematics
- Natural science
- Astronomy
- Botany
- Biology
- Theology
- Practical
- Politics
- Ethics
- Productive
- the Arts
- Rhetoric
- Medicine
- Agriculture
- Shipbuilding
On the face of it, Aristotle’s classification of the sciences is reminiscent of the division of knowledge attributed to Plato by Diogenes Laertius (see above, Section 3.2). The top-level categories are the same in each case. Whitney (1990, 34) claims that “in all likelihood” Aristotle borrowed the term “productive” (ποιητική) from Plato. A closer look, however, reveals significant differences. For example, Plato’s scheme locates music under theoretical and practical knowledge, while for Aristotle music is classified as one of the arts, under the productive sciences.
Logic remains outside Aristotle’s scheme. Aristotle’s work on logic makes up part of the group of works known as the Organon, which means “tool” in Greek. This reflects the idea of logic as a tool that is used in the same way in all sciences, whether theoretical, practical, or productive. Works in the Organon include the Categories, De Interpretatione, Prior Analytics, Posterior Analytics, and Topics.
Tatarkiewicz (1963, 233) claims that, “[f]rom the point of view of aesthetics, [Aristotle’s] was certainly the most important of all the classifications of arts attempted in ancient times”. Tatarkiewicz finds evidence of this classification in a single statement in Physics, book 2, 199a15 (Aristotle 1984a, 340 [emphases added]): “generally art in some cases completes what nature cannot bring to a finish, and in others imitates nature”.
Aristotle’s classification of the arts:
- Arts that complete nature
- Arts that imitate nature
- Painting
- Sculpture
- Poetry
Turning to Aristotle’s classification of propositions and problems, we again find an outline presented in the Topics:
Topics, Book 1: “Of propositions and problems there are — to comprehend the matter in outline — three divisions; for some are ethical propositions, some are on natural science, while some are logical” (Aristotle 1984a, 175–176, book 1, 105b19–21 [emphases added]).
Aristotle’s classification of propositions and problems:
- Ethical
- Natural science
- Logical
The similarity of this scheme to Xenocrates’ division of philosophy is noted both by Guthrie (1978, 478) and by Dillon (1996, 23). Does Aristotle’s scheme reflect influence from the Academy? Or did the influence flow in the other direction? The currently available evidence cannot resolve this particular problem. Suffice to say that the tripartite Physics–Ethics–Logic division was very much “in the air” in 4th-Century Athens [6].
4. The Hellenistic period (c. 300–150 BCE)
4.1 Epicurus (341–270 BCE)
Born on the island of Samos, Epicurus founded several philosophical schools during his lifetime; after his death, Epicureanism continued to flourish as a movement for hundreds of years (see, e.g., Konstan 2018). Epicurus taught that philosophy is “a way of life, not a mere intellectual pastime” (Shaw 2020, 14): an “utterly practical” system dedicated to curing the soul and thereby bringing about the good life (Shaw 2020, 13).
Given this instrumental conception of philosophy, Epicureans tend to reject logic, mathematics, rhetoric, and literary theory as useless (Shaw 2020, 15). Epicurus “divided philosophy into three parts — canonic, physics, and ethics” (Diogenes Laertius 2018, 504, book 10, para. 29 [emphases added]). The canonic part is “the science that concerns criteria and first principles, or the fundamentals of philosophy”; the physical part “deals with becoming, perishing, and nature”; and the ethical part “deals with things to be chosen and avoided, and with ways of life and the end” (Diogenes Laertius 2018, 504, book 10, para. 30).
Epicurus’s division of philosophy (according to Diogenes Laertius):
- Canonic
- Physics
- Ethics
4.2 Zeno of Citium (c. 334 – c. 262 BCE)
Zeno of Citium was the founder of the Stoic school of philosophy (see, e.g., Baltzly 2018). He is not to be confused with Zeno of Elea (c. 495 – c. 430 BCE), Zeno of Tarsus (fl. 200 BCE), or Zeno of Sidon (c. 150 – c. 75 BCE). Diogenes Laertius (fl. 3rd Century) says Zeno of Citium was the first to divide philosophy up into logic, physics, and ethics:
They [i.e., the Stoics] say that philosophical doctrine has three parts: the physical, the ethical, and the logical. Zeno of Citium was the first to divide it this way in his work On Reason. (Diogenes Laertius 2018, 328, book 7, para. 39 [emphases added])
No part is separate from another, as some of the Stoics say; instead, the parts are blended together. And they used to teach them in combination. Others present logic first, physics second, and ethics third. Among these are Zeno in his work On Reason. (Diogenes Laertius 2018, 329, book 7, para. 40 [emphases added])
Unfortunately, Zeno’s work On Reason has not survived.
Zeno’s division of philosophy (according to Diogenes Laertius):
- Logic
- Physics
- Ethics
4.3 Cleanthes of Assos (c. 330 – c. 230 BC)
Cleanthes was Zeno’s successor as head of the Stoa (see, e.g., Baltzly 2018). Diogenes Laertius records that, according to Cleanthes, “there are six parts [of philosophical doctrine/discourse]: dialectic, rhetoric, ethics, politics, physics, and theology” (Diogenes Laertius 2018, 329, book 7, para. 41 [emphases added]). Dialectic and rhetoric together comprise logic: “Some say that the logical part is divided into two branches: rhetoric and dialectic [...]. Rhetoric they regard as a knowledge of how to speak well in an expository manner, and dialectic as the knowledge of how to discourse correctly in speeches conducted by question and answer; hence they define it as the science of the true, the false, and that which is neither true nor false” (Diogenes Laertius 2018, 329, book 7, para. 41–42).
It is easy to see how Cleanthes’ scheme is an expanded version of Zeno’s tripartite classification, presented in the same basic sequence. Cleanthes’ dialectic and rhetoric are equivalent to Zeno’s logic; Cleanthes’ ethics and politics are equivalent to Zeno’s ethics; and Cleanthes’ physics and theology are equivalent to Zeno’s physics (since, for the Stoics, Nature and God were equivalent terms; Long 1986, 108). Cleanthes’ division of philosophy (according to Diogenes Laertius):
- Dialectic
- Rhetoric
- Ethics
- Politics
- Physics
- Theology
4.4 Callimachus of Cyrene (c. 305 – c. 240 BCE)
Born in what is now Libya, Callimachus was a 3rd-Century BCE Greek poet and scholar who worked for King Ptolemy II Philadelphus (308–246 BCE) at the Library of Alexandria in Egypt (see, e.g., Acosta-Hughes, Lehnus and Stephens 2011). Callimachus compiled the Pínakes (Tablets) in 120 volumes, a vast biographical catalog of the authors of works held in the Library, of which only a few fragments survive (Witty 1958). Francis J. Witty presents these fragments in English translation, “collected under the classes [...] in which Callimachus probably first included them” (Witty 1958, 132). These eight classes are as follows [7]: Oratory; History; Laws; Philosophy; Miscellany; Medicine; Lyric poetry; and Tragedy.
Callimachus’s library classification:
- Oratory
- History
- Laws
- Philosophy
- Miscellany
- Medicine
- Lyric poetry
- Tragedy
4.5 Chrysippus of Soli (c. 279 – c. 206 BCE)
Chrysippus was Cleanthes’ successor (see, e.g., Baltzly 2018). Just as Zeno of Citium divided philosophy into the logical, the physical, and the ethical, reports Diogenes Laertius (2018, 328, book 7, para. 39), “Chrysippus did the same in the first book of his work On Reason and in the first book of his Physics”. Neither of these works has survived.
There is some controversy, however, over Chrysippus’s sequencing of the three parts (Long 1986, 120). Plutarch (1874, 432 [emphases added]) records in De Stoicorum repugnantiis (1035a) that “Chrysippus is of opinion, that young students should first learn logic, secondly, ethics, and after these, physics”.
Chrysippus’s division of philosophy (according to Plutarch):
- Logic
- Ethics
- Physics
5. The Roman period (c. 150 BCE – 250 CE)
5.1 Dionysius Thrax (c. 170 – c. 90 BCE)
Dionysius, who was called Thrax because his father was from Thrace, is traditionally credited as the author of a short grammar of classical Greek, the Tékhnē grammatikē (Art of Grammar), long thought to be “the first grammar of any language to be written in the western world” (Robins 1957, 67). An absence of citations to the main body of the work before the 5th Century CE, however, has provoked modern skepticism that it can be dated to Dionysius’s time (see, e.g., Law 1990, 89).
Immanuel Bekker’s publication in 1816 of the 15-page Greek text of the Tékhnē grammatikē together with 325 pages of accompanying scholia (i.e., commentaries) attracted attention not only to the former but also to the latter. There we find the claim that Dionysius divided arts into four: theoretical, practical, apotelesmatic, and peripoietic (Bekker 1816, 670; see also Tatarkiewicz 1963, 235–236). Tatarkiewicz (1963, 235) glosses “apotelestic” (his spelling of “apotelesmatic”) as “finished”, “carried out to its end”, and equates the category to Quintilian’s poietic or productive arts (see below, Section 5.8). By “peripoietic” (explains Tatarkiewicz, 1963, 236), Dionysius meant “the group of arts, already noticed by Plato, that simply make use of nature, like fishing or hunting, without producing anything new”.
Dionysius’s first classification of the arts (according to Dionysian scholia):
- Theoretical
- Astronomy
- Philosophy
- Practical
- Zither playing
- Dancing
- Apotelesmatic
- Statuary
- Building
- Peripoietic
- Hunting
- Fishing
Earlier in the same scholium, a separate classification divides arts into a different set of four groups: productive, theoretical, practical, and mixed (Bekker 1816, 652; see also Whitney 1990, 37). “Productive arts are those which fashion ‘a certain matter which has been wrought’ into an artificial thing [...]. Practical arts are arts executed by means of instruments [...]. Theoretical arts are the familiar category [...]. Finally, ‘mixed’ arts are those which seem to combine the other categories” (Whitney 1990, 37).
Dionysius’s second classification of the arts (according to Dionysian scholia):
- Productive
- Metal-working
- Shoemaking
- Carpentry
- Practical
- Military art
- Theoretical
- Astronomy
- Philosophy
- Mixed
- Medicine
Also appearing in the scholia to the Tékhnē grammatikē is a combination of the two other schemes. This is attributed to the grammarian Lucius Tarrhaeus, about whom little else is known, but who is said to have divided arts into apotelesmatic, practical, organic (or instrumental), and theoretical (Bekker 1816, 652–654; see also Tatarkiewicz 1963, 236; Whitney 1990, 37). Here, apotelesmatic arts are described as arts using one or more materials; practical arts are arts using actions; organic arts are those involving the playing of musical instruments; theoretical arts include astronomy and geometry.
Lucius Tarrhaeus’s classification of the arts (according to Dionysian scholia):
- Apotelesmatic
- Carpentry
- Metalworking
- Architecture
- Practical
- Dancing
- Wrestling
- Javelin throwing
- Oratory
- Hunting
- Fishing
- Driving horses
- Steering ships
- Organic
- Flute playing
- Theoretical
- Astronomy
- Geometry
5.2 Posidonius of Apamea (c. 135 – c. 51 BCE)
Posidonius, pupil of the Stoic philosopher Panaetius (c. 180 – 109 BCE), was a historian and polymath, renowned as the most learned man of his age (see, e.g., Kidd 1988).
In the present context, Posidonius interests us in two ways. Firstly, he is known for his adherence to the characteristic Stoic classification of the parts of philosophy. Recall Diogenes Laertius’s summary of this division: “philosophical doctrine has three parts: the physical, the ethical, and the logical”. While Zeno of Citium was “the first to divide it this way”, Diogenes Laertius confirms that Posidonius “did the same” (Diogenes Laertius 2018, 328, book 7, para. 39), and goes on to claim that “Posidonius begin[s] with physics, as Phanias, a student of Posidonius, says in the first book of his work Lectures of Posidonius” (Diogenes Laertius 2018, 329, book 7, para. 41). Posidonius’s division of philosophy (according to Diogenes Laertius):
- Physics
- Ethics
- Logic
At the same time, Posidonius is also remembered for his classification of the arts, knowledge of which we have from the Epistulae Morales ad Lucilium (a.k.a. Letters from a Stoic) of the Hispano-Roman philosopher and statesman Lucius Annaeus Seneca (c. 4 BCE – 65 CE): “Posidonius divides the arts into four classes: first we have those which are common and low [or vulgar and degrading], then those which serve for amusement [or entertainment], then those which refer to the education [or instruction] of boys, and, finally, the liberal arts”. The common arts, which “belong to workmen and are mere hand-work [...] are concerned with equipping life”. The arts of amusement are “those which aim to please the eye and the ear”. The concern of the liberal arts — or, “to give them a truer name”, the “free” arts — is “virtue” (Seneca 1920, 363, no. 88, paras. 21–23 [emphases added]).
Posidonius’s classification of the arts (according to Seneca):
- Common arts
- Arts of amusement
- Educational arts
- Liberal arts
5.3 Geminus (fl. 1st Century BCE)
Geminus was a Greek astronomer and mathematician, possibly from Rhodes, who may have been a pupil of Posidonius (see, e.g., Evans and Berggren 2007). His work on mathematics has not survived, and our knowledge of it is due to commentators such as the Neoplatonist Proclus (412–485), who was “the most authoritative philosopher of late antiquity” (Helmig and Steel 2020).
In his Commentary on the First Book of Euclid’s Elements, Proclus outlines Geminus’s division of the parts of mathematics: “[O]thers, like Geminus, think that mathematics should be divided differently; they think of one part as concerned with intelligibles only and of another as working with perceptibles and in contact with them. By intelligibles, of course, they mean those objects that the soul arouses by herself and contemplates in separation from embodied forms. Of the mathematics that deals with intelligibles they posit arithmetic and geometry as the two primary and most authentic parts, while the mathematics that attends to sensibles contains six sciences: mechanics, astronomy, optics, geodesy, canonics, and calculation [...]. These, then, are the species of general mathematics. Geometry in its turn is divided into plane geometry and stereometry [...]. In the same way arithmetic is divided into the study of linear numbers, plane numbers, and solid numbers” (Proclus 1970, 31–32, chap. XIII, paras. 38–39 [emphases added]; see also Mueller 2004, 76–82).
Geminus’s division of mathematics (according to Proclus):
- Mathematics of intelligibles
- Arithmetic
- Linear numbers
- Plane numbers
- Solid numbers
- Geometry
- Plane geometry
- Stereometry
- Arithmetic
- Mathematics of perceptibles
- Mechanics
- Astronomy
- Optics
- Geodesy
- Canonics
- Calculation
5.4 Marcus Terentius Varro (116–27 BCE)
Varro was a polymathic Roman scholar of the 1st Century BCE (see, e.g., Taylor 1974). According to Friedrich Ritschl, Varro’s work Disciplinarum libris IX (Nine Books of Disciplines), now lost, consisted of the following books: I de grammatica; II de dialectica; III de rhetorica; IV de geometria; V de arithmetica; VI de astrologia; VII de musica; VIII de medicina; IX de architectura (Ritschl 1877, 371). The nine disciplines thus comprise grammar, dialectic, rhetoric, geometry, arithmetic, astrology, music, medicine, and architecture, and Varro’s work appears to be “the earliest Latin classification and exposition of the liberal arts” (Weisheipl 1985, 204) [8].
Varro’s curriculum (according to Ritschl):
- Grammar
- Dialectic
- Rhetoric
- Geometry
- Arithmetic
- Astrology
- Music
- Medicine
- Architecture
Doody (2009, 6) casts doubt on Ritschl’s reconstruction: “From the scattered references and the title, it seems that [Disciplinarum libris IX] is a book that dealt with a number of arts or disciplines, but it is not possible to know exactly which and how many disciplines were discussed, or the manner in which they were addressed”. If we nevertheless accept Ritschl’s analysis, two remarkable aspects of Varro’s curriculum emerge:
- It encapsulates the distinction between (what would later come to be known as) the trivium of grammar, dialectic, and rhetoric, and (what would later come to be known as) the quadrivium of geometry, arithmetic, astrology (a.k.a. astronomy), and music.
- It also encapsulates the distinction between the liberal arts (see Section 5.5 on Cicero, below), and two important productive or “vulgar” arts, viz. medicine and architecture.
Both of these distinctions were to become especially salient in Western medieval culture.
5.5 Marcus Tullius Cicero (106–43 BCE)
Cicero was a Roman statesman, orator, and writer (see, e.g., Powell 1995). He was the first to use the Latin term artēs liberales (“liberal arts”), in his De oratore (Wolfe 1995). As we saw above (under Hippias, Section 2.5), the liberal arts were deemed by Cicero to include mathematics, music, literature and poetry, natural science, ethics, and political science (Cicero 1942, 99, 101, para. 127). All of these were considered to be based primarily on the application of thinking skills, in contrast to the practical arts (e.g., medicine and architecture). An education in the liberal arts was seen as the appropriate foundation for the “higher learning” of philosophy and theology.
Cicero’s curriculum:
- Mathematics
- Music
- Literature and poetry
- Natural science
- Ethics
- Political science
Cicero used or invented several other classifications of the arts. One involved the Isocratic distinction between “arts cultivated for the sake of utility, and [...] arts cultivated for the sake of amusement” (Tatarkiewicz 1963, 236). Another was based on a division by importance, distinguishing major, mean, and minor arts (artēs maximae, mediocres, and minores). “To the major arts belonged [...] political and warlike arts; to the second class, purely intellectual arts, i.e. sciences, but also poetry and eloquence; to the third class, all the other arts: painting, sculpture, music, acting, athletics” (Tatarkiewicz 1963, 236) [9]. Comparison of Cicero’s major and mean classes of arts with the Aristotelean practical and theoretical classes of sciences indicates a reversal in the valuation of politics, on the one hand, and natural science, on the other.
Cicero’s first classification of the arts (according to Tatarkiewicz):
- Major arts
- Political arts
- Warlike arts
- Mean arts
- Sciences
- Poetry
- Eloquence
- Minor arts
- Painting
- Sculpture
- Music
- Acting
- Athletics
In De officiis (On Duties), Cicero classifies occupations, distinguishing those that are vulgar (sordidi) from those that are liberales:
Now in regard to trades and other means of livelihood, which ones are to be considered becoming to a gentleman and which ones are vulgar, we have been taught, in general, as follows. First, those means of livelihood are rejected as undesirable which incur people’s ill-will, as those of tax-gatherers and usurers. Unbecoming to a gentleman, too, and vulgar are the means of livelihood of all hired workmen whom we pay for mere manual labour, not for artistic skill; for in their case the very wage they received is a pledge of their slavery. Vulgar we must consider those also who buy from wholesale merchants to retail immediately; for they would get no profits without a great deal of downright lying; and verily, there is no action that is meaner than misrepresentation. And all mechanics are engaged in vulgar trades; for no workshop can have anything liberal about it. Least respectable of all are those trades which cater for sensual pleasures: ‘Fishmongers, butchers, cooks, and poulterers, and fishermen’, as Terence says. Add to these, if you please, the perfumers, dancers, and the whole corps de ballet.
But the professions in which either a higher degree of intelligence is required or from which no small benefit to society is derived — medicine and architecture, for example, and teaching — these are proper for those whose social position they become. Trade, if it is on a small scale, is to be considered vulgar; but if wholesale and on a large scale [...] it is not to be greatly disparaged [...]. But of all the occupations by which gain is secured, none is better than agriculture, none more profitable, none more delightful, none more becoming to a freeman. (Cicero 1913, 153, 155, book 1, section 42, paras. 150–151 [emphases added])
Cicero’s classification of occupations:
- Vulgar trades
- Tax-gathering
- Usury
- Waged manual labor
- Retail trade
- Mechanics
- Fishmongery
- Butchery
- Cookery
- Poultery
- Fishing
- Perfumery
- Dancing
- Liberal trades
- Medicine
- Architecture
- Teaching
- Wholesale trade
- Agriculture
One further classification of the arts is “just mentioned incidentally in [Cicero’s] writings” (Tatarkiewicz 1963, 236; cf. Cicero 1942, 23, book 3, section 7, para. 26): this one distinguishes the arts of language (i.e., poetry and oratory) and the silent arts (artēs mutae; i.e., painting and sculpture).
Cicero’s second classification of the arts:
- Arts of language
- Poetry
- Oratory
- Silent arts
- Painting
- Sculpture
5.6 Philo of Alexandria (c. 15 BCE – 45 CE)
Philo was a Hellenistic Jewish philosopher who lived in the Roman province of Egypt in the early part of the 1st Century CE (see, e.g., Alesse 2008). His work of present relevance is De congressu quaerendae eruditionis gratia (On Mating with the Preliminary Studies) [10]: nowhere else “do we find so full a treatment of the Stoic doctrine, that the accepted school course or Encyclia was the proper preparation for philosophy” (Colson and Whitaker 1932, 452). The preliminary studies (enkýklios paideía, in other words), are the handmaid — “the lower instruction given by the lower branches of school lore” (Philo 1932, 465, para. 14) — to philosophy.
For grammar teaches us to study literature in the poets and historians, and will thus produce intelligence and wealth of knowledge. It will teach us also to despise the vain delusions of our empty imagination by shewing us the calamities which heroes and demi-gods who are celebrated in such literature are said to have undergone. Music will charm away the unrhythmic by its rhythm, the inharmonious by its harmony, the unmelodious and tuneless by its melody, and thus reduce discord to concord. Geometry will sow in the soul that loves to learn the seeds of equality and proportion, and by the charm of its logical continuity will raise from those seeds a zeal for justice. Rhetoric, sharpening the mind to the observation of facts, and training and welding thought to expression, will make the man a true master of words and thoughts, thus taking into its charge the peculiar and special gift which nature has not bestowed on any other living creature. Dialectic, the sister and twin, as some have said, of Rhetoric, distinguishes true argument from false, and convicts the plausibilities of sophistry, and thus will heal that great plague of the soul, deceit. (Philo 1932, 465, 467, paras. 15–18 [emphases added]) [11]
Philo’s curriculum:
- Grammar
- Music
- Geometry
- Rhetoric
- Dialectic
5.7 Gaius Plinius Secundus (23/24 – 79)
Pliny the Elder was a Roman military officer and natural philosopher of the 1st Century CE (see, e.g., Gibson and Morello 2011). He was author of the encyclopedic, 37-book Naturalis Historia (Natural History), completed around 77 CE (Doody 2010) [12]. The books are organized by topic as follows (Stannard 2020):
Book I: a summary of II–XXXVII
Book II: cosmology and astronomy
Books III–VI: the physical and historical geography of the ancient world
Books VII–XI: zoology: humans (VII), mammals and reptiles (VIII), fishes and other marine animals (IX), birds (X), and insects (XI)
Books XII–XIX: botany, including agriculture (XVIII)
Books XX–XXXII: medicine and drugs
Books XXXIII–XXXVII: minerals, precious stones, metals, and their uses in art and architecture
Pliny’s organizing principle seems to be one of decreasing levels of complexity — from stars and planets, to the Earth and human beings, to animals and plants, to organic and inorganic chemistry. This may be viewed as a historical precursor to (what will later be known as) scala naturae, the ladder of nature, a.k.a. → the Great Chain of Being (see, e.g., Kleineberg 2017).
Pliny’s encyclopedic classification:
- Cosmology and astronomy
- Physical and historical geography
- Zoology
- Botany
- Agriculture
- Medicine
- Minerals and art and architecture
5.8 Marcus Fabius Quintilianus (c. 35 – c. 100)
Quintilian was a Roman rhetorician of the 1st Century CE (see, e.g., Kennedy 1962). In his Institutio oratoria (Institutes of Oratory), published around 95 CE, he divided the arts into three groups: theoretical, practical, and productive (Tatarkiewicz 1963, 234):
But as some arts consist merely in an insight into things, that is, knowledge of them, and judgment concerning them, such as astronomy, which requires no act, but is confined to a mere understanding of the matters that form the subject of it (a sort of art which is called theoretic); others in action, the object of which lies in the act, and is fulfilled in it, leaving nothing produced from it (a sort of art which is called practic), as dancing; others in production, which attain their end in the execution of the work which is submitted to the eye (a sort which we call productive), as painting, we may pretty safely determine that oratory consists in act, for it accomplishes in the act all that it has to do. Such indeed has been the judgment pronounced upon it by every one”. (Watson 1891, 159–160, book II, chap. XVIII, paras. 1–2 [bold emphases added])
The distinction between theoretical, practical, and productive arts bears clear echoes of (A) the distinction between theoretical, practical, and productive knowledge attributed to Plato by Diogenes Laertius (but not expressed in any of Plato’s writings; see above, Section 3.2), and (B) the distinction between theoretical, practical, and productive sciences maintained by Aristotle and explicitly presented in several of his works (see above, Section 3.5).
Quintilian’s classification of the arts:
- Theoretic
- Astronomy
- Practic
- Dancing
- Oratory
- Productive
- Painting
5.9 Plutarch (c. 46 – c. 120)
The Platonist philosopher and biographer Plutarch, of Chaeronea in Boeotia, is best known for his Bioi parallēloi (Parallel Lives) and Moralia (Ethical Essays; see, e.g., Karamanolis 2014).
Tatarkiewicz (1963, 232) states, without citation, that Isocrates’ classification of the arts “reappeared in a more developed form in Plutarch”. Tatarkiewicz continues (bold emphases added): “To the arts necessary in life and those which serve pleasure, [Plutarch] added a third category: the arts cultivated for the sake of perfection [...]. Among the arts cultivated for the sake of perfection he does not mention sculpture or music, but quite different human works: sciences, mathematics, and astronomy”. From this brief outline, we may derive the schema depicted below:
- Useful arts
- Pleasurable arts
- Arts cultivated for the sake of perfection
- Sciences
- Mathematics
- Astronomy
5.10 Theon of Smyrna (fl. c. 100)
Theon was a Greek mathematician and philosopher in the late 1st and early 2nd Centuries CE (see, e.g., Petrucci 2017). He wrote Expositio rerum mathematicarum ad legendum Platonem utilium (On Mathematics Useful for the Understanding of Plato), which consisted of two books: the first divided into two parts, covering number and music respectively; and the second covering astronomy. Theon’s organizing principle may therefore be interpreted as a tripartite classification of mathematics:
- Number
- Music
- Astronomy
5.11 Nicomachus of Gerasa (fl. c. 150)
Nicomachus was a mathematician and “avowed Pythagorean” from Roman Syria who wrote Arithmētikē eisagōgē (Introduction to Arithmetic) (Kahn 2001, 153). According to Tarán (1969, 5), this work, “despite its poorness from a mathematical point of view, was the most influential work on arithmetic from the time it was written [...] until the sixteenth century”. It was translated into Latin by Apuleius (c. 124 – c. 170) and by Boethius (c. 477 – 524), and is “the ultimate source” of the arithmetical treatises of Capella (fl. c. 410 – 420), Cassiodorus (490 – c. 585), and Isidore (c. 560 – 636).
In his Introduction, Nicomachus posits a structure of four mathematical sciences called τέσσαρες μέθοδοι (téssares méthodoi; the “four methods”; cf. Nicomachus 1926, 187). Two of these sciences deal with quantity — arithmetic and music — and two with size — geometry and astronomy:
Things [...] are some of them unified and continuous [...] which are properly [...] called ‘magnitudes’; others are discontinuous [...] which are called ‘multitudes’ [...]. Wisdom, then, must be considered to be the knowledge of these two forms. Since, however, all multitude and magnitude are by their own nature of necessity infinite [...] and since sciences are always sciences of limited things [...] a science [...] would arise to deal [...] with quantity, set off from multitude, and size, set off from magnitude [...]. [I]t is clear that two scientific methods will [...] deal with the whole investigation of quantity; arithmetic, absolute quantity, and music, relative quantity. And [...] two other sciences in the same way will accurately treat of ‘size,’ geometry the part that abides and is at rest, astronomy that which moves and revolves. (Nicomachus 1926, 183–184 [emphases added])
Nicomachus’s division of mathematics:
- Arithmetic
- absolute quantity
- Music
- relative quantity
- Geometry
- size at rest
- Astronomy
- size in motion
5.12 Galen (129 – c. 216)
Born in Pergamon, Anatolia, Galen was a Greek physician and philosopher who “exercised a dominant influence on medical theory and practice in Europe from the Middle Ages until the mid-17th century” (Nutton 2020).
At the close of his Protrepticus (Exhortation to Study the Arts), Galen (1997, 52 [emphases added]) distinguishes high (liberal) and low (manual) arts: “[T]here is a basic distinction in kinds of Art: there are the high arts, which are associated with reason, and there are the less-respected arts, which are performed by bodily labour — the arts generally known as banausic or manual [...]. The former includes medicine, rhetoric, music, geometry, mathematics, arithmetic, astronomy, grammar, and jurisprudence. The arts of sculpture and drawing may also be included [among the high arts]: though they are manual in their performance, they do not require the strength of a young man in his prime”.
Galen’s classification of the arts:
- High arts
- Medicine
- Rhetoric
- Music
- Geometry
- Mathematics
- Arithmetic
- Astronomy
- Grammar
- Jurisprudence
- Sculpture
- Drawing
- Manual arts
5.13 Sextus Empiricus (c. 160 – c. 210)
Sextus was a Pyrrhonian skeptic, possibly from Egypt, who lived in the late 2nd and early 3rd Centuries CE (see, e.g., Floridi 2002). He wrote two sequences of works, both known by the same general title Pros mathematikous (Adversus mathematicos; Against the Mathematicians, Against the Theoreticians, or Against the Learned). The six books in the first sequence are commonly known collectively as Against the Professors, or Against Those in the Disciplines: they consist of Against the Grammarians; Against the Rhetoricians; Against the Geometers; Against the Arithmeticians; Against the Astrologers; and Against the Musicians. The five books in the second sequence are commonly known collectively as Against the Dogmatists: they consist of Against the Logicians, Books I and II; Against the Physicists, Books I and II; and Against the Ethicists. In this structure, therefore, the disciplines are divided into nine: grammar, rhetoric, geometry, arithmetic, astrology, music, logic, physics, and ethics.
Sextus’s classification of the sciences:
- Grammar
- Rhetoric
- Geometry
- Arithmetic
- Astrology
- Music
- Logic
- Physics
- Ethics
Sextus’s scheme effectively combines three other classifications:
- grammar, rhetoric, and logic correspond to the three sciences making up the trivium;
- geometry, arithmetic, astrology, and music correspond to the four sciences making up the quadrivium; and
- logic, physics, and ethics correspond to the three parts of philosophy in the Xenocratean/Stoic tradition.
The position of logic in the sequence prioritizes the integrity of philosophy over that of the trivium.
5.14 Flavius Philostratus (c. 170 – c. 250)
For much of the 20th Century, controversy abounded over the nature of the distinction to be made, if any, between up to four 3rd-century sophistic writers named Philostratus (see, e.g., Miles 2017). It was thought for a time that the author of a work cited by Tatarkiewicz (1963, 240) — the Gymnasticus — was possibly a nephew of Flavius Philostratus known as Philostratus the Elder (a.k.a. Philostratus of Lemnos; c. 190 – c. 230). The current consensus, however, is that the Gymnasticus was in fact written by Flavius Philostratus (a.k.a. Philostratus the Athenian; c. 170 – c. 250).
König (2009, 260 [emphasis added]) translates the first few lines of the Gymnasticus as follows: “Let us consider the following things as examples of wisdom [σοφία / sophia] — things like philosophy and speaking artfully and undertaking poetry and music and geometry, and even astronomy, as long as you don’t overdo it, and also the art of organizing armies, and even things like the following: the whole of medicine and painting and modelling, and all types of sculpting and gem-cutting and metal-engraving”. Philostratus then lists a selection of manual trades [βάναυσοι / banausoi] before categorizing gymnastikē (König 2009, 261): “I consider gymnastikē a form of sophia, and one which is inferior to none of the other arts [τέχναι / technai], so much so that treatises have been composed on the subject for the benefit of those who may wish to take up training”.
Tatarkiewicz (1963, 240) suggests that “[t]his was, perhaps, the first time in antiquity that fine arts [i.e., poetry, music, painting, sculpture] were assembled and enumerated” and “[f]or the first time [...] given a common name [sophia]” alongside various sciences. Tatarkiewicz contrasts the negative criterion used to identify the liberal arts — production free from physical effort — with the positive criterion used to identify wisdom — production demanding mental effort — and credits Philostratus for “assembl[ing] all the fine arts under one conception”.
Philostratus’s classification of the arts:
- Wise arts
- Philosophy
- Speaking artfully
- Poetry
- Music
- Geometry
- Astronomy
- Organizing armies
- Medicine
- Painting
- Modelling
- Sculpting
- Gem-cutting
- Metal-engraving
- Gymnastics
- Manual trades
5.15 Plotinus (c. 204 – 270)
The influential philosopher Plotinus, who was born in Egypt, is widely considered the founder of Neoplatonism (a 19th-Century invention indicating a supposedly new phase in the Platonic tradition; see, e.g., Gerson 2018).
Plotinus offers two separate classifications of the arts. One is to be found in On Difficulties About the Soul II (Ennead IV, 4), where he distinguishes two classes of arts “in terms of their operational principle and method”, then further subdivides the second group into two subclasses “[d]epending upon the nature of the object” (Panaiotidi 2014, 395). We might say that the former division distinguishes productive arts (focused on creating objects) from practical arts (focused on bringing about a qualitative change), while the latter subdivision distinguishes “natural” arts (which “help natural things to be in a natural state”; Plotinus 1984a, 229, 231, para. 31) from “psychagogic” arts (to use Tatarkiewicz’s term, 1963, 237; which aim at changing a person’s mental state).
We must, then, take a general view of all actions and experiences which occur in the whole universe, both the ones which are called natural and those which come about by art: we must say that [...] in those which come about by art the art either ends as it began, in the products of art, or brings in natural powers to help in producing acts and experiences which belong to the works of nature [...]. As for the arts, those which produce a house and the other products of art terminate in these; but the arts of medicine and agriculture and others of this kind are ancillary and help natural things to be in a natural state; but rhetoric and music and all the class of arts which influence the soul must be said to lead men to be better or worse by changing them; in these we must enquire how many they are and what is the power they have” (Plotinus 1984a, 229, 231, para. 31 [emphases added]; see also Panaiotidi 2014, 395–396).
Plotinus’s first classification of the arts (from Ennead IV, 4):
- Productive arts
- Architecture
- Practical arts
- “Natural” arts
- Medicine
- Agriculture
- “Psychagogic” arts
- Rhetoric
- Music
- “Natural” arts
Plotinus’s other classification of the arts — “in a sense the most complete of all classifications inherited from ancient times” (Tatarkiewicz 1963, 237) — is to be found in On Intellect, the Forms, and Being (Ennead V, 9). In this treatise, Plotinus asks: What things in the sensible world have their origin in the intelligible world? Using degree of involvement with the intelligible world as the principle of division, this time Plotinus distinguishes four classes of arts (Panaiotidi 2014, 393–395; see also Whitney 1990, 46–48): imitative (or mimetic), productive (or poietic), practical (subdivided into two groups, as before), and theoretical (or intellectual).
As for all the imitative arts, painting and sculpture, dancing and mime, which are in some way composed of elements from this world and use a model perceived by sense and imitate the forms and movements and transpose into their own terms the proportions which they see, it would not be reasonable to trace them back to the intelligible world except as included in the forming principle of man. But if any artistic skill starts from the proportions of [individual] living things and goes on from there to consider the proportions of living things in general, it would be a part of the power which also in the higher world considers and contemplates universal proportion in the intelligible. And certainly all music, since the ideas which it has are concerned with rhythm and melody, would be of the same kind, just like the art which is concerned with intelligible number. And as for the arts which produce artificial sense-objects, for instance building and carpentry, in so far as they make use of proportions, they would have their principles from the intelligible world and the practical thinking there; but since they mix these up with what is perceived by the senses they would not be altogether in the intelligible world, except in the [Form of] man. There would certainly not be farming there which helps the plants of the sense-world to grow, or medicine which has as its object of contemplation health here below, or the art which is concerned with strength and good bodily condition; for power in the intelligible world is different, and so is the health by which all living things there are undisturbed and adequate. And rhetoric and generalship, and the arts of administration and kingship, if any of them communicate excellence in the field of action, supposing that they contemplate that intelligible excellence, they have some part for their knowledge derived from the knowledge there. And since geometry is concerned with intelligibles, it must be placed there, and wisdom, which is on the highest level and concerned with being. (Plotinus 1984b, 311; 313; 315, para. 11 [emphases added])
Plotinus’s second classification of the arts (from Ennead V, 9):
- Imitative arts
- Painting
- Sculpture
- Dance
- Mime
- Productive arts
- Building
- Carpentry
- Practical arts
- “Natural” arts
- Farming
- Medicine
- “Psychagogic” arts
- Rhetoric
- Generalship
- Administration
- Kingship
- Music
- Number
- Geometry
- Wisdom
Echoing our suggestion that Pliny’s organizing principle seems to be one of decreasing levels of complexity (see above, Section 5.7; see also Kleineberg 2017), Whitney (1990, 48) argues that “[t]he overall graduated arrangement in these classifications reflects Plotinus’s conception of the universe as a series of levels of reality or being”.
6. Late Antiquity (c. 250–600)
6.1 “Maximus Victorinus” (4th century?)
James Zetzel (2018) writes that “the name Victorinus is attached to several late antique grammatical texts, possibly because of the famous Marius Victorinus [fl. 4th Century]. Victorinus, or Maximus Victorinus, may be a real person; but he is not necessarily the same person as Marius Victorinus, nor is he necessarily one person”. His name is included in the present survey because of the text attributed to “Maximus Victorinus” by Heinrich Keil and included in volume 6 of the compilation Grammatici Latini, first published in 1874. The text, Ars Victorini grammatici, contains a classification scheme that divides the arts into physical arts, intellectual arts, and “those requiring both human faculties” (Whitney 1990, 46):
What is art? How many are the kinds of art? Three. What are they? Certain ones are of the soul, certain ones are of the body, certain ones are of the soul and body. Which ones are only of the soul? These are poetry, music, astrology, grammar, rhetoric, law, philosophy. Which are of the body? Shouting, leaping, fleetness, carrying burdens. Which are of the soul and body? Cultivation of a farm, gymnastics, medicine, mechanics, carpentry.
“Victorinus”’s classification of the arts:
- Arts of the soul
- Poetry
- Music
- Astrology
- Grammar
- Rhetoric
- Law
- Philosophy
- Arts of the body
- Shouting
- Leaping
- Fleetness
- Carrying burdens
- Arts of the soul and body
- Agriculture
- Gymnastics
- Medicine
- Mechanics
- Carpentry
6.2 Augustine of Hippo (354–430)
Saint Augustine, born in a 4th-Century Roman community in what is now Algeria, was “perhaps the greatest Christian philosopher of Antiquity and certainly the one who exerted the deepest and most lasting influence” (Tornau 2019). In book 2, paras. 24–52, of De ordine (On Order), a work about the origin and role of evil (Augustine 1942), Augustine outlines a course of study that is “the earliest surviving presentation of the medieval curriculum with its seven liberal arts” (Kenyon 2012, 107). He discusses, in order, grammar, dialectic, rhetoric, music, geometry, and astrology, with number (i.e., arithmetic) as a connecting thread. He states (Augustine 1942, book 2, para. 44) that “all the liberal arts are learned partly for practical use and partly for the knowledge and contemplation of things”. Augustine planned to write a series of seven books, one for each art; he completed two, On Music and On Grammar, of which only the former has survived.
Augustine (1942, book 2, para. 47) allows that students can tackle basic questions in philosophy and theology only if they first complete the study of dialectic and/or arithmetic: “[N]o one ought to aspire to knowledge of those [philosophical] matters without that twofold science, so to speak, — the science of right reasoning [i.e., dialectic] and that of the power of numbers [i.e., arithmetic]. And if anyone thinks that this is indeed a great deal, let him master either numbers alone or only dialectics”. Kenyon (2012, 108) raises the possibility that the references here are to the full trivium (i.e., the sciences of the word) and quadrivium (i.e., the sciences of number).
Augustine’s curriculum:
- Grammar
- Dialectic
- Rhetoric
- Number
- Music
- Geometry
- Astrology
Likely influenced by Plotinus (Whitney 1990, 49), Augustine (1958, 63, chap. 27, para. 41) provides in De doctrina Christiana a classification of arts that “pertain to the corporal senses” as opposed to reason:
Among other [corporeal] arts some are concerned with the manufacture of a product which is the result of the labor of the artificer, like a house, a bench, a dish, or something else of this kind. Others exhibit a kind of assistance to the work of God, like medicine, agriculture, and navigation. Still others have all their effect in their proper actions, like dancing, running, and wrestling [...]. A knowledge of these arts is to be acquired casually and superficially in the ordinary course of life. (Augustine 1958, 66, chap. 30, para. 47 [emphases added])
This scheme is notable for its use of a scale from the physical to the spiritual as its organizing principle, and for the inclusion of medicine and agriculture in the most spiritual of the classes. Whitney (1990, 50) suggests that “[b]oth Augustine and Plotinus, as well as Plato [...] place a higher value on agriculture and medicine that on crafts in general because they connect human activity to nature and through nature to the divine”.
Augustine’s classification of the corporeal arts:
- Manufacture
- Architecture
- Carpentry
- Pottery
- Assistance to God
- Medicine
- Agriculture
- Navigation
- Action
- Dancing
- Running
- Wrestling
6.3 Martianus Minneus Felix Capella (fl. c. 410–420)
Born in what is now Algeria, Capella was a Latin prose writer in the early 5th Century (see, e.g., Stahl 1965). In his “popular and curious” (Weisheipl 1985, 206) allegorical work De nuptiis Philologiæ et Mercurii (On the Marriage of Philology and Mercury; Capella 1977), the seven liberal arts are brought as bridesmaids to the marriage in heaven, in this order: Grammar, Dialectic, Rhetoric, Geometry, Arithmetic, Astronomy, and Harmony. Capella was thus responsible for the canonical 5th-Century rendering of the seven disciplines (Hicks 2012), and was “instrumental in establishing the accepted enumeration of the seven liberal arts in the Middle Ages” (Weisheipl 1985, 206).
Capella’s curriculum:
- Grammar
- Dialectic
- Rhetoric
- Geometry
- Arithmetic
- Astronomy
- Harmony
6.4 Anicius Manlius Severinus Boëthius (c. 477–524)
Boethius was a Roman statesman and Christian philosopher, active in the early 6th century (see, e.g., Marenbon 2016). He was a man of “extraordinary learning and versatility [...] preserv[ing] the ideal of the classical Roman tradition [...] and [...] establish[ing] the foundation of Latin scholasticism” (Weisheipl 1985, 207).
Weisheipl (1985, 208–209 [emphases added]) describes how Boethius divides philosophy “into two species, theoretical and practical, that is speculative and active”. In turn, Boethius divides practical philosophy “into three branches: the study of personal morality, political morality, and domestic morality”, and (in De Trinitate, written around 520) divides speculative philosophy in what would become “the standard tripartite classification” of the medieval period: physics, mathematics, and theology. Of logic, Boethius writes (quoted in Weisheipl 1985, 209) that it is “not a part of philosophy but rather an instrument” of philosophy.
Weisheipl (1985, 210) argues that “[t]he Boethian division and designation of the philosophical sciences is clearly a fusion of Platonic and Aristotelian views. The division between speculative and practical [... is] Aristotelian. The tripartite hierarchy of forms suitable for speculative consideration, the position and division of mathematics are purely Platonic and Pythagorean”.
Boethius’s division of philosophy:
- Practical philosophy
- Ethics
- Domestics
- Politics
- Speculative philosophy
- Physics
- Mathematics
- Theology
Two of Boethius’s aims with his De institutione arithmetica, written around 500, were to make a Latin translation of Nicomachus’s Arithmētikē eisagōgē, and “to carry out some modifications of that text that he considered necessary to make it clearer and easier for the reader to understand” (Guillaumin 2012, 135). In book 1, chapter 1 (“Proemium, in quo divisio mathematicae”), we find the following outline of the quadrivium:
Among all the men of ancient authority who, following the lead of Pythagoras, have flourished in the purer reasoning of the mind, it is clearly obvious that hardly anyone has been able to reach the highest perfection of the disciplines of philosophy unless the nobility of such wisdom was investigated by him in a certain four-part study, the quadrivium, which will hardly be hidden from those properly respectful of expertness [...]. [A]rithmetic considers that multitude which exists of itself as an integral whole; the measures of musical modulation understand that multitude which exists in relation to some other; geometry offers the notion of stable magnitude; the skill of astronomical discipline explains the science of moveable magnitude. If a searcher is lacking knowledge of these four sciences, he is not able to find the true; without this kind of thought, nothing of truth is rightly known [...]. This, therefore, is the quadrivium by which we bring a superior mind from knowledge offered by the senses to the more certain things of the intellect. (Boethius 1983, 71–73 [emphases added])
Both Weisheipl (1985, 210) and Chadwick (1981, 71–73) make clear that the four disciplines are viewed by Boethius as forming a progressive sequence — i.e., that arithmetic must be studied before music, music before geometry, and geometry before astronomy. Only if the mathematical sciences are studied in this order may wisdom be acquired.
Boethius’s curriculum in mathematics:
- Arithmetic
- Music
- Geometry
- Astronomy
Boethius was the first writer to use the Latin term quadrivium (“place where four roads meet”) to render Nicomachus’s Greek expression téssares méthodoi (“the four methods”), in imitation of the Latin word bivium, which designates the meeting-place of two roads [13]. The term trivium came into currency later (around the 9th Century) to denote the meeting-place of the three literary arts of grammar, rhetoric, and dialectic (see, e.g., Rajna 1928). The sum of the quadrivium and trivium “designated the meeting in two blocks of the seven sciences of neo-Platonic encyclopedism” (Guillaumin 2012, 137).
6.5 Flavius Magnus Aurelius Cassiodorus Senator (490 – c. 585)
Cassiodorus was a Roman statesman and (later) a Christian monk in the 6th Century CE (see, e.g., Jones 1945). With his Institutiones divinarum et saecularium litterarum (Institutes of Divine and Secular Literature), written around 545 as a manual for the monks of Vivarium, the goal was to show how “the unbroken line of the Divine Scriptures and the compendious knowledge of secular letters might [...] be related” (Cassiodorus Senator 1966, 67, book 1, para. 1) [14]. The first book is a compendium of divine scriptures; the second, “which became exceedingly popular in later centuries” (Weisheipl 1985, 211), is a summary of the seven liberal arts.
In the Preface to book 2 (Cassiodorus Senator 1966, 143–144, book 2, para. 4 [emphases added]), Cassiodorus previews the order in which he will discuss the seven liberal arts:
In this book we must speak first of the art of grammar, which is manifestly the source and foundation of liberal studies [...]. Second, we must speak of the art of rhetoric, which is deemed very necessary and honorable because of the splendor and fullness of its eloquence, especially in civil questions. Third, we must speak of logic, which is called dialectic; [...] this study separates the true from the false by means of very subtle and concise reasoning. Fourth, we must speak of mathematics, which embraces four sciences, to wit, arithmetic, geometry, music, and astronomy. In Latin we may call mathematics the theoretical study; though we might apply this term to all studies which teach one to speculate on abstract principles, nevertheless, by reason of its excellence this study has claimed the common word strictly for itself.
Cassiodorus’s curriculum:
- Divine scripture
- Grammar
- Rhetoric
- Dialectic
- Arithmetic
- Geometry
- Music
- Astronomy
It is notable that, for Cassiodorus, “the practice of medicine and agriculture is an act of charity” and comes under the heading of divine scripture (Whitney 1990, 44).
6.6 Isidore of Seville (c. 560 – 636)
Isidore was a Spanish theologian who served as Archbishop of Seville for more than thirty years at the beginning of the 7th Century (see, e.g., Castellanos 2019). His etymological encyclopedia Etymologiae (a.k.a. Origines) assembled passages from hundreds of classical sources that might otherwise have been lost, and “enjoyed great popularity as a reference work throughout the Middle Ages” (Weisheipl 1985, 212). Two classification schemes are outlined in this work.
In book I (De grammatica), chapter ii (De septem liberalibus disciplinis), he provides an outline of the seven liberal arts:
There are seven disciplines of the liberal arts. The first is grammar, that is, skill in speaking. The second is rhetoric, which, on account of the brilliance and fluency of its eloquence, is considered most necessary in public proceedings. The third is dialectic, otherwise known as logic, which separates the true from the false by very subtle argumentation. The fourth is arithmetic, which contains the principles and classifications of numbers. The fifth is music, which consists of poems and songs. The sixth is geometry, which encompasses the measures and dimensions of the earth. The seventh is astronomy, which covers the law of the stars. (Isidore 2006, 39 [emphases added])
Isidore’s curriculum:
- Grammar
- Rhetoric
- Dialectic
- Arithmetic
- Music
- Geometry
- Astronomy
In book II (De rhetorica et dialectica), chapter xxiv (De definition philosophiae), Isidore discusses a scheme that combines the liberal arts with the Xenocratean/Stoic division of philosophy, aligning the quadrivium with physics, and much of the trivium with logic:
There are three kinds of philosophy: one natural (naturalis), which in Greek is ‘physics’ (physica), in which one discusses the investigation of nature; a second moral (moralis), which is called ‘ethics’ (ethica) in Greek, in which moral behavior is treated; a third rational (rationalis), which is named with the Greek term ‘logic’ (logica), in which there is disputation concerning how in the causes of things and in moral behavior the truth itself may be investigated [...]. Plato divided physics into four categories: arithmetic, geometry, music, and astronomy [...]. [Socrates] divided ethics into the four virtues of the soul, namely prudence, justice, fortitude, and temperance [...]. Plato added logic, which is called rational philosophy [...]. [He] divid[ed] logic into rhetoric and dialectic”. (Isidore 2006, 79–80 [emphases added]) [15]
Isidore’s division of philosophy:
- Physics
- Arithmetic
- Geometry
- Music
- Astronomy
- Ethics
- Prudence
- Justice
- Fortitude
- Temperance
- Logic
- Rhetoric
- Dialectic
7. Analysis
In the tables that follow, entries are italicized for schemes that are attributed to authors by doxographic or modern secondary resources without supporting evidence among the original authors’ surviving works, and emboldened for schemes that are presented explicitly as classifications by the authors of primary sources. Entries that are neither italicized nor emboldened represent schemes that, while appearing in the primary sources, can be identified only implicitly as functional classifications. The numbers in the various columns of each table indicate the orders in which different sciences are specified in the classifications represented by each entry: in Table 2 for example, the first entry shows that Theodorus is said to have specified Geometry first, Astronomy second, Arithmetic third, and Music fourth. It should be noted that the order in which an author mentions the different sciences in a text does not necessarily indicate the order in which that author intends for those sciences to be studied. In cases where an author is responsible for more than one classification scheme, numbers in parentheses next to authors’ names indicate the particular classification schemes that are the subjects of the corresponding entries: “(1)” indicates the first scheme covered under the author’s name in the survey above, “(2)” indicates the second, and so on. Numbers in square brackets — “[1]”, “[2]”, etc. — refer to endnotes.
Table 2 shows the main adherents to the idea of téssares méthodoi (the Greek term used first by Nicomachus) or quadrivium (the Latin term used first by Boethius). Theodorus may have been one of the first to divide up the mathematical sciences in this way (see above, Section 2.4); the idea certainly seems to have emerged out of Pythagoreanism in the 5th Century BCE.
Table 2: The development of the quadrivium
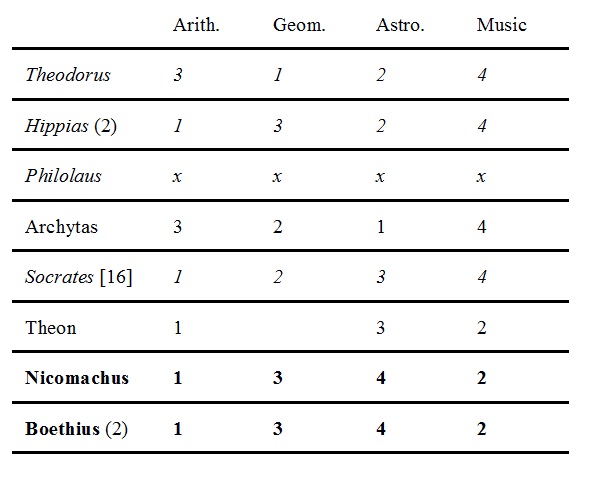
Table 3 lists in chronological order the authors who were primarily concerned to define the boundaries of philosophy as an area of study. The basic tripartite division is into logic (or dialectic), physics (including mathematics and natural science), and ethics; this conception appears to have arisen in the 4th Century BCE, probably at the Academy, probably while Xenocrates was its head (see above, Section 3.4), possibly under Aristotelean influence (see above, Section 3.5), and possibly even reflecting Plato’s ideas about the parts of the soul (see above, Section 3.2). Associated later with the Stoics (see above, Sections 4.2 and 4.3), we have referred to it as the Xenocratean/Stoicist conception of philosophy.
Table 3: Classifications of the branches of philosophy
Table 4 similarly lists those who were responsible (or supposedly so, in the case of Plato) for a particular conception of the sciences that distinguishes theoretical, practical, and productive sciences. (Included in this table are also entries for schemes that distinguish the arts in a similar fashion.) This tripartite classification of the sciences is traditionally regarded as Aristotelean, for good reason (see above, Section 3.5). It is a classification of knowledge that “did not pass a moral judgment on different human activities but instead assumed the rationality of all arts and grouped them according to the kind of process each involved” (Whitney 1990, 32), supplying “a flexible and useful method of organizing all branches [...] which lent itself to later elaboration and expansion” (Whitney 1990, 35).
The notion of “productive arts” seems to have died out in the Latin West sometime after the 5th Century CE (Whitney 1990, 39). Whitney (1990, 40) suggests that “[t]he disappearance of the threefold division of knowledge into productive, practical and theoretical knowledge perhaps reflected the increasing unavailability of the Aristotelian corpus as a whole in the Latin West”, and points out that “[a] symptom of the resulting confusion is the lack of any standard Latin translation for ποιητικάι”.
Table 4: Aristotelean classifications of the sciences and arts
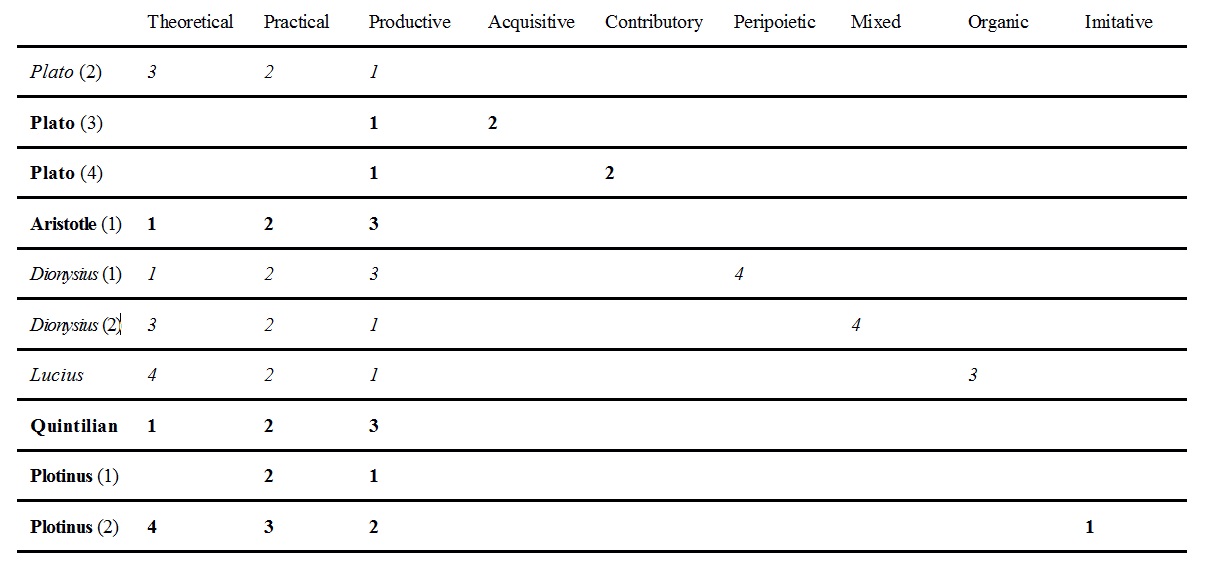
Table 5 contains entries for other classifications of the arts suggested by the authors (or their commentators) in our survey. Two recurring distinctions are those made (A) between the useful and the pleasurable, first expressed perhaps by Isocrates (see Section 3.1), and (B) between the vulgar (a.k.a. banausic, common, illiberal, low, manual, mechanical, sordid) and liberal (a.k.a. free, high, noble, rational, sophistic). As Tatarkiewicz (1963, 237 [emphases in original]) points out, the principle of division used by the former is “the aim of arts”; that used by the latter is “the point of view of the activity (mental or physical) which was required of those who cultivated them”.
The distinction between vulgar and liberal arts was first identified maybe by Posidonius, if Seneca is to be believed (see Section 5.2), although Tatarkiewicz (1963, 233) thinks that it “appeared in antiquity very early, so early that it is impossible to indicate its author”. It was “[t]he classification of arts best known and most generally accepted in ancient times” (Tatarkiewicz 1963, 233) and, “more than any other ancient classification, dependent on the historical and social conditions of Greece” (Tatarkiewicz 1963, 233). One outcome of the Greek tendency to look down upon physical work and to hold mental activity in higher esteem was a hierarchical model of the arts, in which some were viewed as superior (not just different) to others. As Whitney (1990, 27) explains, “[w]hen authors wished to emphasize the physical and inferior character of all or some crafts, they labeled these crafts as banausic (βάναυσος), a pejorative term which served to separate unworthy from worthy arts”. Terms such as this were used “as general labels for arts or trades which supply merely necessary needs or have degrading effects on their practitioners, whether because they deform the body, involve the transfer of money or encourage immoral behavior” (Whitney 1990, 30). In other words, “[t]he banausic arts included not only manual arts but any activity which was pursued for physical need or pleasure, entertainment or monetary gain” (Whitney 1990, 42). In contrast (Whitney 1990, 28), “[t]he liberal arts were those arts pursued for the sake of a liberated mind rather than for the satisfaction of any vocational or physical need”. They were “not a fixed canon of disciplines but a loosely defined group of arts characterized in terms of their function and value in society” (Whitney 1990, 42).
As Whitney (1990, 51) points out, “the strongest and clearest” classifications that adopted a hierarchical arrangement of arts — from the most physical to the most intellectual or spiritual — were “made by thinkers deeply influenced by Platonic or Neoplatonic thought”, such as Plotinus, “Victorinus”, and Augustine.
Table 5A: Other classifications of the arts, part A

Table 5B: Other classifications of the arts, part B
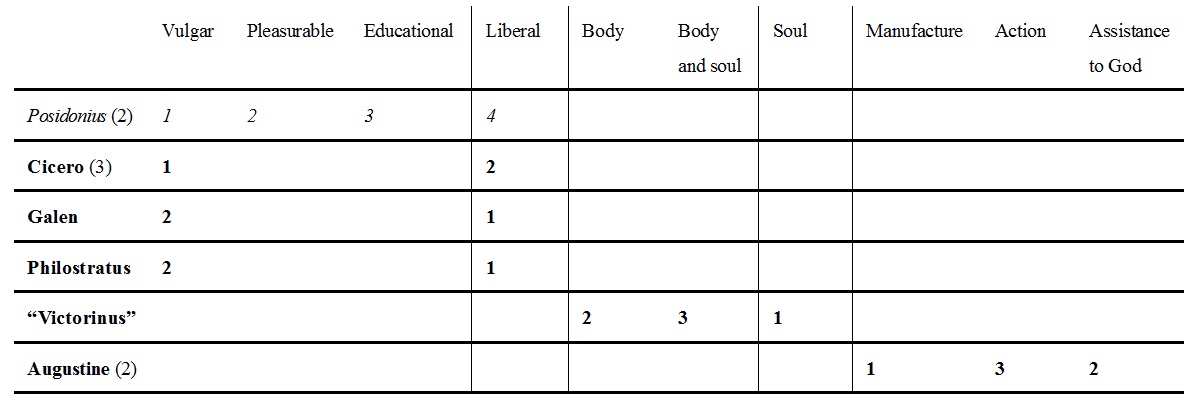
Table 6 charts the extension of the quadrivium into a full curriculum of liberal arts (artēs liberales), the latter term first used by Cicero. The liberal arts curriculum corresponds to a large extent with that indicated by the Greek term ἐγκύκλιος παιδεία / enkýklios paideía, which is the root of the English word encyclopedia, but which is also used to refer to a large compendium of general education, of which the liberal arts curriculum is the primary example [17]. By Capella’s time, this curriculum had solidified into seven subjects — the four mathematical sciences plus grammar, rhetoric, and dialectic (or logic) — and specific orders for study were being specified, usually with the three verbal arts preceding mathematics (West 1892). The term trivium was not used to refer to the verbal arts until the 9th Century, but the seven subjects comprising the trivium and quadrivium were to go on to serve as the most common structure for early medieval Western university education, and to form the basis for conceptions of liberal higher learning for centuries.
Table 6: The emergence of the liberal arts
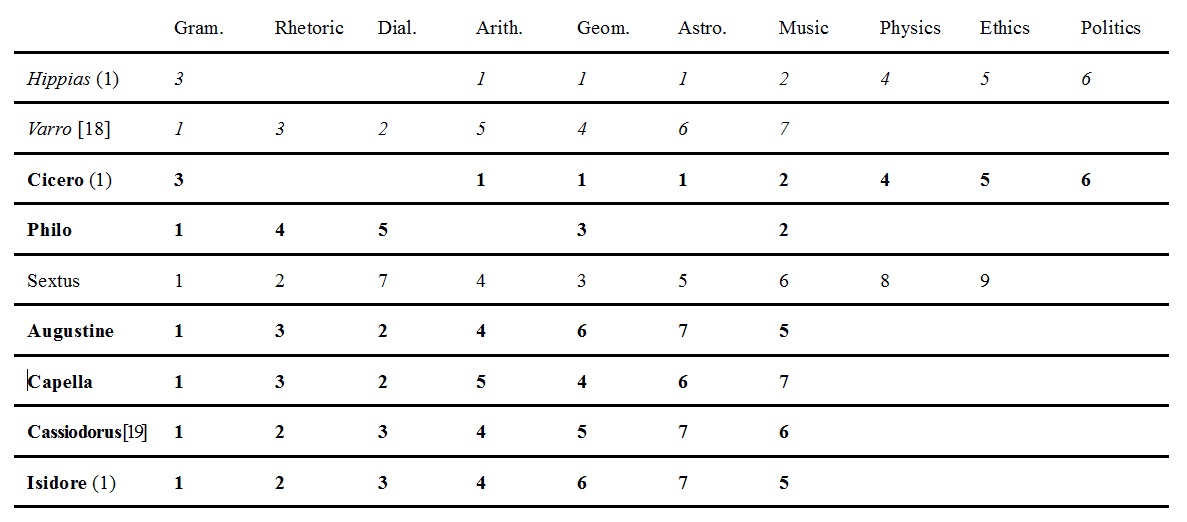
A remaining question relates to the relationships between the systems listed in different tables. The nature of the relationship between the quadrivium (Table 4) and the full liberal arts curriculum (Table 5) is straightforward, of course; but is there a general connection to be found, for example, between the division of philosophy into logic, physics, and ethics on the one hand, and the classification of the sciences into theoretical, practical, and productive on the other? Or between either of those divisions and the quadrivium/liberal arts? It appears that any connections are to be revealed on a case-by-case basis. Aristotle’s scheme, for example, breaks down into mathematics, physics, and theology (theoretical); politics and ethics (practical); and music and rhetoric, among others (productive); with logic in a class of its own. Collectively, these subjects form an expanded liberal arts curriculum, with only grammar missing from the canonical seven; and the relationship between Logic–Physics–Ethics and Logic–Theoretical–Practical should be clear.
8. Conclusion
In conclusion, it remains for us to highlight the major findings heralded in Section 1 and reiterated in Section 7:
- The division of mathematics into the four subjects of (what became known as) the quadrivium emerged out of 5th-Century Pythagoreanism and remained standard into the medieval period.
- The tripartite division of philosophy into logic, physics, and ethics emerged out of 4th-Century Athens and also remained standard into the medieval period.
- Aristotle’s tripartite division of the sciences into theoretical, practical, and productive enjoyed great influence over others’ efforts to classify the sciences and arts, but was not directly reflected in the principles used to build curricula of study.
- Such curricula, of “liberal arts”, emerged during the Roman period and consisted of what would become known as the quadrivium and (much later) the trivium.
- Some attempts were made to merge quadrivium/trivium-based classifications with the tripartite division of philosophy: cf. especially Cicero (see Section 5.5), Sextus (see Section 5.13), and Isidore (see Section 6.6).
- Weisheipl (1985, 213) remarks that “St. Augustine, Boethius, Cassiodorus, and St. Isidore served as the principal sources for all later discussion of the seven liberal arts and the tripartite division of philosophy”.
- Finally, it is clear that “classification of the arts and sciences became increasingly detailed and elaborate over the course of time” (Whitney 1990, 50).
Because they do not deal specifically with the classification of philosophical knowledge, or with the fields of study required to master philosophical learning, the schemes of Callimachus (see Section 4.4) and Pliny (see Section 5.7) are outliers in this survey. Since they differ so greatly in content (if not in form) from the schemes for the construction of educational curricula, they are not represented in any of the tables in Section 7. As the period of Late Antiquity moves into that of the Early Middle Ages (600–1000) and the establishment of monastic libraries, we begin to see more instances of schemes for the classification of general collections of books or parts of books. A forthcoming IEKO entry will continue the story.
Acknowledgments
The author would like to thank Birger Hjørland and two anonymous reviewers for their prodigious efforts in providing comments on an earlier draft of this entry.
Endnotes
1. The parts of Richardson’s work that are relevant to the period covered by the present paper are on pp. 49–54 and pp. 89–90.
2. The ancient concept of “physics” is markedly different from the modern one. The original meaning of the Greek φύσις / phúsis, from which φυσική / phusikḗ is derived, is “nature”; and ancient “physics” should thus be interpreted as equivalent to “natural science”, including botany, zoology, and psychology.
3. The author is indebted to an anonymous reviewer for making this point.
4. Tatarkiewicz (1963, 232–233) combines the treatment at Sophist 219a–c with the statement at Republic 601d that “there are some three arts concerned with everything, the user’s art, the maker’s, and the imitator’s” (Plato 1961b, 826) in order to argue that Plato’s classification consists of three (not two) classes of arts with “different relations to real things”: “[acquisitive] arts which make use of reality, [productive] arts which produce a new reality, and [imitative] arts which imitate reality” (emphases in original).
5. Plato’s conception of “music” also included poetry and declamation. “In Graeco-Roman antiquity, performing arts were grouped under a single inclusive term: the Greek word mousikē (sc. technē), and its Latin calque ars musica. These terms allude to a much broader notion than their modern counterparts: they embraced many artistic activities (song, dance, poetry, instrumental accompaniments, or solos) and brought them all within the Muses’ domain” (Rocconi and Lynch 2020, 1). Cf. Liddell and Scott (1940): μουσική = “any art over which the Muses presided, esp. poetry sung to music”.
6. The author is indebted to an anonymous reviewer for making this point.
7. For some reason, Witty counts ten: “Ten classes of literature have been listed” (Witty 1958, p. 136).
8. For Varro and his contemporaries, astrologia (derived from the Greek ἀστρολογία) did not yet have the meaning of “prediction of events by the position of the stars”, but was synonymous with astronomia (Greek ἀστρονομία): “knowledge of the stars”.
9. Cf. Cicero 1948, 7, book 1, section 2, paras. 6–7: “For in whatever direction you turn your mind and thoughts, you will find very many excelling in every kind, not merely of ordinary arts [mediocrium artium], but of such as are almost the greatest [maximarum]”. Contrary to Tatarkiewicz’s account, nowhere in De Oratore does Cicero talk of “minor” arts.
10. The metaphorical title On Mating with the Preliminary Studies is a translation of the underlying Greek Peri tēs pros ta propaideumata synodou, which in turn reflects the nature of the work as an allegorical exegesis of the biblical Genesis 16:1–6. For a full explanation, see De Vries (2009).
11. The author is indebted to an anonymous reviewer for making the point that, only one sentence later, Philo (1932, 467, para. 18 [emphasis added]) admits that there exist important sciences other than the five just listed: “It is profitable then to take these and the like for our associates and for the field of our preliminary studies”. Elsewhere in the same text, Philo (1932, 463, para. 11) mentions a separate, differently ordered set of sciences in which he replaces dialectic with astronomy (later characterized by Philo [1932, 483, para. 50] as “the queen of sciences”): “Naturally, then, virtue will employ no minor kind of introduction, but grammar, geometry, astronomy, rhetoric, music, and all the other branches of intellectual study”. The danger in using one or other of the two lists to derive an entire curriculum should be clear.
12. The author is indebted to an anonymous reviewer for making the point that not all scholars agree that Pliny intended his work to be an example of enkýklios paideía. Doody (2009), for example, argues that the genre of encyclopedia did not exist in the ancient world, and that it was only in the early modern period that the Natural History came to be categorized as such.
13. The term bivium had been used, for example, literally by Pliny in his Natural History, book 6, para. 32 (“At Petra two roads meet”), and metaphorically by Varro in his On Agriculture, book 1, para. 18 (“For nature has given us two routes to agriculture, experiment and imitation”). It appears that the supposedly Pythagorean usage of bivium to indicate “that moment when one chooses either a materialistic or a spiritual way of life” (Kalina 2005, 38) is a medieval tradition in which the term “served as a metaphor for an individual’s free will [...] to choose between good and evil” (Kalina 2005, 39). The connection to Pythagoras derives from the “(pseudo- or neo-) Pythagorean motif of a mystical-magical interpretation of the letter Y” (Kalina 2005, 38).
14. The author is indebted to an anonymous reviewer for making the point that the study of “Divine scripture” is an essential initial element of Cassiodorus’s curriculum.
15. Isidore was wrong about the roles of Plato and Socrates in the subdivision of physics, ethics, and logic.
16. Socrates/Plato split Geometry into two — plane and solid — and also specified Gymnastics and Dialectic as elements of his curriculum.
17. Liddell and Scott (1940) record the following as primary English senses of ἐγκύκλιος: (1) “circular, round”; (II) “revolving in a cycle, recurrent”; (III) “ordinary, everyday”. The definition given of ἐγκύκλιος παιδεία is “general education, prior to professional studies”. Controversy has long surrounded the connotative role of “circular” or “(en)cyclical” (as opposed to “general” or “ordinary”) in such an expression, and whether the Greeks ever understood the term to mean anything like “circle/circuit/cycle of learning” or even “complete system of learning” in the way in which the English term “encyclopedia” is commonly defined (see, e.g., De Rijk 1965).
18. Varro also included Medicine and Architecture in his curriculum.
19. See note 14, above.
References
Acosta-Hughes, Benjamin, Luigi Lehnus and Susan Stephens. 2011. Brill’s Companion to Callimachus. Leiden: Brill.
Alesse, Francesca (ed.). 2008. Philo of Alexandria and Post-Aristotelian Philosophy. Leiden: Brill.
Amadio, Anselm H. and Anthony J. P. Kenny. 2020. “Aristotle”. In Encyclopædia Britannica. Chicago, IL: Encyclopædia Britannica. https://www.britannica.com/biography/Aristotle.
Archytas. 2005. Archytas of Tarentum: Pythagorean, Philosopher and Mathematician King, ed. Carl Huffman. Cambridge: Cambridge University Press.
Aristotle. 1984a. “Topics”, trans. W. A. Pickard-Cambridge. In Jonathan Barnes (ed.), The Complete Works of Aristotle, Vol. 1, 167–277. Bollingen Series, no. 71-2. Princeton: Princeton University Press.
Aristotle. 1984b. “Metaphysics”, trans. W. D Ross. In Jonathan Barnes (ed.), The Complete Works of Aristotle, Vol. 2, 1552–1728. Bollingen Series, no. 71-2. Princeton: Princeton University Press.
Augustine of Hippo. 1942. Divine Providence and the Problem of Evil: A Translation of St. Augustine’s De ordine, trans. Robert P. Russell. New York: Cosmopolitan Science & Art Service.
Augustine of Hippo. 1958. On Christian Doctrine, trans. D. W. Robertson, Jr. Indianapolis, IN: Bobbs-Merrill.
Baltzly, Dirk. 2018. “Stoicism”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/spr2019/entries/stoicism/.
Barker, Andrew. 2014. “Pythagorean Harmonics”. In Carl A. Huffman (ed.), A History of Pythagoreanism, 185–203. Cambridge: Cambridge University Press.
Bekker, Immanuel (ed.). 1816. Anecdota Graeca, vol. 2. Berlin: G. Reimer.
Boethius. 1983. Boethian Number Theory: A Translation of the De institutione arithmetica, trans. Michael Masi. Amsterdam: Rodopi.
Capella, Martianus. 1977. Martianus Capella and the Seven Liberal Arts, Volume II: The Marriage of Philology and Mercury, trans. William Harris Stahl & Richard Johnson with E. L. Burge. New York: Columbia University Press.
Cassiodorus Senator. 1966. An Introduction to Divine and Human Readings, trans. Leslie Webber Jones. New York: Octagon.
Castellanos, Santiago. 2019. “Isidore of Seville: Historical Contexts”. In Andrew Fear & Jamie Wood (eds.), A Companion to Isidore of Seville, 21–41. Leiden: Brill.
Chadwick, Henry. 1981. Boethius: The Consolations of Music, Logic, Theology, and Philosophy. Oxford: Clarendon Press.
Cicero. 1942. On the Orator: Book 3; On Fate; Stoic Paradoxes; Divisions of Oratory, trans. H. Rackham. Loeb Classical Library, no. 349. Cambridge, MA: Harvard University Press.
Cicero. 1948. De Oratore: Books I–II, trans. E. W. Sutton & H. Rackham, rev. ed. Loeb Classical Library, no. 348. Cambridge, MA: Harvard University Press.
Colson, F. H. and G. H. Whitaker. 1932. “Analytical Introduction [to On Mating with the Preliminary Studies]”. In Philo: Volume IV, 451–457. Loeb Classical Library, no. 261. Cambridge, MA: Harvard University Press.
Dancy, Russell. 2017. “Xenocrates”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/spr2017/entries/xenocrates/.
De Rijk, L. M. 1965. “Έγκύκλιος παιδεία: A Study of its Original Meaning”. Vivarium 3: 24–94.
De Vries, Hent. 2009. “Philosophia ancilla theologiae: Allegory and Ascension in Philo’s On Mating with the Preliminary Studies (De congress quaerendae eruditionis gratia)”. The Bible and Critical Theory 5, no. 3: 41.1–41.19.
Dillon, John. 1996. The Middle Platonists, 80 BC to AD 220, rev. ed. Ithaca, NY: Cornell University Press.
Diogenes Laertius. 2018. Lives of the Eminent Philosophers, trans. Pamela Mensch, ed. James Miller. New York: Oxford University Press.
Doody, Aude. 2009. “Pliny’s Natural History: Enkuklios Paideia and the Ancient Encyclopedia”. Journal of the History of Ideas 70, no. 1: 1–21.
Doody, Aude. 2010. Pliny’s Encyclopedia: The Reception of the Natural History. Cambridge: Cambridge University Press.
Dousa, Thomas M. 2018. “Library Classification, Part I: Introduction and Premodern Classification”. In Birger Hjørland & Claudio Gnoli (eds.), ISKO Encyclopedia of Knowledge Organization. https://www.isko.org/cyclo/library_classification.
Encyclopædia Britannica, Editors of the. 2017. “Hippias of Elis”. In Encyclopædia Britannica. Chicago, IL: Encyclopædia Britannica. https://www.britannica.com/biography/Hippias-of-Elis.
Evans, James and J. Lennart Berggren. 2007. Geminos’s Introduction to the Phenomena: A Translation and Study of a Hellenistic Survey of Astronomy. Princeton, NJ: Princeton University Press.
Fisher, Nicholas. 1990. “The Classification of the Sciences”. In R. C. Olby, G. N. Cantor, J. R. R. Christie and M. J. S. Hodge (eds.), Companion to the History of Modern Science, 853–868. London: Routledge.
Flint, Robert. 1904. Philosophy as Scientia Scientiarum; and, A History of Classifications of the Sciences. Edinburgh: W. Blackwood.
Floridi, Luciano. 2002. Sextus Empiricus: The Transmission and Recovery of Pyrrhonism. New York: Oxford University Press.
Galen. 1997. “An Exhortation to Study the Arts”. In Selected Works, trans. P. N. Singer, 35–52. Oxford: Oxford University Press.
Gerson, Lloyd. 2018. “Plotinus”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/fall2018/entries/plotinus/.
Gibson, Roy and Ruth Morello (eds.). 2011. Pliny the Elder: Themes and Contexts. Mnemosyne Supplementa, no. 329, Leiden: Brill.
Grafton, Anthony, Glenn W. Most and Salvatore Settis (eds.). 2010. The Classical Tradition. Cambridge, MA: Harvard University Press.
Guillaumin, Jean-Yves. 2012. “Boethius’s De institutione arithmetica and Its Influence on Posterity”. In Noel Harold Kaylor, Jr. and Philip Edward Phillips (eds.), A Companion to Boethius in the Middle Ages, 135–161. Leiden: Brill.
Guthrie, W. K. C. 1978. A History of Greek Philosophy, V: The Later Plato and the Academy. Cambridge: Cambridge University Press.
Haskins, Ekaterina V. 2004. Logos and Power in Isocrates and Aristotle. Columbia, SC: University of South Carolina Press.
Helmig, Christoph and Carlos Steel. 2020. “Proclus”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/fall2020/entries/proclus/.
Hicks, Andrew. 2012. “Martianus Capella and the Liberal Arts”. In Ralph Hexter & David Townsend (eds.), The Oxford Handbook of Medieval Latin Literature, 307–334. Oxford: Oxford University Press.
Hjørland, Birger. 2017. “Classification”. Knowledge Organization 44, no. 2: 97–128. [Also available in Birger Hjørland & Claudio Gnoli (eds.), ISKO Encyclopedia of Knowledge Organization. https://www.isko.org/cyclo/classification.htm.]
Huffman, Carl. 2016a. “Philolaus”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/sum2016/entries/philolaus/.
Huffman, Carl. 2016b. “Archytas”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/sum2018/entries/archytas/.
Huffman, Carl. 2018. “Pythagoras”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/win2018/entries/pythagoras/.
Isidore of Seville. 2006. The Etymologies of Isidore of Seville, trans. Stephen A. Barney, W. J. Lewis, J. A. Beach and Oliver Berghof. Cambridge: Cambridge University Press.
Isocrates. 1928. “Panegyricus”. In Isocrates: Volume I, trans. George Norlin, 115–241. Loeb Classical Library, no. 209. Cambridge, MA: Harvard University Press.
Jones, Leslie W. 1945. “The Influence of Cassiodorus on Mediæval Culture”. Speculum 20, no. 4: 433–442.
Kahn, Charles H. 2001. Pythagoras and the Pythagoreans: A Brief History. Indianapolis, IN: Hackett.
Kalina, Pavel. 2005. “Michelangelo, Pythagoras, and Panofsky”. Source: Notes in the History of Art 24, no. 3: 38–42.
Karamanolis, George. 2014. “Plutarch”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/sum2020/entries/plutarch/.
Keil, Heinrich (ed.). 1874. Grammatici Latini, vol. 6. Leipzig: B. G. Teubner.
Kennedy, George. “An Estimate of Quintilian”. American Journal of Philology 83, no. 2: 130–146.
Kenyon, Erik. 2012. “Augustine and the Liberal Arts”. Arts and Humanities in Higher Education 12, no. 1: 105–113.
Kidd, I. G. 1988. Posidonius, Volume II: The Commentary; (i) Testimonia and Fragments 1–149. Cambridge: Cambridge University Press.
Kleineberg, Michael. 2017. “Integrative Levels”. Knowledge Organization 44, no. 5: 349–379. [Also available in Birger Hjørland & Claudio Gnoli (eds.), ISKO Encyclopedia of Knowledge Organization. https://www.isko.org/cyclo/integrative_levels.]
König, Jason. 2009. “Training Athletes and Interpreting the Past in Philostratus’ Gymnasticus”. In Ewen Bowie & Jas Elsner (eds.), Philostratus, 251–283. Cambridge: Cambridge University Press.
Konstan, David. 2018. “Epicurus”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/sum2018/entries/epicurus/.
Kraut, Richard. 2017. “Plato”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/fall2017/entries/plato/.
Law, Vivien. 1990. “Roman Evidence on the Authenticity of the Grammar Attributed to Dionysius Thrax”. In Hans-Josef Niederehe & Konrad Koerner (eds.), History and Historiography of Linguistics: Papers from the Fourth International Conference on the History of the Language Sciences (ICHoLS IV) (Trier, August 24–28, 1987), vol. 1, 89–96. Amsterdam: John Benjamins.
Liddell, Henry George and Robert Scott. 1940. A Greek–English Lexicon, rev. Henry Stuart Jones with Roderick McKenzie. Oxford: Clarendon Press.
Lloyd, Geoffrey. 1987. “The Alleged Fallacy of Hippocrates of Chios”. Apeiron 20, no. 2: 103–128.
Lloyd, Geoffrey. 2014. “Pythagoras”. In Carl A. Huffman (ed.), A History of Pythagoreanism, 24–45. Cambridge: Cambridge University Press.
Long, A. A. 1986. Hellenistic Philosophy: Stoics, Epicureans, Sceptics, 2nd ed. Berkeley, CA: University of California Press.
Mansfeld, Jaap. 2016. “Doxography of Ancient Philosophy”. In Edward N. Zalta, (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/win2016/entries/doxography-ancient/.
Marenbon, John. 2016. “Anicius Manlius Severinus Boethius”. In Edward N. Zalta, (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/win2016/entries/boethius/.
Marrou, H. I. 1956. A History of Education in Antiquity, trans. George Lamb. New York: Sheed and Ward.
Meinwald, Constance C. 2020. “Plato”. In Encyclopædia Britannica. Chicago, IL: Encyclopædia Britannica. https://www.britannica.com/biography/Plato.
Miles, Graeme. 2017. “Philostratus”. In Daniel S. Richter & William A. Johnson (eds.), The Oxford Handbook to the Second Sophistic, 273–289. Oxford: Oxford University Press.
Mueller, Ian. 1991. “Mathematics and Education: Some Notes on the Platonic Program”. Apeiron 24, no. 4: 85–104.
Mueller, Ian. 2004. “Remarks on Physics and Mathematical Astronomy and Optics in Epicurus, Sextus Empiricus, and Some Stoics”. Apeiron 37, no. 4: 57–87.
Mutschmann, Hermann (ed.). 1906. Divisiones Quae Vulgo Dicuntur Aristoteleae. Leipzig: B. G. Teubner.
Nicomachus of Gerasa. 1926. Introduction to Arithmetic, trans. Martin Luther D’Ooge. New York: Macmillan.
Nutton, Vivian. 2020. “Galen”. In Encyclopædia Britannica. Chicago, IL: Encyclopædia Britannica. https://www.britannica.com/biography/Galen.
Panaiotidi, Elvira. 2014. “‘The Same Thing in Another Medium’: Plotinus’ Notion of Music”. Ancient Philosophy 34: 393–413.
Parry, Richard. 2020. “Episteme and Techne”. In Edward N. Zalta, (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/fall2020/entries/episteme-techne/.
Pellegrin, Pierre. 1986. Aristotle’s Classification of Animals: Biology and the Conceptual Unity of the Aristotelian Corpus. Berkeley, CA: University of California Press.
Petrucci, Federico M. 2017. “Theon of Smyrna: Re-Thinking Platonic Mathematics in Middle Platonism”. In Harold Tarrant, François Renaud, Dirk Baltzly and Danielle A. Layne (eds.), Brill’s Companion to the Reception of Plato in Antiquity, 143–155. Leiden: Brill.
Philo. 1932. “On Mating with the Preliminary Studies”. In Philo: Volume IV, trans. F. H. Colson & G. H. Whitaker, 458–551. Loeb Classical Library, no. 261. Cambridge, MA: Harvard University Press.
Plato. 1961a. “Protagoras”, trans. W. K. C. Guthrie. In Edith Hamilton & Huntington Cairns (eds.), The Collected Dialogues of Plato, 308–352. Bollingen Series, no. 71. New York: Pantheon.
Plato. 1961b. “Republic”, trans. Paul Shorey. In Edith Hamilton & Huntington Cairns (eds.), The Collected Dialogues of Plato, 575–844. Bollingen Series, no. 71. New York: Pantheon.
Plato. 1961c. “Sophist”, trans. F. M. Cornford. In Edith Hamilton & Huntington Cairns (eds.), The Collected Dialogues of Plato, 957–1017. Bollingen Series, no. 71. New York: Pantheon.
Plato. 1961d. “Statesman”, trans. J. B. Skemp. In Edith Hamilton & Huntington Cairns (eds.), The Collected Dialogues of Plato, 1018–1085. Bollingen Series, no. 71. New York: Pantheon.
Plato. 1961e. “Theaetetus”, trans. F. M. Cornford. In Edith Hamilton & Huntington Cairns (eds.), The Collected Dialogues of Plato, 845–919. Bollingen Series, no. 71. New York: Pantheon.
Plotinus. 1984a. “On Difficulties About the Soul II”. In Ennead IV, trans. A. H. Armstrong, 136–279. Loeb Classical Library, no. 443. Cambridge, MA: Harvard University Press.
Plotinus. 1984b. “On Intellect, the Forms, and Being”. In Ennead V, trans. A. H. Armstrong, 283–319. Loeb Classical Library, no. 444. Cambridge, MA: Harvard University Press.
Plutarch. 1874. Plutarch’s Morals, ed. William W. Goodwin. Boston: Little, Brown.
Powell, J. G. F. (ed.). 1995. Cicero the Philosopher. Oxford: Oxford University Press.
Proclus. 1970. A Commentary on the First Book of Euclid’s Elements. Trans. Glenn R. Morrow. Princeton, NJ: Princeton University Press.
Rajna, Pio. 1928. “Le Denominazioni Trivium e Quadrivium (con un Singolare Accessorio)”. Studi Medievali 1: 4–36.
Richardson, Ernest Cushing. 1930. Classification: Theoretical and Practical, 3rd ed. New York: H. W. Wilson.
Ritschl, Friedrich. 1877. “De M. Terentii Varronis disciplinarum libris commentarius”. In Opuscula philologica, Vol. 3: Ad litteras latinas spectantia, 352–402. Leipzig: B. G. Teubner.
Robins, R. H. 1957. “Dionysius Thrax and the Western Grammatical Tradition”. Transactions of the Philological Society 56, no. 1: 67–106.
Robinson, T. M. 1979. Contrasting Arguments: An Edition of the Dissoi Logoi. Salem, NH: Ayer.
Rocconi, Eleonora and Tosca A. C. Lynch. 2020. “Introduction”. In Tosca A. C. Lynch & Eleonora Rocconi (eds.), A Companion to Ancient Greek and Roman Music, 1–9. Hoboken, NJ: John Wiley.
Šamurin, Evgenij Ivanovic. 1955. Очерки по истории библиотечно-библиографической классификации, vol. 1. Moscow: All-Union Book Chamber. [Essays on the history of library-bibliographic classification; trans. into German in 1964 as Geschichte der bibliothekarisch-bibliographischen Klassifikation, vol. 1.]
Sandoz, Raphaël. 2018. Interactive Historical Atlas of the Disciplines. Geneva, Switzerland: University of Geneva. http://atlas-disciplines.unige.ch/.
Seneca. 1920. “On Liberal and Vocational Studies”. In Epistles 66–92, trans. Richard M. Gummere, 348–375. Loeb Classical Library, no. 76. Cambridge, MA: Harvard University Press.
Sextus Empiricus. 1935. Against Logicians, trans. R. G. Bury. Loeb Classical Library, no. 291. Cambridge, MA: Harvard University Press.
Shaw, J. Clerk. 2020. “Epicurean Philosophy and Its Parts”. In Kelly Arenson (ed.), The Routledge Handbook of Hellenistic Philosophy, 13–24. New York: Routledge.
Shields, Christopher. 2015. “Aristotle”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/win2016/entries/aristotle/.
Smith, Barry. 2003. “Ontology”. In Luciano Floridi (ed.), Blackwell Guide to the Philosophy of Computing and Information, 155–166. Oxford: Blackwell.
Stahl, William H. 1965. “To a Better Understanding of Martianus Capella”. Speculum 40, no. 1: 102–115.
Stannard, Jerry. 2020. “Pliny the Elder”. In Encyclopædia Britannica. Chicago, IL: Encyclopædia Britannica. https://www.britannica.com/biography/Pliny-the-Elder.
Studtmann, Paul. 2013. “Aristotle’s Categories”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/fall2018/entries/aristotle-categories/.
Sutton, Jane. 2005. “Hippias of Elis”. In Michelle Ballif & Michael G. Moran (eds.), Classical Rhetorics and Rhetoricians: Critical Studies and Sources, 209–213. Westport, CT: Praeger.
Tarán, Leonardo. 1969. “Asclepius of Tralles: Commentary to Nicomachus’ Introduction to Arithmetic”. Transactions of the American Philosophical Society 59, no. 4: 1–89.
Tarán, Leonardo. 1981. Speusippus of Athens: A Critical Study with a Collection of the Related Texts and Commentary. Leiden: Brill.
Tatarkiewicz, Wladyslaw. 1963. “Classification of Arts in Antiquity”. Journal of the History of Ideas 24, no. 2: 231–240.
Tatarkiewicz, Wladyslaw. 1970. “The Aesthetics of the Sophists and of Socrates”. In History of Aesthetics, vol. 1: Ancient Aesthetics, trans. Adam & Ann Cerniawski, ed. J. Harrell, 95–111. The Hague: Mouton.
Taylor, C. C. W., and Mi-Kyoung Lee. 2015. “The Sophists”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/win2016/entries/sophists/.
Taylor, Daniel J. 1974. Declinatio: A Study of the Linguistic Theory of Marcus Terentius Varro. Amsterdam: John Benjamins, 1974.
Tornau, Christian. 2019. “Saint Augustine”. In Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy. Stanford, CA: Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University. https://plato.stanford.edu/archives/spr2020/entries/augustine/.
Verboon, Annemieke R. 2014. “The Medieval Tree of Porphyry: An Organic Structure of Logic”. In Pippa Salonius & Andrea Worm (eds.), The Tree: Symbol, Allegory, and Mnemonic Device in Medieval Art and Thought, 95–116. Turnhout, Belgium: Brepols.
Watson, John Selby. 1891. Quintilian’s Institutes of Oratory; or, Education of an Orator, vol. 1. London: George Bell.
Weisheipl, James A. 1965. “Classification of the Sciences in Medieval Thought”. Mediaeval Studies 27: 54–90. [Reprinted in: Carroll, William E. (ed.). 1985. Nature and Motion in the Middle Ages, 203–237. Washington, DC: Catholic University of America Press.]
West, Andrew Fleming. 1892. “The Seven Liberal Arts”. In Alcuin and the Rise of the Christian Schools, 4–27. New York: Charles Scribner’s Sons.
Whitehead, Alfred North. 1929. Process and Reality: An Essay in Cosmology. New York: Macmillan.
Whitney, Elspeth. 1990. “Liberal and Illiberal Arts: The Classification of Technical Arts in Antiquity”. Transactions of the American Philosophical Society 80, no. 1: 23–55.
Witty, Francis J. 1958. “The Pínakes of Callimachus”. Library Quarterly 28, no. 2: 132–136.
Wolfe, Ethyle R. 1995. “Cicero’s ‘De Oratore’ and the Liberal Arts Tradition in America”. The Classical World 88, no. 6: 459–471.
Zetzel, James E. G. 2018. Critics, compilers, and commentators: An introduction to Roman philology, 200 BCE – 800 CE. New York: Oxford University Press.
Version 1.0 published 2020-09-17
Article category: History of classification and KO
This article (version 1.0) is also published in Knowledge Organization. How to cite it:
Furner, Jonathan. 2021.
“Classification of the scieces in Greco-Roman Antiquity”.
Knowledge Organization 48, no. 7-8: 499-534.
Also available in
ISKO Encyclopedia of Knowledge Organization,
eds. Birger Hjørland and Claudio Gnoli,
https://www.isko.org/cyclo/greco-roman
©2020 ISKO. All rights reserved.