I S K O

Encyclopedia of Knowledge Organization

by Martin Frické

Table of contents:

1. Introduction
2. Boolean logic
3. Some facts or results about Boolean logic
    3.1 The adequacy of the connective set
    3.2 Is the connective set minimal? NAND and NOR
    3.3 Standard equivalences or common theorems
    3.4 Proofs and axioms systems
4. More on using natural language to motivate the properties of the connectives
5. Boolean algebras
6. Some application areas
    6.1 Classification and search: 6.1.1 Venn diagrams; 6.1.2 Regular expressions
    6.2 Faceting
    6.3 Computer programming languages
    6.4 Database queries and query languages
    6.5 Propositional logic
    6.6 Probability theory
    6.7 Switching and computers
7. The shortcomings of Boolean logic for use in knowledge organization
Acknowledgments
References
Colophon

Abstract:
The article describes and explains Boolean logic (or Boolean algebra) in its two principle forms: that of truth-values and the Boolean connectives and, or, and not, and that of set membership and the set operations of intersection, union and complement. The main application areas of Boolean logic to knowledge organization, namely post-coordinate indexing and search, are introduced and discussed. Some wider application areas are briefly mentioned, such as: propositional logic, the Shannon-style approach to electrical switching and logic gates, computer programming languages, probability theory, and database queries. An analysis is offered of shortcomings that Boolean logic has in terms of potential uses in knowledge organization.

[top of entry]

1. Introduction

Boolean logic was proposed by George Boole, principally in two books: The Mathematical Analysis of Logic (1847) and An Investigation of The Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities (1854) (Boole 1847; 1854; Burris 2018). The innovation here was definitive. It represents a step forward and away from Aristotelian logic, which had dominated logic for two thousand years; and it pre-dates and anticipates both modern logic (of which Boolean logic is a part) and abstract algebras (of which Boolean algebra is a part).

The main application areas of ‘Boolean logic’ in knowledge organization are those of post-coordinate indexing and of search. We are all very familiar with back-of-the-book indexes. An index would typically consist of a number of entries; each entry would itself consist of a heading, perhaps with subheadings, and one or more locators (i.e. references, page numbers, URLs, DOIs, ISBNs, etc.); the entries would usually be presented in alphabetical order of headings. In post-coordinate indexing, there might be separate entries with the headings French and cooking, and then a pseudo or virtual entry for the compound heading French cooking would be constructed on demand using as its locators a Boolean and-combination of the locators for French and cooking. The Boolean and-operation here amounts to that of set-intersection between the separate locator sets for French and cooking. A compound heading Benelux royalty might be constructed from (Belgium or Netherlands or Luxembourg) and royalty. The Boolean or-operation is that of set-union between the sets of references. An entry for French non-Provencal cooking might be French and not Provencal and cooking. The Boolean not-operation in this setting is that of set-complement. So, and, or, and not are being used as the glue, or the connectors, to construct the compounds from the atoms or other compounds.

The idea of pre- and post-coordinate indexing comes from Mortimer Taube, in the 1950s (Taube 1951; 1953; Taube and Thompson 1951). But post-coordinate indexing was nearly impossible to do before the advent of computers (simply because, for example, working out the intersection of two or more large finite sets on demand, using just pencil and paper, was not practical). Computers changed the terrain. Finite set operations became trivial. Also, separately, the need for pre-emptively creating index entries, even atomic ones became less pressing. In some cases, the index entries could be produced real time. Computer search, of documents, and wide regions of the Web, became immensely powerful. With many e-books, it is the practice now to omit an index. The reasoning being that the books include computerized full text search which makes an index unnecessary. So, for example, there could be a full text search of ‘French’ and of ‘cooking’ in the blink of an eye, and the results could be combined if need be. (What this reasoning misses, of course, is that at least some sought for terms or potential index entries do not exist verbatim in the text — that might be the case with synonyms — so a full-text search might miss the relevant references. But that is another story.)

This Boolean combination of terms or atoms (or atomic concepts) fits well with faceted classification or faceted search. In mainstream faceted systems, there will be a small number of → facets; for example, the Faceted Application of Subject Terminology (FAST) system uses as facets Topical, Geographic, Form (genre), Chronological, Personal names, Corporate names, Conferences/Meetings, and Uniform titles (Chan and O’Neill 2010; OCLC 2011). For our purposes we can imagine that there are just two facets: place and time. Each facet will have its own set of values (or foci). For example, the place facet might have the values {England, France, Germany, … <and more>}, and the time facet might have the values {16th Century, 17th Century, 18th Century, … <and more>}. The facets are independent of each other . This means that any value from one facet can be combined with any value from another. For example, England can be combined with 17th Century to produce England and 17th Century (or, in real English, 17th Century England). The values within a single facet are usually taken to be dependent, indeed mutually exclusive (Foskett 1977). So, for example, if England is chosen then Germany cannot be chosen at the same time — it is excluded. However, this within-facet-mutual-exclusivity possible requirement does not seem quite right. What essentially is ‘multi-select’ within a facet seems perfectly acceptable (16th or 17th Century seems fine either as part of a heading or as part of a faceted search). At the end of the day, the Boolean operations of and, or, and not, used within and across facets, are useful for faceted classification and faceted search. For example, the Library of Congress Subject Headings (LCSH) is primarily a pre-coordinated system. Yet a 2007 report of theirs writes:

LCSH is a system in which untold numbers of headings can be constructed from individual elements that represent facets, such as topic, place, time, form, and language, and various aspects of topics. Although LCSH is primarily a pre-coordinate system, practice with many complex or multi-element topics requires post-coordination in order to achieve coverage. There are numerous cases in which elements cannot be combined in single headings, even with subdivisions. In those situations, an array of headings may be assigned, that, taken together, are coextensive with the topic of an item.
So, LCSH itself requires some degree of post-coordination of the pre-coordinated strings to bring out specific topics of works. (Library of Congress Subject Headings: Pre- vs. Post-Coordination and Related Issues 2007, 5)

The Medical Subject Heading list (MeSH), largely inspired by Frank Rogers, is another example of a → knowledge organization system which makes use of faceting and post-coordination (Rogers 1953; 1960a; 1960b; Adams 1972; Coletti and Bleich 2001). Rogers was following Taube in emphasizing the construction of complex ideas by conjoining other ideas (Rogers 1960b, 381):

[…] define coordinate indexing as a system of subject cataloging which capitalizes on the concept of the logical conjunction of ideas (the phrase comes from symbolic logic) […]. Taube is simply stressing the fact that complex ideas are often best expressed, or even solely expressed, by the intersection of two or more widely separated ideas, and by the intersection, or conjunction, of their separate word symbols when an attempt is made to catalog those ideas.

We are treating → indexing and → classification as being very similar operations. Indexing produces a data structure which is an association list or a dictionary. It is a structure that links identifiers (or names or headings) with lists (or sets) of values (or locators). These can be inverted so that for any locator the lists (or sets) of headings (or identifiers) that have that value can be produced. Classification is much the same, with one proviso. With subject classification, any book or page or web page may relate to multiple subjects (this is similar to plain indexing). With shelving classification, any book can have only one place in the classification, because it can have only one place on a shelf (this is different to indexing). Usually, there will be hierarchies within the schemes, to permit the movement to and from broader and narrow topics or index entries (or to have books on similar subjects contiguous with each other on shelves). Indexes would also usually be presented in alphabetical order of headings, whereas classification systems might be entirely hierarchical. However, this small potential difference has no significance in the context of Boolean logic.

With subject indexing, to develop an example, the headings (subject identifiers) essentially are tags which are used to tag the references (or locators). The headings themselves will often be from a controlled vocabulary — LCSH and MeSH are — and sometimes those controlled vocabularies will have a grammar that permits the construction of new headings using some Boolean connectives, especially and, either explicitly or implicitly. LCSH, a partially faceted system, allows the attachment of place and time to many headings — this is implicitly to join place and time to the heading using and. The other Boolean connectives or and not are not so often seen in the post-coordinated construction of headings. However, they are common in pre-coordinated components of a controlled vocabularies, and also in settings that do not use a controlled vocabulary at all e.g. in the pervasive free → tagging in social media (e.g. #not-funny), or, separately, in many keyword systems.

Search is similar to and, in many cases, symbiotic with, indexing and classification. Indexing is itself highly non-trivial (see, for example, Vickery 1953; 1975; Weinberg 2009; Wellisch 1991; Zafran 2010; Hjørland 2018). We will assume here that the indexes are available of the requisite quality. Search, in its simplest form, might consist merely of looking through an index in the back of a book. The User in this setting will be trying to make a match, complete or approximate, on available headings (i.e. on the pre-coordinated headings). Computerized search engines can do more. Let us assume that they also can match, completely or approximately, on any pre-coordinated headings in the search system as a whole (the software will use → thesauri and similar devices to be able to do this). Then the French cooking heading mentioned earlier might not even exist as a heading until someone somewhere types into a search engine a string like ‘French and cooking’. Once search creates that heading, it may disappear immediately, it may be cached for one minute, one hour, or for one day, or it may be added sui generis as a heading in its own right. If thousands of Users search for ‘French and cooking’ likely the heading French cooking will be added as a pre-coordinate pre-emptively indexed entry (and cease to be processed in a post-coordinated fashion).

At the core here are manipulations with set-intersection, set-union, and set-complement, and parallel to these are Boolean operations of and, or and not. Of course, ordinary folk are not familiar with set theory and are not going to be able to launch, say, an online search with ‘French set-intersect cooking’. But Boolean operations put a human face on this: ‘French and cooking’.

[top of entry]

2. Boolean logic

Boolean logic is the logic of the truth-values True and False and the three functions not, and, and or. A convenient entry into understanding the syntax and common writing practices of Boolean logic is provided by our experiences with elementary arithmetic and algebra. In such fields, there are expressions like

(3+4) × -(y + z)

In this, there are values (the numbers), there are variables (the y and z), there are two-place functions written infix (the + and ×), there is a one-place function written prefix (the -), the functions are applied to values or variables or a mixture of the two, and there are parentheses to disambiguate expressions. Moving to our main topic, an example expression in Boolean logic is

(True ∨ False) & ~(P ∨ Q)

There is the same mix here of values, variables, infix and prefix functions, and parentheses. In mathematics and computer science, functions that are written infix (i.e. between their arguments) are often called ‘operators’. In straight out logic or philosophy, Boolean functions are often called ‘connectives’. So, ‘Boolean functions’, ‘Boolean operators’, and ‘Boolean connectives’ are more-or-less synonyms.

In Boolean logic, True and False are often abbreviated T and F (and, in some settings, 1 and 0). It is common to use symbols to represent the connectives, but, unfortunately, there is no complete standardization and there is a variation in the symbols that might be used. Here are some choices that might be encountered:

not : ~ (symbol name: 'tilde')
        ¬ (symbol name: ‘not’)
and : ∧ (symbol name: ‘and’)
         & (symbol name: ‘ampersand’)
         . (symbol name: ‘period’)
or :   ∨ (symbol name: ‘vel’)
        + (symbol name: ‘plus’)

Then formulas are constructed using these symbols, and sometimes parentheses also to resolve ambiguities. Here are some examples:

True
False
~ True
False & True
~ False ∧ True
~(False & True)
True + ~ False
True & (False ∨ ¬ False)

As illustrated in the earlier example above, there are often also variables. Quite what would be used as variables depends on the context and application, but upper-case letters would be common e.g. P, Q, R, …

The connective not applies to just one argument, and it is written prefix (i.e. before the formula it applies to). The connectives and and or apply to two arguments, and they are written infix (i.e. between the arguments they apply to). The arguments, or components, can be atomic formulas, but they can also be compound formulas. The usual practice, and it is a prudent one, is to use parentheses liberally. Not i.e. ~ is applied to the formula immediately following it (it is the connective with highest precedence). Parentheses are not necessary for this, but they can be used optionally. But with formulas with several ands and ors parentheses are pretty much a necessity. Some writers give and a higher ‘precedence’ than or. This would mean that a formula like

True & False ∨ True

(True & False) ∨ True

True & (False ∨ True)

However, assigning precedence to and and or is by no means universal — it is not even common. Ergo, parentheses should be used in complex formulas.

True and False — the truth values — are the core of Boolean logic. However, Boolean logic applies in many areas. That is, its inherent ‘logic’ applies widely. One central example, useful for illustration, concerns propositional logic, an elementary form of reasoning using propositions. Indicative sentences in a natural language, English, for instance, are either true or false. For example, ‘The Eiffel Tower is in Paris.' is an indicative sentence (which happens to be true). Such sentences express statements or propositions. Not all pieces of language express propositions. For example, the question 'What day is it today?' is not either true or false (although reasonable answers to it will be either true or false); again, the greeting 'Have a nice day!' is not either true or false. Statements or propositions or sentences can be atomic or compound. ‘The Eiffel Tower is in Paris.’ expresses an atomic proposition; whereas ‘The Eiffel Tower is in Paris and the Eiffel Tower is 25 kilometers from the nearest ocean.' expresses a compound proposition composed of two atomic propositions (one true one and one false one). There are many ways to construct compound propositions from atomic propositions and other compound propositions, but propositional logic focusses on five connectives only: ‘not’, ‘and’, ‘or’, ‘if…then’, and ‘if and only if’. There is a larger set of connectives here than is in use in basic Boolean logic, but it turns out that Boolean logic can model propositional logic very well.

In propositional logic, propositions, statements, or indicative sentences are the ‘bearers’ of truth i.e. each of them has a truth value of either True or False. We will not be looking here at what conditions are required for a proposition to be true — we will just take it that each of the propositions either is true or is false. For example, we take it that the proposition ‘The Eiffel Tower is in Paris' either is true or is false. Notice here that from the point of view of logic we are not concerned whether anyone knows it to be true or knows it to be false, or believes it to be true, or believes it to be false. We just want there to be the two possibilities — that it is true, that it is false — and that the proposition is one of them. Then, in a particular context, instead of writing out the sentences or propositions in natural language, perhaps several times over, propositional variables, perhaps P, Q, R … are used to stand for the propositions. The results are examples like

~P (in English, ‘not-P’)
P & Q (in English, ‘P and Q’)
~R ∨ Q (in English, ‘not-R or Q’)

Propositional variables stand for propositions, atomic or compound. So, it would be possible to use P to stand for the atomic ‘The Eiffel Tower is in Paris' or, alternatively, for the compound ‘The Eiffel Tower is in Paris and the Eiffel Tower is 25 kilometers from the nearest ocean.' However, it would be unusual and idiosyncratic to adopt the second alternative. The heuristic reason being: it wise to analyze with the finest granularity available so as to reveal logical structure. The second alternative ignores the Boolean connective ‘and’ and that would not be good.

There is an assumption about the atomic truth bearers. It is that they are independent. This means that all combinations of truth values are possible. So, for example, if P and Q are atomic propositions then it must be possible for P to be true while Q is also true, P true while Q is false, P false while Q is true and P false while Q false. As an example where independence is violated, consider the propositions ‘All swans are white’, P say, and ‘All swans in New Zealand are white’, Q say; in this case, it is not possible for P to be true and Q false; P and Q are not independent and are thus not suitable as atomic truth bearers.

The connectives are functions. They take as input, or arguments, the truth values of their components, and they have as output, or value, exactly one of the truth values True or False. The behavior of the connectives can be laid out in truth-tables. These describe the function values for the different function arguments. To assist with this, we will use A, B, C, etc. as variables to stand for entire formulas in the Boolean logic.

Consider a formula with the form ~A. If the formula A is true, then the compound formula ~A is false. If the formula A is false, then the compound formula ~A is true. Summing this up in a table:

Table 1: Truth-table for ~
 

A	~A
True	False
False	True

Similar considerations apply to the other connectives. If A is true and B is true, then (A&B) is true. If A is true and B is false, then (A&B) is false. If A is false and B is true, then (A&B) is false. If A is false and B is false, then (A&B) is false. Summing this up in a table:

Table 2: Truth-table for &
 

A	B	A&B
True	True	True
True	False	False
False	True	False
False	False	False

If A is true and B is true, then (A∨B) is true. If A is true and B is false, then (A∨B) is true. If A is false and B is true, then (A∨B) is true. If A is false and B is false, then (A∨B) is false. Summing this up in a table:

Table 3: Truth-table for ∨
 

A	B	A∨B
True	True	True
True	False	True
False	True	True
False	False	False

Our interest is with Boolean logic itself so we will omit truth-tables for if… then and if and only if.

The truth value of compound formulas, or propositions, is fixed entirely by the truth value of their (immediate) constituents; and the truth value of the constitutions is fixed by the truth value of their constituents, and so on, decomposing down to atomic formulas or propositions.

In a standard truth-table for an expression, there are columns for each atomic formula in the expression, and a column for the expression itself. So, for example, if the expression has three different atomic formulas in it, there will be four columns. Each row is a different combination of truth-values for the atomic formulas. So, an expression with three atomic formulas will have eight rows. (Sometimes truth-tables will contain extra columns for non-atomic subexpressions of an expression. This is just to facilitate the evaluation of the formulas.)

Truth-tables extend to more complicated cases. We just work our way out from the atomic formulas to the ever more complex compound formulas. Consider the formula ~(~(~A)). There are two possibilities for A itself, that it is true, and that it is false. Let us follow them through in turn. If A is true, ~(~(~A)) amounts to ~(~(~True)) which amounts to ~(~(False)) which amounts to ~(True) which amounts to False. If A is false, ~(~(~A)) amounts to ~(~(~False)) which amounts to ~(~(True)) which amounts to ~(False) which amounts to True. Summing this up in a table:

Table 4: Truth-table for ~~~A
 

A	~A	~~A	~~~A
True	False	True	False
False	True	False	True

[top of entry]

3. Some facts or results about Boolean logic

3.1 The adequacy of the connective set

Boolean formulas are functions from the truth-values of their (atomic) constituents to the truth-values {True, False}. A question is: are the formulas, in particular their connective set {~, &, ∨}, rich enough to be able to portray all such functions? They are indeed, and this can be proved by conjunctive normal forms. (As a matter of terminology: formulas with main connective and are often called ‘conjuncts’, and formulas with main connective or are often called ‘disjuncts’.)

To focus our thinking, consider how many such functions there are. Suppose there were three atomic constituents A, B, C, and each of these might have the values True or False, then there would be eight lines or rows in an individual truth-table; for each of these lines or combinations a function itself might have the value True or False; so there are 2⁸ = 256 different functions. More generally, for n atomic constituents there are 2^r functions, where r = 2ⁿ.

We can construct a formula for any of these functions as follows. Define a literal to be either A or ~A, where A is atomic. (Note that a literal is False either if it has the form A and A is False, or if it has the form ~A and A is True.) Then define a clause to be a disjunct of literals. So, for example, a clause might be

(A ∨ ~B ∨ C)

Notice that a clause is False only if all of the literals in it are themselves False, otherwise the clause will be True. Finally, a formula is in conjunctive normal form if it is a conjunct of clauses. So, for example,

(A ∨ ~B ∨ C) & (~A ∨ B ∨ C)

Now, a disjunct, or clause, is False only if all of its literals are False. So, for example, (A ∨ ~B ∨ C) is False only if A is False and B is True and C is False. Then a conjunct of clauses is False only if at least one of its clauses is False. So, for example, (A ∨ ~B ∨ C) & (~A ∨ B ∨ C) is False only if either (A ∨ ~B ∨ C) is False or (~A ∨ B ∨ C).

This allows us to produce from any truth-function a formula that represents it. We do that by direct construction from the ‘False’ lines. To give an example. Consider the function

Table 5: Table for an example truth-function
 

A	B	C	?
True	True	True	False	1
True	True	False	True	2
True	False	True	True	3
True	False	False	True	4
False	True	True	True	5
False	True	False	True	6
False	False	True	False	7
False	False	False	True	8

When constructing, our interest is only in the lines which have the value False, namely lines 1 and 7. The clause

(~A ∨ ~B ∨ ~C)

(A ∨ B ∨ ~C)

(~A ∨ ~B ∨ ~C) & (A ∨ B ∨ ~C)

Some functions do not have any False lines at all in their truth-tables. Every line has the value True. A conjunctive normal form for such functions can be produced merely by putting the two different literals of the same atomic variable into a single clause (no conjunctions needed) e.g.

(A ∨ ~A)

This construction technique is completely general. This means that all truth functions can be represented as formulas in Boolean logic.

[top of entry]

3.2 Is the connective set minimal? NAND and NOR

Formulas using {~, &, ∨} are rich enough to represent any Boolean truth-function. But might a smaller number of connectives be able to do the same job? The answer to that is that it can be done even by a single connective, and there are two such single connectives that can do it: NAND and NOR. This was discovered by Charles Peirce and Henry Sheffer, about the beginning of the 19th century. Roughly, NAND amounts to and with a negation in front of it, and NOR amounts to or with a negation in front of it. NAND, &, has the truth-table

Table 6: Truth-table for A&B
 

A	B	A&B
True	True	False
True	False	True
False	True	True
False	False	True

Then our original Boolean connectives not, and, and or can be define in terms of this. For example, ~A amounts to A&A i.e. A NAND A.

Table 7: The NAND counterpart of ~A
 

A	A	A&A	~A
True	True	False	False
False	False	True	True

NAND (and NOR) do not lend themselves to intuitive reasoning in the same way that not, and and or do. However, they are extremely important. Boolean logic has become the basis of modern digital computers and the fact that one style of fabrication of transistors (say, for a NAND gate) could do everything effected a great simplification.

[top of entry]

3.3 Standard equivalences or common theorems

Some formulas are logical truths; that is, they evaluate to true no matter what the truth values of their constituents. Most prominent among these is:

A ∨ ~A      The law of excluded middle

The Aristotelian law of excluded middle or Tertium non datur (the third is not given) means that every proposition either is true or is false. This law or principle is part of Boolean logic (but it is not uncontroversial in a wider setting; for example, it is denied by intuitionistic propositional logic). Then there is Aristotle’s law of non-contradiction:

~(A & ~A)      The law of non-contradiction

Some formulas are logical falsehoods; that is, they evaluate to false no matter what the truth values of their constituents. A plain contradiction:

A & ~A

Some pairs of formulas are logically equivalent to other; that is, the truth-table for one of them is identical to the truth-table for the other. We can use the triple-bar symbol ≡ to indicate equivalence. Here are some important equivalences:

A & True ≡ A      Identity for &
True & A ≡ A      Identity for &

A ∨ False ≡ A      Identity for ∨
False ∨ A ≡ A      Identity for ∨

A ≡ ~~A      Double negation

A & ~A ≡ False     Complement for &
A ∨ ~A ≡ True      Complement for ∨

A ≡ A & A      Idempotence for &
A ≡ A ∨ A      Idempotence for ∨

A & B ≡ B & A      Commutativity of &
A ∨ B ≡ B ∨ A      Commutativity of ∨

A & (B & C) ≡ (A & B) & C      Associativity of &
A ∨ (B ∨ C) ≡ (A ∨ B) ∨ C      Associativity of ∨

A & (B ∨ C) ≡ (A & B) ∨ (A & C)      Distributivity of & over ∨
A ∨ (B & C) ≡ (A ∨ B) & (A ∨ C)      Distributivity of ∨ over &

~(A & B) ≡ ~A ∨ ~B      De Morgan law 1
~(A ∨ B) ≡ ~A & ~B      De Morgan law 2

These equivalences can be proved using many different proof techniques. But truth-tables themselves bear witness to their soundness. For example, here is a truth-table for the left-hand side of De Morgan law 1 (including values for the sub-expressions to show how the evaluation is carried out):

Table 8: Truth-table for L.H.S. of De Morgan law 1
 

A	B	A&B	~(A&B)
True	True	True	False
True	False	False	True
False	True	False	True
False	False	False	True

And here is a truth-table for the right-hand side of De Morgan Law 1

Table 9: Truth-table for R.H.S. of De Morgan law 1
 

A	B	~A	~B	~A ∨ ~B
True	True	False	False	False
True	False	False	True	True
False	True	True	False	True
False	False	True	True	True

The truth-table values for ~(A&B) and ~A ∨ ~B are the same, which means that the expressions or formulas are equivalent.

[top of entry]

3.4 Proofs and axioms systems

Some arguments, using truth-tables, were given above for the soundness or logical truth of various equivalences. Alternatively, some formulas, either from these equivalences or from other formulas, could be adopted as ‘axioms’ and various theorems proved from them. For example, the commutativity of & could be taken as an axiom i.e.

A & B ≡ B & A

(A & B) & (C & D) ≡ (D & C) & (B & A)

These questions have been studied, especially the question of what is the absolute minimum. Within this realm it is often usual to use only the NAND connective i.e. &. This gives a convenient count in as much as the axioms can be counted, and the NANDs can be counted. Henry Sheffer produced a 3 axiom system in 1913; in 1967, Carew Meredith proposed his final 2 axiom system. Then, in 2000, Stephen Wolfram discovered a single axiom solution (Wolfram 2018):

((A & B) & C) & (A & ((A & C) & A)) ≡ C    One single axiom for Boolean logic

There is here one axiom with 6 NANDs. Wolfram asserts ‘this one little axiom was enough to generate all of logic’. Well, perhaps more accurately, it is enough to generate all of Boolean logic. We can get all of Boolean logic from this by simple algebraic transformations.

[top of entry]

4. More on using natural language to motivate the properties of the connectives

While the and, or, and not of Boolean logic are similar to central use cases of and, or, and not in natural language, they are not exactly the same. For example, the and in natural language can often have a temporal element in it. ‘He fell off his bike and he went to hospital’ is not the same as ‘He went to hospital and he fell off his bike.’. This means that the ‘and’ in natural language is often not commutative (as it is in Boolean logic).

The or in natural language really has two senses: inclusive-or and exclusive-or. The first means one-or-the-other-or-both and the second means one-or-the-other-and-not-both. An example of the first is ‘(From the wild celebrations we can tell that) Jane passed the exam or Jim passed the exam.’; an example of the second is ‘The getaway car took the left fork in the road or the getaway car took the right fork in the road.’ Latin has separate words for these connectives ‘vel’, for the inclusive-or, and ‘aut’, for the exclusive-or. Boolean logic, plain and simple, uses the inclusive-or. However, in computer science and electrical engineering there is application for the exclusive-or. In those contexts, often an exclusive-or connective, XOR, or ⊕, will be defined with the truth-table

Table 10: Truth-table for XOR
 

A	B	A⊕B
True	True	False
True	False	True
False	True	True
False	False	False

XOR is not something new in as much as it can be defined as (A ∨ B) & ~(A & B).

In sum, many of the laws or equivalences of Boolean logic do not hold universally in natural language. One consequence of this is that Boolean searches using a search engine need some care. Of course, the underlying software to a search engine will have some sophisticated algorithms and tuning to ferret out what the searchers might mean as opposed to what they actually say in terms of Boolean logic.

[top of entry]

5. Boolean algebras

The structure of the expressions in Boolean logic form an algebra, in the sense of abstract algebras. This means that their structure can be studied as an advanced mathematic topic, in a similar way to the study of algebraic structures like groups, rings, modules, vector spaces, lattices, or fields. It would be usual in these settings to drop the use of True and False and use 1 and 0 instead. Then some of the equivalences above (identity, commutativity, associativity, and distributivity) can be used as axioms to define an algebra, namely: Boolean algebra. There are many examples of Boolean algebras in abstract mathematics (the algebra of sets, mentioned above, with set-intersection, set-union, etc. is one). There are some profound theorems about Boolean algebras; the Stone representation theorem is one example (Stone 1936).

[top of entry]

6. Some application areas

6.1 Classification and search

6.1.1 Venn diagrams

As explained above, Boolean connectives are often used in knowledge organization as a front-end to set theoretic operations. Also useful in this context are the familiar Venn diagrams (Bednarek 1970). These can be used to illustrate set-complement, set-intersection, and set-union.

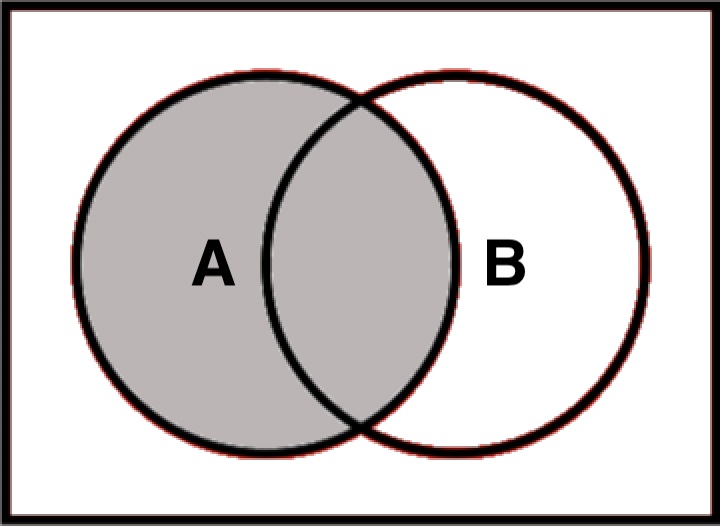
The rectangle as a whole represents the Universe. The circle labeled ‘A’ represents the set of As (i.e. the set of those items in the Universe that have the property A). Outside the circle, i.e. outside the shaded area, but inside the rectangle, represents the complement, or complement set, of A i.e. ~A. The conventions are similar for B: the circle labeled ‘B’ represents the set of Bs. The common intersection area represents those items which are both A and B i.e. A & B. The contents inside either of the two circles represents the union of A and B i.e. A ∨ B. There is also the notion of relative complement, which are items in one set but not the other e.g. A & ~B. In sum, diagrams like the following may be used to depict the relevant areas:

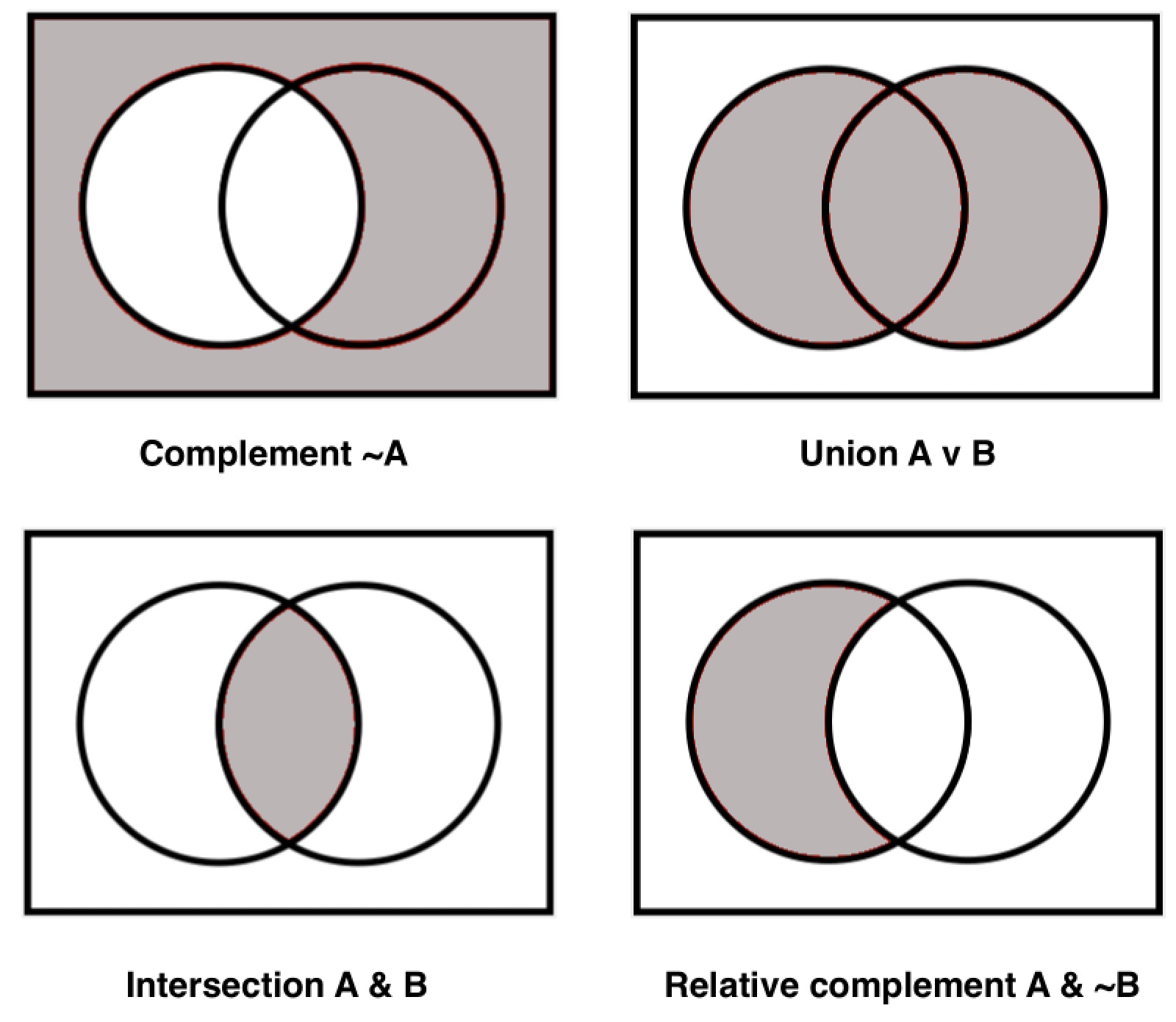
This schematic can be extended to three or more sets (i.e. to three or more circles or elliptic boundaries).

There is an important point of interpretation here. In Boolean logic, the values are True and False and a formula like P & Q denotes, say, True & False which, in this case, would have the value False. In a Venn diagram, the circles represent sets. The As and Bs represent properties which may or may not be possessed by items in the set universe as a whole. For example, consider the universe of people. There are the properties A = ‘x is agreeable’ and B = ‘x is benevolent’. Then, the circle labeled A can be used to depict the people that are agreeable, and outside the circle A depicts the people that are not agreeable. A similar convention can be used for B. Then the intersection area labeled ‘A & B’ represents the people who are both agreeable and benevolent. So, the actual formula A&B is not a formula of Boolean logic, rather it is the anding of two properties. This can be done formally in predicate logic, but not in propositional logic or Boolean logic. In set theory, there is the axiom or principle of comprehension which states that a property, atomic or compound, can be used to define a set. That is what is happening here. Naïve set theory has a ‘set-builder’ notation, usually

{x: Φ(x)} or
{x| Φ(x)}

 A = {x: A(x)}
-A = {x: ~A(x)}                 complement
A ∩ B = {x: A(x) & B(x)}  intersection
A ⋃ B = {x: A(x) ∨ B(x)}  union

There is also the characteristic function which can be used to produce True or False statements from set membership or the application of properties. Without going into any more detail, Venn diagrams and Boolean logic can be used to mimic parts of each other. When post-coordination, or search, puts together the terms French and cooking to produce French and cooking i.e. French cooking, really it is doing set operations rather than strict Boolean logic operations.

It is fairly standard, and mainstream, to maintain that there are at least two prototypical examples of Boolean logic or Boolean algebra. The first uses the truth-functional operations of and, or, and not, together with the truth values True and False; and the second uses the set-theoretic operations of intersection, union, and complement, together with the Universe set and the Null set.

In the case of knowledge organization, the universe of discourse for Venn diagrams, or the set-theoretic operations, is that of references or identifiers or locators such as ISBNs of books, page numbers, URLs, DOIs, etc.

[top of entry]

6.1.2 Regular expressions

There is more that can be said about search and Boolean logic. One question that arises in a search framework is what is desirable as the form of the input for a search? An initial thought is that it should be a single word, or expression, say ‘house’ or a Boolean combination of single words, say ‘house or apartment’. This overlays Venn diagrams neatly. A search for ‘house or apartment’ produces the locators for ‘house’ and the locators for ‘apartment’ and adds the two locator sets together i.e. it uses their union. Other cases will be similar.

But then everyone with some familiarity of knowledge organization, indexing, and thesaurus construction will be aware of stemming, wild cards, and other manipulations. It is possible for a search, with a single atomic input, to retrieve locators for {house, houses, housing, farmhouse, lighthouse, farmhouses, lighthouses, etc.} (see, for example, Stock and Stock 2013a). Now the input form is going to be a pattern (which perhaps might be a literal). The next step is to be aware of regular expressions (Goyvaerts 2020) and text search algorithms. Regular expressions (regexs) come from the logician Stephen Kleene, and they were brought into Unix and computer programs by Ken Thompson (Kleene 1956; Thompson 1968). More-or-less every modern text search algorithm by computer is going to use regular expressions as its input. To give an example

[A-Za-z]*(House|house)[a-z]*

/[A-Za-z]*(House|house)[a-z]*/g

This means that behind the scenes, with programmers and text processing experts, there is no such thing as Boolean search. With everyday folk, it is a different story, although Boolean search is very hard to do competently. In sum, Boolean search is for experts, but experts rarely, if ever, use it. Experts would use some variation of the more powerful regex search.

A plain Boolean search is not going to be able to retrieve the collective locators for {house, houses, housing, farmhouse, lighthouse, farmhouses, lighthouses, etc.}. It is true that a Boolean search for ‘house or houses or housing or farmhouse or lighthouse or farmhouses or lighthouses’ should return a set of locators. However, this type of search, and its success, is limited to what the User or searcher can envisage when launching the search. Imagine that the user never even thought of ‘outhouses’ as a possibility. If that literal were not among the Boolean input, its locators would not be retrieved. But the corresponding regex search would capture locators for ‘outhouses’.

We should perhaps be a little more sensitive to the scale of the expertise of the searcher. It is not the case that there are just experts and beginners. There are shades of grey in between. Correspondingly, a search engine might have ordinary search, allowing Boolean search, but perhaps not much more. Then it might have ‘Advanced search’ perhaps exposing wildcards etc. as a human friendly interface to parts of regex search. Then it might even allow full-blown regex search.

Another consideration here is how the text is processed or indexed in the first place. Regex search processes explicit text. It can do that real time, or it can do it in advance preemptively to produce an index. To a limited degree it can deal with challenges like synonyms, if the programmers are smart. For example, it can be set up to retrieve locators for the concept ‘automobile’ where the text does not have instances of that word at all but instead has occurrences of the word ‘car’. But human indexers can improve on computers and regex searches in challenging cases. The human indexers understand the text and this, for example, might allow them to say that an entire book is on unrequited love. Regex search would fail at this, if ‘unrequited love’, or its synonyms, did not appear explicitly in the text.

Plenty of material is indexed by humans. The Library of Congress Subject Headings (LCSH) are attached to most print books by humans. The Medical Subject Headings (MESH) are also assigned by humans. There are many more examples. In these areas, pure Boolean search makes something of a comeback intellectually. In essence, the searches are for those items tagged with heading1 or those items tagged with (heading1 or heading2), etc. Regex search can be used here also. For example, a regex input can easily search through 300,000 or so LCSH headings and find all the locators, maybe books, within a particular library’s collection. But LCSH is a controlled vocabulary, and a good librarian will know most of what is there, i.e. most of the headings, verbatim. So, a good librarian will be able search effectively in settings like these using just Boolean search.

In sum, where there is search or indexing of large quantities of free text, where the focus tends to be on the explicit, and the searchers are experts, likely there will be regex search and little use for Boolean operators. In cases where humans have intermediated and added value to the indexing or classification, and the searchers either are experts on the indexing or at least understand Boolean search, likely Boolean search will still have a role.

[top of entry]

6.2 Faceting

There is insight to be gained by looking at faceting in terms of, on the one hand, the headings or search strings it permits, and, on the other, the sets of locators that it produces and their interactions. Almost all traditional classification systems that have faceting (e.g. LCSH, MeSH, → Colon, Universal Decimal Classification (UDC), Art and Architecture Thesaurus (AAT), etc.) use controlled vocabularies with a defining grammar (Library of Congress Subject Headings 2020; MeSH 2010; Ranganathan 1952; McIlwaine 1997; Whitehead 1989). They do use, for example, and, between foci across facets. (This use may be implicit, of course.) Earlier, in the Introduction, we saw the imagined example of an England focus being combined with a 17th Century focus to produce the composite 17th Century England. But real cases of classification systems (LCSH, MeSH, etc.) will often have a grammar that prevents these cross-facet uses from being commutative. For example, the grammar may permit a heading with <place> and <time> in that order, but then not a similar heading with <time> and <place> in that order. Also, as mentioned, or would be pretty rare across facets, as would not. In sum, it is a bit of a stretch to assert that familiar controlled vocabulary headings, with facets, permit the construction of new headings using Boolean logic. In contrast, if the headings are not from a controlled vocabulary — as might be the case with social media tagging — anything goes. Search strings, offered as input to a normal search engine, would usually be allowed to have any form (any vocabulary, any grammar, and, sometimes, even in many different natural languages). Most modern search engines would also accept a composite of component strings appended together by Boolean connectives (mostly with full commutativity, distributivity etc.). They also would be able to take the components sequentially to narrow or broaden on the results obtained to that point — making a search into a process with feedback. This is important, especially for search by experts (Hjørland 2015). Search engines, as described, do use something akin to Boolean logic on the search strings. Faceting is not much in evidence here (after all, the user has much freedom with the search strings and is not constrained by faceting).

However, many web sites, for example, for online retailers, like Amazon, do provide faceted search for their goods and services. For example, the user may search under a facet of ‘gifts’ (and be offered a menu choice among such foci as wedding gifts, birthday gifts, xmas gifts etc.) and combine this with a menu choice from a facet of ‘price’ (and be offered inexpensive, moderate cost, expensive, etc.). This kind of faceted search for goods and services does have the characteristics of a Boolean logic. Whether the topic of faceted search for goods and services is properly a part of the discipline of knowledge organization is an open question. It can be remarked, though, that the much-admired Art and Architecture Thesaurus covers much more than locators or references. It covers ‘art, architecture, and material culture’ i.e. it includes goods and services.

Also, many modern online public access catalogs (OPACs) offer faceted search; for example, WorldCat, the world’s largest catalog, does (WorldCat.Org 2020). Systems like these often offer narrowing by choice of facet (e.g. keyword, subject, title, author, year, audience, etc.). Some of the facets, such as keyword, subject, and title, accept free-text; others require a choice among fixed values (with WorldCat, the facet ‘Content’ requires a choice of a single focus from {Fiction, Non-fiction, Biography, Thesis/dissertation}). Typically, what is happening here is that there are extensive bibliographical records in the background (WorldCat has access to 2 billion records). Then these records have extensive metadata fields (e.g. author, subject, title, ISBN, accession number, etc.) What a faceted search interface does is to allow access to these metadata fields in a semi-structured and rational way. Before the widespread use of computers in libraries, there would have been card catalogs perhaps with separate ‘entry points’ to provide access and search by author, title, and subject. But computers have the potential to offer as an entry point any field that is among the metadata. Some OPACs may accept and process Boolean operations within a facet (e.g. author: Dickens or Austen); practices on this are unclear and probably not uniform. The systems often take free text, so ‘author: Dickens or Austen’ would be accepted as input; but what processing would be done, and what the output would be, would likely vary from system to system.

The interactions of sets of locators produced by faceted, or indeed, by plain Boolean search, is as has been described earlier. Providing the sets come from the same underlying Universe (in this case locators), then set-intersection, set-union, and set-complement are sufficient. However, if faceted classification, in combination with Boolean logic, is going to be used with ‘goods and services’ issues arise. Imagine that a web site sells socks. It sells long socks and short socks, and cotton socks and wool socks. The set-theoretic Universe here is well-defined (i.e. socks), as are the various subsets and set-operations, and a search, for example, for ‘long, and not cotton’ is perfectly sound in terms of Boolean logic. But most classification theorists want to go a lot further with their faceting than this. Julius Kaiser, to use a historical example, wanted to have the kind (i.e. facet) ‘concretes’ and the kind ‘processes’ and to combine these to form, for example, ‘the rusting of iron’ (i.e. iron and rusting) (Kaiser 1911). Something very different is going on here. No doubt Kaiser himself had his eye on locators. So, roughly speaking, he would form an index heading for ‘the rusting of iron’ and expect that the locators (i.e. page numbers) for that heading within a given book would approximate the intersection of the set of locators for iron and the set of locators for rusting. This is absolutely fine. But it does not work so well if taken away from locators into the actual world of things and processes. Suppose a modern-day Kaiser left librarianship, opened a foundry, and started selling the concrete iron and, additionally, services including processes like smelting. A universe that includes both concretes and processes has items of different kinds. Then a label like ‘the smelting of iron’ does not seem to denote the set-theoretic intersection of iron and smelting. Any intersection of two sets is also subset of the two sets individually (in the Venn diagram above A&B is a subset of A and a subset of B). This would mean that ‘the smelting of iron’ is a member of the concretes. The original Kaiser surely would not have said that.

[top of entry]

6.3 Computer programming languages

Almost all computer programming languages have Booleans i.e. {True, False} as a datatype. Then Boolean operators are often used in expressions or in control statements. For example, using an imaginary programming language schematic:

If ((not password has at least six characters) or
    (not passwords uses at least one special character) or
    (not (password has one upper case character and
         password has one lower case character)) or
    (not password has a numeric character))
then
    writeln ‘Passwords need to be at least six characters long and include upper and lower case characters, a special character, and a numeric character.’

[top of entry]

6.4 Database queries and query languages

Many databases expose their data to searchers at large. Then, often, a search query would be able to use the Boolean operators of and, or and not. The resulting query language would amount to a formal or semi-formal Boolean query language. The PubMed database is an example of this (PubMed 2020). This use is similar to online search using a search engine in a web browser. It is not exactly the same because ordinary folk use web browsers, and they may struggle with Boolean operators. Whereas Users querying databases using query languages usually have some expertise and will be comfortable with Boolean operators. This difference between ordinary folk and expert searchers has some significance. For example, Hjørland argues powerfully that experts using Boolean searches are the match of any other technique, if not actually superior to other techniques; this would not be true of neophytes (Hjørland 2015; Hearst 2011).

[top of entry]

6.5 Propositional logic

This application area has been described in section 2.

[top of entry]

6.6 Probability theory

Boolean logic is central to probability theory. It is possible to set up probability theory either in terms of true or false propositions or in terms of sets of events and their unions, intersections etc. (Howson and Urbach 1993). Either way Boolean logic is right at the heart of it (Hailperin 1986). This reliance on Boolean logic in probability theory can be traced back to Boole himself. Theodore Hailperin writes (Hailperin 1984, 199):

Boole, more than anyone before him, realized and exploited the close relationship between the logic of not, and, and or and the formal properties of probability. He forced this relationship to be closer than it really is by restricting himself to or in the exclusive sense (so that probabilities of an or-compound added) and by believing that all events were expressible ultimately in terms of independent events (so that the probabilities of an and-compound multiplied) […]. Boole believed […] that he had solved the central problem [of probability theory.]

Plenty of work has been done on probability since Boole’s time, but certainly Boolean logic still has a major role in the field.

[top of entry]

6.7 Switching and computers

In 1938, Claude Shannon made extensive using of ‘switching algebra’ in his analysis of electric circuits (Shannon 1938). This was part of his Master of Science degree. Switching algebra was basically Boolean algebra. Shannon writes (p. 2):

This calculus is shown to be exactly analogous to the Calculus of Propositions used in the symbolic study of logic.

We are now in a position to demonstrate the equivalence of this calculus with certain elementary parts of the calculus of propositions. The algebra of logic […] originated by George Boole, is a symbolic method of investigating logical relationships.

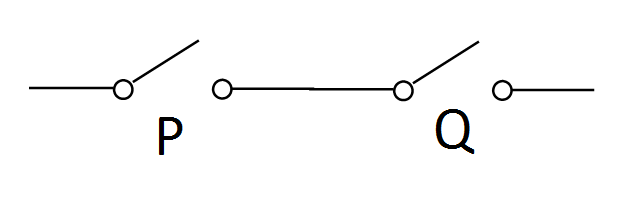
The core ideas are fairly simple. Two switches in series will light a lamp, or allow electricity to flow, if and only if both are switched on (i.e. and).

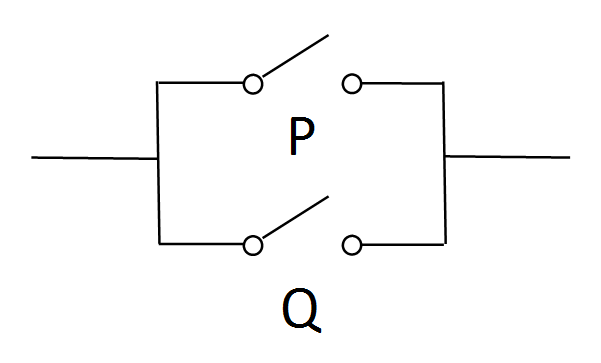
Two switches in parallel will allow electricity to flow if and only if at least one of them switched on (i.e. or).

Producing a schematic for not is a little more challenging. An easy way is just to posit a not switch, which when the switch is ‘on’ no current flows and when the switch is ‘off’ current actually does flow. (Those of a Rube Goldberg turn of mind can produce a negation switch as follows. There is an electromagnet which when ‘on’ holds another switch open (by magnetism), then, when the electromagnet is ‘off’ the other switch is closed by a spring (there is no magnetic force holding it open). The result is, when the electromagnetic is on, the other switch is off, and when the electromagnetic is off, the other switch is on — that is negation or not.)

Then these ‘switches’ can be wired together to produce an instantiation of any Boolean formula or combination e.g. P&Q&~R. For more detail, please see Enderton (2001, 54-ff.)

This starts to become very important with arrival of computers and the use of binary (i.e. 0 and 1) to represent numbers (and then from numbers to everything else that could be represented in digital e.g. text, images, videos, film etc.). So-called ‘logic gates’ for and, or, nand, nor, etc. were devised to implement the Boolean Operations e.g. the XOR-gate (Figure 5).

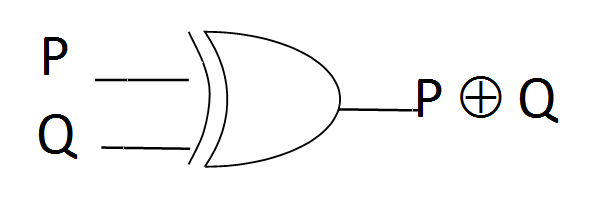
To give an example of how this works. The addition of two single binary digits is as follows:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0 (carry 1)

Table 11: Truth-table for XOR
 

A	B	A⊕B
True	True	False
True	False	True
False	True	True
False	False	False

It is but a short step from there to computers being ruled by Boolean logic (or Boolean algebra). We should perhaps acknowledge that a modern computer might have a billion, or more, logic gates in it. There is a little more to computers than one or two truth-tables.

[top of entry]

7. The shortcomings of Boolean logic for use in knowledge organization

Boolean logic is not strong enough for every potential use in knowledge organization.

In post-coordination, there are the familiar examples of the pairs ‘Venetian blind’ and ‘blind Venetian’, and ‘school library’ and ‘library school’. So, for example, if school and library are headings for pre-coordinated index entries, then either of ‘school library’ or ‘library school’, assembled post-coordinately, are going to produce many false positives. The problem here is that words like ‘blind’, ‘library’, ‘school’ and ‘Venetian’ are each individually both nouns and adjectives and can be assembled in different ways. Essentially, ‘library’, for example, is a homograph of itself. Problems like these can be partially resolved by paying attention either to word order and proximity, or to the grammar and grammatical parts of speech. But Boolean logic on its own cannot solve this. Also, as alluded to earlier, the match between natural language and the Boolean connectives can be loose. As another example, if we invite friends and colleagues to our party, we would usually be inviting friends or colleagues (not just those individual folk who are both friends and colleagues i.e. in the intersection area of a Venn diagram) — so and means or in cases like these. There is evidence that ordinary Users basically do not understand Boolean operations in the context of search (e.g. they think that a search for ‘cats and dogs’ will produce locators for cats together with locators for dogs (i.e. set-union not set-intersection)) (Hearst 2011). Also, Users simply do not use Boolean operations in their searches (except and very occasionally) (Lowe et al. 2018). Most university libraries offer incoming freshmen instruction in Boolean search, as part of preparation for college life. But, really, once you have to instruct intelligent people how to use a basic, and presumed user-friendly, feature of a web-browser, the mission is lost. The conclusion here is that Boolean logic needs to be kept in the background for the designers and constructors of knowledge organization system, or for use by moderately expert users, and for it not to be exposed to ordinary end users (Hearst 2011).

Search engines typically rank the results they return. There is an order to the links or items returned. It may be unreasonable to expect that Boolean logic be able to rank the returns of a single search item, say ‘French’. But, if there is already a pre-coordinated, or indexed, ranking of both ‘French’ and ‘cooking’ separately, should Boolean logic be able to help with the ranking of the Boolean combination of ‘French and cooking’? This is related to another point. All the sets discussed earlier are perfectly definite as to what is in them and what is not. Boolean logic works well with this: it has two values True/False, 1/0, Yes/No, is-a-member/is-not-a-member. But there is the view that relevance admits of degrees. So that, for example, some items returned by a search for ‘French’ are more relevant to the User’s interest, and some less relevant. This means that the associated sets of locators are not definite in their boundaries, they are ‘fuzzy’. Boolean logic, with its 0s and 1s leads to ‘crisp’ sets. If, indeed, relevance in knowledge organization needs to be fuzzy, if it needs fuzzy sets, Boolean logic is not appropriate. There have been initiatives to extend Boolean logic, for example, to weighted Boolean logic (Stock and Stock 2013b). The idea here is the indexer, or index process, attaches a number or weight to the index terms and locators; for example, a particular page in a book might be indexed French 0.75 and cooking 0.25. Then the searcher attaches numbers to the search input; for example, search for ‘French 0.3 and cooking 0.7’ and mathematics on the index and input produces an ordered set of locators ranked by relevance. This proposal does not seem to have got very far, and it is easy to find potential reasons why. Indexing itself is unreliable (Weinberg 2009). Adding numbers to that unreliability is not going to help. Searchers struggle to use ordinary Boolean search. Burdening them with additional numbers for the search task is not going to be lightening their load. Then the mathematics is akin to Ptolemy adding epicycles. It is done after the case ad hoc and it does not anticipate the requirements by clear theoretical insight.

But there are deeper problems though. In logic itself, Boolean logic is not ‘fine-grained’ enough to show that many valid arguments are indeed valid. This shortcoming led to the development of predicate logic by Frege, Peirce, and others (Frege 1879; Peirce 1931). Also, there was the proposal of lambda calculus, the calculus of anonymous functions, by Alonzo Church (Church 1940). Now, the validity of arguments is not a central concern of knowledge organization. However, to engage with validity there has to be an analysis of the concepts within the propositions and arguments (indeed, Frege’s main book has the title Begriffsschrift, which means ‘concept writing’). And concepts are absolutely central to knowledge organization. Concepts are used to classify. Concepts are the underlying structure to headers in indexing. Concepts are the meanings of search strings in search. So, knowledge organization needs adequate tools for the analysis of concepts. Boolean logic may be among those tools, but, really, it is the rather more powerful tools of lambda calculus and predicate calculus that are needed.

This shortcoming of Boolean logic for the purposes of knowledge organization was well known to some of the pioneers of knowledge organization. Ranganathan, for example, knew that concepts, topics, subjects, or headings like ‘A comparison of tropical forests with temperate forests’ could not be produced by Boolean operations. (He used ‘loose assemblages’ for these (Ranganathan 1937)). Ranganathan devised many connectors for combining subjects including, dissection, lamination, denudation, loose assemblage, and superimposition. This is to go further than Boolean logic.

The conclusions urged here that are that Boolean logic is not strong enough for every potential use in knowledge organization, and that it is not the best for plain untrained end users. However, we should note that it does still remain relevant for researchers. For example, Kraft et al. (2015, 270) write

It has been speculated that Boolean logic is passé, out of vogue. Yet, researchers have employed p-norms in the vector space model or Bayesian inference nets in the probabilistic model to incorporate Boolean logic. In addition, the use of Boolean logic to separate a collection of records into two disjoint classes has been considered, e.g., using the one- clause-at-a time (OCAT) methodology [Spärck Jones 1971]. Even now retrieval systems such as Dialog and web search engines such as Google allow for Boolean connectives.

[top of entry]

Acknowledgements

I thank the referees. They have provided insightful and valuable suggestions.

[top of entry]

References

Adams, Scott. 1972. “The Way of the Innovator: Notes Toward a Prehistory of MEDLARS”. Bulletin of the Medical Library Association 60 (October): 7.

Bednarek, Alexander R. 1970. “Boolean Algebras”. In Encyclopedia of Library and Information Science DOI: 10.1081/E-ELIS 120008970, 3:369–74. Marcel Dekker.

Boole, George. 1847. The Mathematical Analysis of Logic, Being an Essay Towards a Calculus of Deductive Reasoning. Originally published in Cambridge by Macmillan, Barclay, Macmillan. Reprinted in Oxford by Basil Blackwell, 1951.

Boole, George. 1854. An Investigation of The Laws of Thought on Which Are Founded the Mathematical Theories of Logic and Probabilities. Originally published by Macmillan, London. Reprint by Dover, 1958.

Burris, Stanley. 2018. “George Boole”. In The Stanford Encyclopedia of Philosophy (Summer 2018 Edition), Edward N. Zalta (Ed.), https://plato.stanford.edu/archives/sum2018/entries/boole/.

Chan, Lois Mai, and Edward T. O’Neill. 2010. FAST: Faceted Application of Subject Terminology: Principles and Application. Libraries Unlimited.

Church, Alonzo. 1940. “A Formulation of the Simple Theory of Types”. The Journal of Symbolic Logic 5: 56–68.

Coletti, Margaret H., and Howard L. Bleich. 2001. “Medical Subject Headings Used to Search the Biomedical Literature”. Journal of the American Medical Informatics Association 8: 317–23.

Enderton, Herbert B. 2001. Mathematical Introduction to Logic. 2nd ed. Harcourt Academic Press.

Foskett, Anthony C. 1977. Subject Approach to Information. 3rd ed. London: Clive Bingley.

Frege, Gottlob. 1879. Begriffsschrift. Translated in Jean van Heijenoort, ed. From Frege to Gödel. Cambridge, MA: Harvard University Press.

Goyvaerts, Jan. 2020. Regular-Expressions.Info. 2020. https://www.regular-expressions.info/.

Hailperin, Theodore. 1984. “Probability Logic”. Notre Dame Journal of Formal Logic 25, no. 3, July 1984: 198–212.

Hailperin, Theodore. 1986. Boole’s Logic and Probability. Amsterdam: North-Holland.

Hearst, Marti. 2011. “10: User Interfaces and Visualization”. In Modern Information Retrieval, eds. Ricardo Baeza-Yates, Berthier Ribeiro-Neto. New York: Addison-Wesley. http://people.ischool.berkeley.edu/~hearst/irbook/10/chap10.html.

Hjørland, Birger. 2015. “Classical Databases and Knowledge Organization: A Case for Boolean Retrieval and Human Decision-Making During Searches”. Journal of the Association for Information Science and Technology 66: 1559–1575.

Hjørland, Birger. 2018. “Indexing: concepts and theory”. Knowledge Organization 45, no. 7: 609-39. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/indexing.

Howson, Colin, and Peter Urbach. 1993. Scientific Reasoning?: The Bayesian Approach. 2nd ed. Chicago: Open Court.

Kaiser, Julius Otto. 1911. Systematic Indexing. London: Pitman.

Kleene, Stephen C. 1956. “Representation of Events in Nerve Nets and Finite Automata”. In Automata Studies, 34:3–41. Annals of Mathematics Studies. Princeton, NJ: Princeton University Press.

Kraft, Donald, Erin Colvin, Gloria Bordogna and Gabriella Pasi. 2015. “Fuzzy Information Retrieval Systems: A Historical Perspective”. In Fifty Years of Fuzzy Logic and its Applications, eds. Dan E. Tamir, Naphtali D. Rishe and Abraham Kandel. Cham: Springer, 67-96. DOI: 10.1007/978-3-319-19683-1_15.

Library of Congress Subject Headings. 2020. http://id.loc.gov/authorities/subjects.html.

Library of Congress Subject Headings: Pre- vs. Post-Coordination and Related Issues. 2007. https://www.loc.gov/catdir/cpso/pre_vs_post.pdf.

Lowe, M. Sara, Bronwen K. Maxson, Sean M. Stone, Willie Miller, Eric Snajdr, and Kathleen Hanna. 2018. “The Boolean Is Dead, Long Live the Boolean! Natural Language versus Boolean Searching in Introductory Undergraduate Instruction". College & Research Libraries 79: 517-34”. https://doi.org/10.5860/crl.79.4.517.

McIlwaine, Ia. C. 1997. “The Universal Decimal Classification: Some Factors Concerning Its Origins, Development, and Influence”. Journal of the American Society for Information Science 48: 331–39.

MeSH. 2010. “Medical Subject Headings - Home Page”. 2010. https://www.nlm.nih.gov/mesh/meshhome.html.

OCLC. 2011. “Faceted Application of Subject Terminology (FAST)”. 2011. https://www.oclc.org/research/themes/data-science/fast.html.

Peirce, Charles Sanders. 1931. Collected Papers of C. S. Peirce. 8 vols. Ed. Cambridge, MA: Harvard University Press.

PubMed. 2020. https://www.ncbi.nlm.nih.gov/pubmed.

Ranganathan, Shiyali R. 1937. Prolegomena to Library Classification. 3rd ed. 1967; 1st ed. 1937. Madras: The Madras Library Association.

Ranganathan, Shiyali R. 1952. Colon Classification. 4th ed. Bombay: Asia Publishing House.

Rogers, Frank B. 1953. “Applications and Limitations of Subject Headings: The Pure and Applied Sciences”. In The Subject Analysis of Library Materials, edited by Maurice F. Tauber, 73–82. New York: Columbia University.

Rogers, Frank B. 1960a. “Medical Subject Headings. Preface and Introduction”. In Medical Subject Headings, 1st ed., i–xix. Washington D.C.: National Library of Medicine U.S. Department of Health, Education, and Welfare.

Rogers, Frank B. 1960b. “Review of Taube, Mortimer. Studies in Coordinate Indexing”. Bulletin of the Medical Library Association 42: 380–84.

Shannon, Claude E. 1938. “A Symbolic Analysis of Relay and Switching Circuits”. Transactions of the American Institute of Electrical Engineers 57: 713–23. https://doi.org/10.1109/T-AIEE.1938.5057767.

Spärck Jones, Karen A. 1971. Automatic Keyword Classification for Information Retrieval. London: Butterworths.

Stock, Wolfgang G., and Mechtild Stock. 2013a. “Boolean Retrieval”. In Handbook of Information Science, 241–52. Berlin: Walter de Gruyter.

Stock, Wolfgang G., and Mechtild Stock. 2013b. “Weighted Boolean Retrieval”. In Handbook of Information Science, 266–73. Berlin: Walter de Gruyter.

Stone, Marshall H. 1936. “The Theory of Representations of Boolean Algebras”. Transactions of the American Mathematical Society 40: 37–111.

Taube, Mortimer. 1951. “Functional Approach to Bibliographic Organization: A Critique and a Proposal”. In Bibliographic Organization: Fifteenth Annual Conference of the Graduate Library School, 24-29 July 1950, edited by Jesse H. Shera and Margaret Egan, 57–71. Chicago: University of Chicago Press.

Taube, Mortimer. 1953. Studies in Coordinate Indexing. Washington, D.C.: Documentation Incorporated.

Taube, Mortimer, and Alberto F. Thompson. 1951. “The Coordinate Indexing of Scientific Fields”. Unpublished Paper Read before the Symposium on Mechanical Aids to Chemical Documentation of the Division of Chemical Literature of the American Chemical Society, Sept 4, 1951.

Thompson, Ken. 1968. “Programming Techniques: Regular Expression Search Algorithm”. Communications of the ACM 11: 419–422. https://doi.org/10.1145/363347.363387.

Vickery, Brian C. 1953. “Systematic Subject Indexing”. Journal of Documentation 9: 48–57.

Vickery, Brian C. 1975. Classification and Indexing in Science. 3rd ed. London: Butterworths.

Weinberg, Bella Hass. 2009. “Indexing: History and Theory”. Encyclopedia of Library and Information Sciences, Third Edition, 2277–90.

Wellisch, Hans H. 1991. Indexing from A to Z. H. W. Wilson Co.

Whitehead, C. 1989. “Faceted Classification in the Art and Architecture Thesaurus”. Art Documentation 8: 175–77.

Wolfram, Stephen. 2018. “Logic, Explainability and the Future of Understanding — Stephen Wolfram Writings”. 2018. https://writings.stephenwolfram.com/2018/11/....

WorldCat.Org: The World’s Largest Library Catalog. 2020. https://www.worldcat.org/.

Zafran, Enid. 2010. “Indexing Advice (‘From A to Zafran’)”. http://www.indexingpartners.com/about/indexing-advice-from-a-to-zafran.html.

[top of entry]

Visited times.

Version 1.0, published 2020-02-25
Version 1.1 published 2022-09-06-: quote by Kraft et al. 2015 added.

Article category: Methods, approaches & philosophies

This article (version 1.0) is also published in Knowledge Organization. How to cite it:
Frické, Martin. 2021. “Boolean logic”. Knowledge Organization 48, no. 2: 177-191. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/boolean

©2020 ISKO. All rights reserved.