I S K O

Encyclopedia of Knowledge Organization

Logical division

by Martin Frické

Table of contents:
1. Introduction: kinds of division
2. The basics of logical division
3. History
4. Formalization
5. The rules
6. The status of the rules
7. The process of logical division
8. Conclusion
References
Colophon

1. Introduction: kinds of division

Division used to be a central topic in logic. The logic in question was an Aristotelian style of logic, which was taught and studied prior to the modern logic of Frege, Russell, and others i.e. prior to about 1920. For example, J. J. Toohey (1918) An elementary handbook of logic has a chapter on "Division". See also Jevons (1883, Section II), and Parry and Hacker (1991, Chapter 6). Toohey (1918, Chapter XVI) distinguishes:

Logical division, which is the resolution of a class into the subclasses that compose it (e.g. triangles into obtuse-angled, right-angled, and acute-angled)
Physical division, which is the resolution of an individual thing into the physical parts which compose it (e.g. a particular sword into its hilt and its blade)
Metaphysical division (or mental distinction), which is the resolution of 'objects' into the attributes which they possess (e.g. man into rational, sentient, organic, corporeal, warm-blooded, mortal etc.)
Verbal division, which is the resolution of a word which is a homograph into the synonyms which compose it (e.g. 'palm' into 'palm (kind of tree)' and into 'palm (part of hand)')

Many other similar kinds of division might be imagined (e.g. mathematical division, which might include a partitive factoring of a natural number into its component primes).

Division is obviously important to knowledge organization. Typically, an organizational infrastructure might acknowledge three types of connecting relationships: class hierarchies, where some classes are subclasses of others, partitive hierarchies, where some items are parts of others, and instantiation, where some items are members of some classes (see Z39.19 ANSI/NISO 2005 as an example). The first two of these involve division (the third, instantiation, does not involve division — see below). Logical division would usually be a part of hierarchical classification systems, which, in turn, are central to shelving in libraries, to subject classification schemes, to controlled vocabularies, and to → thesauri. Partitive hierarchies, and partitive division, are often essential to controlled vocabularies, thesauri, and subject tagging systems. Partitive hierarchies also relate to the bearers of information; for example, a journal would typically have its component articles as parts and, in turn, they might have sections as their parts, and, of course, components might be arrived at by partitive division (see Tillett 2009 as an illustration). Finally, verbal division, disambiguating homographs, is basic to controlled vocabularies.

Thus division is a broad and relevant topic. This article, though, is going to focus on logical division.

[top of entry]

2. The basics of logical division

Logical division concerns collections, and sub-collections of those collections. It concerns the family of concepts exemplified by sets, classes, kinds, types, sorts, and similar concepts, and it concerns the subclass-superclass relationships (or subtype-type relationships, or subset-set relationships etc.). There have been many different specific theories of sets, classes, kinds, types, and the like. What is needed to discuss logical division in general is a certain accommodation and gentleness with respect to these different concepts. In this article, the word class will be used to cover any of class, kind, type, sort, set etc. Then, subclass-superclass will be the primary relation of interest.

Logical division divides a class into some of its subclasses, then some of those subclasses into some of their subclasses, and so on, a finite number of times. In general, any class will have many subclasses, but logical division is typically interested only in collections or families of subclasses that "divide up" the original class i.e. the subclasses resulting from a step of division need to be disjoint and not have members in common. A single step of logical division produces something akin to a partition of the original class, then the next steps produce partitions of those partitions, and this process continues in a like manner. An important distinction within the theory of classes is that between intension and extension, what Frege calls Sinn (sense) and Bedeutung (reference) (Tichý 1988). To conceive of, or to define, a class intensionally is to give a property, or concept, which characterizes it. To conceive of, or to define, a class extensionally is to give a listing of its members. Suppose, to give an example, that every red object in the world was also round, and every round object was also red; then the classes red and round would be co-extensive, they would have the same members; in which case, conceiving of classes extensionally, just as listings of their members, the classes red and round would be the same class; there would just be the one class. In contrast, conceiving of the classes intensionally, the classes are different and there are two of them, the property red is a color and the property round is a shape and even if, in our world, everything that was red was round and vice versa, there would be, or could be, other worlds, other possibilities that we can conceive of, in which there are some red objects which are not round, or round objects that are not red.

Logical division has sometimes been treated extensionally, in terms of dividing up listings of members, and sometimes treated intensionally, in terms of dividing up classes produced by properties or characteristics (see Marradi 1990; Howton 2010 for further discussion). A consideration here is whether division is going to be used on classes in mathematics, logic, and other a priori and necessary areas, or on classes in science and everyday matters of fact. Mathematics is extensional; for example, what prime numbers there are, there simply are — there is not some kind of alternative reality in which there are a few more or a few less prime numbers. In contrast, science and everyday matters of fact, are intensional; for example, the class of 19th century mathematical logicians has, as a matter of fact, Frege as one of its members, but it might have been that Frege chose a different line of business, in which case, the same (intensional) class 19th century mathematical logicians would have had a different extension. It is almost always better to treat division using an intensional conception of classes, but in mathematics, logic, and some other areas, an extensional conception can be adequate. With some historical writers, for example Plato, it is not entirely clear whether the division is intensional or extensional (Howton 2010) — to be fair, Plato was writing 2000 years before Frege.

If intensional division is used, the technique would usually be that of adding properties or conditions to the higher level properties; for example, the class animals can be divided into the subclasses animals and warm-blooded and animals and not-warm-blooded, and this is just adding or conjoining the properties of being "warm-blooded" or "not-warm-blooded" to the base property of being an animal.

The division of a class into subclasses produces only classes, and division of those subclasses produces only further classes. Within the domain of logical division, there is no interest in, or theory of, instances i.e. members of those classes. So, for example, logical division may address whether the class man and the class horse are subclasses of the class animal, but there is no interest whatsoever in, for example, whether the individual Socrates is an instance of the class man or of the class horse or of any other class. There is a caveat that can be given here. Nowadays we are perfectly sound on the distinction between subclass and instance (or member); for example, the class old man is a subclass of man, and Socrates is an instance of old man (and of man), but Socrates is not a subclass of old man (nor of man). But this distinction only really comes clear in the 19th century with Cantor and set theory. So pre-19th century materials on class and instance may or may not be perspicuous on the distinction.

In a finite class hierarchy produced by division, the structure is that of tree, i.e. a rooted connected acyclic graph (see Diestel 2012 for an explanation of these terms), and so there are nodes or classes or species that do not have children. These are the "leaves" of the tree — they are the infima species. Division stops at the leaves. Somewhat similarly in the other direction, there is a node or class or species that does not have a parent class. This is the "root" of the tree — it is the summum genus. Division starts with the root class. There is the notion of level of a class or node in a tree, and this is identified by the number of links between the root of the tree and the class. Sometimes, for example in Eighteenth century biology, the levels can have particular names of their own, e.g. "kingdom", "phylum", "family" (Linnaeus 1758).

It is possible to view → classification and division as companions or counterparts. If so, division would be "top-down". Indeed, division has been referred to as "downward classification" (Mayr and Bock 2002; Mayr 1982). The starting point would be a very general class which would successively be narrowed until a suitable classification class was reached. The whole division and narrowing process produces a classification system, a tree of classes. In contrast to division, the plain act of classification, i.e. the action or process of putting items in classes or categories, would normally be "bottom-up". The starting point would be one or more items or individuals, which needed classifying, and they would be classified by putting those with commonalities as members of a suitable narrow class and proceeding upward. Care is needed with the viewpoint that division and classification are much the same, apart from being in different directions The process of classification requires identifying suitable classes with the items as members i.e. it requires consideration of membership or instantiation. In contrast, the process of division has no connection whatsoever with membership and instantiation.

[top of entry]

3. History

There are four important philosophical figures, historically, that set the scene for logical division: Plato (circa 450 B.C.E.), Aristotle (circa 400 B.C.E.), Porphyry (circa 270 C.E.), and Boethius (circa 500 C.E.). And there is one prominent scientist that should be mentioned: Linnaeus (circa 1740 C.E.).

Plato in the Sophist seeks a definition of the form or class or kind sophist, and there is a specific dialectical method that he advocates (Gill 2016; 2010; Howton 2010). It is that of starting with a very general kind, then using division to divide that kind in two, then repeating this process over and over until the exact kind sophist was met. It was as though one were travelling on a journey down a road, and every time the road had a fork, one path was chosen, until the destination was reached. The meeting of a fork, and the choosing of one of the (usually) two possibilities is the technique of division. At the destination point, the process was reversed, or the route retraced, and all the division properties were accumulated together as the definition of sophist. Plato used the same technique in the Statesman to define the kind statesman, and the approach was assumed to be general (Gill 2016; 2010; Howton 2010).

The notion of definition in use here is not that of explaining the meaning of a word (say the word sophist) rather it is that of capturing what it is to be an X (in this case, to be a sophist). It is to grasp what is essential.

Aristotle also offered a theory of definition, in Topics (Smith 1997). This rests on Aristotle's theory of classification (Berg 1982; Smith 2016). In this, it is a species that is defined, and a species is defined by means of a genus and a difference. So, for example, a classification fragment from the history of biology might be

This diagram is illustrating a partial classification hierarchy among classes; so, for example, animal is a subclass of living organism and a superclass of man and horse. An alternative way of describing this is to say that animal is a child class of living organism and a parent class of both man and horse.

All of the members of a classification hierarchy which are children are species — so horse is a species. Any member of the hierarchy which is a parent class is a genus — so, animal is a genus. Then the child species of a specific genus are separated one from another, i.e. from their sibling species, by means of the differences. For example, Aristotle thought that what was characteristic of man was that man had the capability of reasoning i.e. was rational. (The other species' differences are not illustrated in the diagram.)

It is the species that are defined, and they are defined by identifying their parent i.e. their genus and putting that together with the differentiae which is the difference which separates or distinguishes them from their siblings. So, an example definition is

man =_df. animal having the capacity to reason

All such definitions have the form

<species> =_df. <genus> <difference>

When a class or species is defined this way, the defining properties on the right hand side of the definition are essential properties that all instances of the species must have. Definition, Aristotelian definition, is the definition of a species by means of its genus and difference (Berg 1982; Smith 2004). (Just as a historical note, Aristotle did not use classification diagrams, that came later inspired by Porphyry, and also Aristotle did not use the word species, that also came later, with Porphyry and Boethius.)

Like Plato, Aristotle sometimes used the method of division to produce essential definitions. However, he was critical of Plato's approach to division. His view was that Plato-style division could be used as a heuristic to discover essential definitions, but the method was not strong enough as a method of proof to prove that the tentative essential definitions were indeed truly correct and that they captured the relevant essences. Aristotle argues this in Posterior Analytics II 3-10, and Prior Analytics I 31 (Smith 1989; 2016) and Howton (2010) provides a discussion.

Porphyry was a commentator on Aristotle, in particular Porphyry's Isagoge et in Aristotelis Categorias commentarium is an introduction to logic and a commentary on Aristotle's Categories. Isagoge became the standard text for logic in the Middle Ages; indeed, it served as a basic introductory text in philosophy for 1000 years (Eyjólfur 2015). In it, Porphyry introduced the "Tree of Porphyry" and these are classification trees, produced by division, where the division is a bifurcation (or dichotomy or exhaustive division) at each step (Verboon 2014; Hacking 2007). Jevons (1883, 232) provides the example

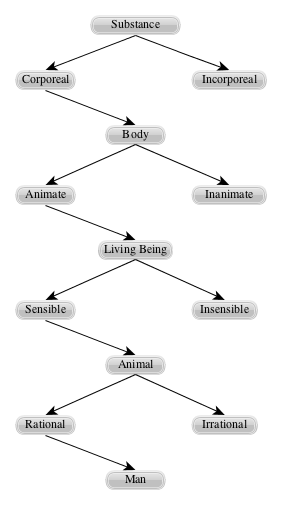
Jevons has presented the tree in a certain way, tidying up much older diagrams. He has omitted Latin annotations. He has omitted potential children of the negation classes e.g. incorporeal does not have any children that are shown in the diagram. Then what seem to be the immediate children of a genus are in fact sometimes the differentiae which are then collected back into the real genus immediate child, for example, animal descends left to rational, which is the difference, and animal and rational are collected together to form man which is the child of animal.

Boethius was also an influential commentator on Aristotle's work (Arlig 2015). He was the main medieval authority on division, and he wrote a handbook on division (Magee 1998). Boethius also provided a commentary on Porphyry's Isagoge and translated it. It is in the manuscripts of those translations that the first diagrams of the Tree of Porphyry appear (Verboon 2014). So Boethius is important in conveying these ideas to a wider audience.

In the history of science, Linnaeus was probably the most prominent scientific classifier of the natural world. He used "binomial nomenclature", which is the identifying of classes by means of genus and species (Linnaeus 1758). At least some of the time, Linnaean classification structures were produced by logical division, especially logical division using dichotomy or bifurcation e.g. into warm-blooded and not-warm-blooded, into feathered and not-feathered, etc.

[top of entry]

4. Formalization

It will be useful to employ some formalization or symbolization. Naïve set theory is suitable. There is a caution that should be given connected with the use of naïve set theory in this context. Set theory is extensional; that is to say: sets are defined by their members; so if a set "changes" its members it becomes a different set. But that is not really what is required for discussing Aristotelian classification and division. Instead, what is required is an intensional notion where a class is identified by its defining conditions or defining function so that the class can change its extension without becoming something else. Aristotle's kind man is a single kind, not multiple kinds as men are born or die. The naïve set theory required here should be understood intensionally.

In naïve set theory, there is the abstraction or comprehension or "set-builder" notation

{x:Φ(x)}

In this abstraction, the x is a binding variable and the Φ(x) is a "open sentence" which is a sentence with zero or more free occurrences of the variable x. The abstraction notation is read "the x such that Φ(x)". For example, in a suitable predicate logic

Sophist(x)

is an open sentence with one free occurrence of x, it would be read "x is a sophist", and

{x:Sophist(x)}

is a well-formed abstraction which identifies the class of sophists. It would be read as "the class of sophists".

This notation, or notational variants of it, are commonplace in many computer programming languages including Python and Mathematica; it is used to denote lists or sets or classes, which are defined by one or more conditions.

In all formalizations suitable for discussing classes, the following result will be available, writing it first in natural language,

if one class is a subclass of another, then all items possessing the defining condition for the first will possess the defining condition for the second

for example, if the class sophist is a subclass of the class man, then anything that is a sophist is also a man. Putting this slightly more formally, using < to mean "subclass":

If {x:Φ(x)} < {x: Ψ(x)} then ∀x (Φ(x) → Ψ(x))

Then, creating a child by division is merely the conjoining of a predicate or condition to the parent condition, for example, making the step from

{x: Ψ(x)}        /*parent*/

to

{x:(Ψ(x)& Φ(x))}     /*child*/

[top of entry]

5. The rules

Toohey (1918, Chapter XVI) offers the four standard rules for logical division:

RULE I: The dividing members must be mutually exclusive as regards the basis employed in the division.

This is desirable so that no species is included in another. This would be violated, for example, if magazines were divided into scientific, literary, and mathematical (because scientific includes mathematical). The rule asserts that in a class hierarchy, sibling classes i.e. child classes of the same parent must not have any members in common. That is:

~∃x(MemberOfChild₁(x) & MemberOfChild₂)(x))

[for each of the pairs of child classes of the particular parent classes; the predicate MemberOfChild_i(x) means "x is a member of the i-th child" ]

This condition is exclusivity. It is sometimes called "pairwise disjoint" (because the sibling classes are pairwise disjoint).

RULE II: The dividing members must together be co-extensive with the class or genus which is divided.

This is a condition of exhaustivity: everything in a parent class must be in at least one of its child classes. The reason that this is desirable is that all the species (of each specific genus) need to be listed. This might go awry in one of two ways. There could be too many (exclusive) children. This would mean that some of the child classes would always be empty: they would never have instantiating members. They would be superfluous, and never have a role to play. So, simplicity or parsimony would suggest removal of these non-working empty classes. (This is a very Aristotelian move: for Aristotle, all classes had to have instances — there were to be no empty classes (Berg 1982).) The other way that exhaustivity might be violated is if there were two few child classes so that there were some members of a parent that were not members of any of its children. This is undesirable because it is an aim to identify all the species and this violation would just mean that the aim had not been carried out. The requirement is

∀x(MemberOfParent(x)→(MemberOfChild₁(x) v MemberOfChild₂(x) ...))

[for each of the parents and their children; the predicate MemberOfParent(x) means "x is a member of a parent"; the predicate MemberOfChild_i(x) means "x is a member of the i-th child"]

This condition is sometimes called "coverage" or "cover". The children need to have the same coverage as their parent.

RULE III: Each process of division must have only one basis.

Toohey (1918, 160) justifies this:

If this rule is violated, the result may be that some objects are included in more than one species. If men were divided into Americans, Englishmen, Irishmen, Frenchmen, Germans, mechanics, and artists, two bases would be employed, namely, nationality and vocation, and some men would be included in more than one species; for example, artists who are French men, and mechanics who are Germans.

In a way, this is to protect Rule 1 (exclusivity). If one base is used, say Americans, Englishmen, Irishmen, Frenchmen, Germans, it can be known in advance that exclusivity is satisfied because the classes are pairwise disjoint (i.e. no American is an Englishman etc.). But if a second basis is introduced, for example: vocation, there is a muddiness. It could be, as it happens, that no present artist is a mechanic and no present artist or present mechanic is any of American, English, etc., but this would be a somewhat fragile arrangement that awaits, for example, the arrival of a French artist whose appearance would break the exclusivity. In the modern day, Buchanan (1979) gives an example from the London Education Classification. In this, the class of educands, who are the people being educated, is divided into the classes teenager, adult, older person, parent and housewife. Teenager, adult, older person is a division produced on the basis of age. The class parent arises on the basis of a family relationship, and the class housewife on the basis of occupation. The division is not made using one basis. It may have been, as a matter of fact, and for a short or long period of time, that the subclasses were exclusive and exhaustive. But the shortcoming with it is obvious: it is quite possible for a housewife to be a parent (or an adult a parent, etc.). So it is prudent to use one basis. What is one basis? It is any simple basis that guarantees exclusivity.

Rule III has a historical connection with Aristotelian essentialism. The theme is that an essential characteristic needs to be a single characteristic. So when a genus is divided into species, the differentiae need to be single properties not complex compounds of properties. That, in itself does not require that the single characteristics be of the same kind, but remember sibling species are species of the same genus, it would be strange if the essential properties were radically different one from another.

RULE IV: In a series of divisions and subdivisions each genus or class should be divided into its proximate members or species.

This relates to the number of levels in a classification tree, or the richness of a tree. A parent class may have children, and the children may have children (which are descendants of the parent), and so on, down to some leaves, which themselves do not have children. It may be possible, depending on the choice of basis or bases, to go from the parent to the leaves in one step or, alternatively, in many steps. Rule IV requires that the number of steps be maximal, that each individual basis makes the smallest step i.e. that to the proximate species. The reason for this is that Aristotelian division is really a process of creating a definition by teasing out all the information or richness that is in the initial parent class, and small divisions to the proximate species is the way to do this. Divisio non faciat saltum (division should not make a leap).

[top of entry]

6. The status of the rules

In the modern day, a classification satisfying Rules I and II are often described as meeting the "JEPD" condition (Jointly Exclusive Pairwise Distinct condition). Rule III has a somewhat indefinite status. Prior to about 1800, Aristotelian classification was aiming to yield a classification of biological species. But it failed in that domain. One reason was that members of a biological species often possessed some, but not all, of a manifold of characteristics — there was no single property possessed by all members of a single species. And this motivated a move to classification on the basis of → cladistics, that is, on the bases of common ancestry rather than common characteristics. (Of course, species with common ancestry did tend to share at least some common characteristics but that is, so-to-speak, a smoke screen rather than the driving principle.)

Relevant at this point is the distinction between natural kinds and artificial, or created or constructed, kinds. The former are part of the furniture of the world, the latter are an artificial creation devised for a particular purpose. Lions and tigers are natural kinds, whereas Toohey's scientific, literary, and mathematical magazines are artificial kinds. It is our scientific theories, the successful ones, that tell us what is or is not a natural kind. Aristotelian essentialist classification and division failed with animate natural kinds. With living organisms, there are no suitable differentiae, bases and essential properties. As Mayr and Bock (2002, 172) write

no adequate classification of kinds of organisms can be achieved that does not reflect the evolutionary theory of common descent.

Aristotelian classification has been partially successful with inanimate natural kinds (for example, with the classification of chemical elements). But where it can be used successfully is with artificial kinds. A classifier doing division can design a system so that, for example, Rule III is satisfied. Artificial kinds also provide an independent motivation for Rule IV. Classification-by-division classifications make assertions and contain compact knowledge. For example, assume for one moment that magazines have been classified as a subclass of periodicals, in which case the classification itself makes the assertion that "All magazines are periodicals", and this is a true or false assertion and is or is not knowledge as the case may be. Suppose it is knowledge, it is a compression in the following way. Consider a few magazines, e.g. Vogue, Sports Illustrated etc. These are magazines, they are also periodicals. But the latter knowledge does not have to be noted in its own right for each individual instance of a magazine, it can be extracted by inference from the classification schema (e.g. if Vogue is a magazine, and all magazines are periodicals, ipso facto, Vogue is a periodical). This means that classifications that have many levels are rich and contain much knowledge. As Rule IV advises: have many levels!

[top of entry]

7. The process of logical division

The process of logical division proceeds as follows. There is a starting class, say

{x:A(x)}

and this is divided into exclusive and exhaustive immediate subclasses, say

{x:B(x)}
{x:C(x)}
{x:D(x)}
etc.

How many immediate, sibling, subclasses there should be is a bit of a question. Some historical figures, e.g. Porphyry, divided a class in two, so, for them, logical division is a process of bifurcation or dichotomy. Let us pursue that for one moment. So, schematically, the division is of

{x:A(x)}

into

{x:B(x)}
{x:C(x)}

That B and C are subclasses of A means that anything that is a B is also an A, and anything that is a C is also an A i.e.

∀x(B(x)→A(x))
∀x(C(x)→A(x))

That the subclasses B and C are exclusive means that anything that is a B is not a C and anything that is a C is not a B i.e.

∀x(B(x) ≡ ~C(x))

That the subclasses B and C are exhaustive of the items in A means that anything that is an A is either a B or a C i.e.

∀x(A(x)→(B(x) ∨ C(x)))

The Rule III requirement that there be a uniform basis for the division is hard to capture. It really needs to guarantee that subclasses (in this case, B and C) are exclusive. One way of achieving this, in the case of bifurcation, is to define one of the subclass conditions as being the negation of the other i.e. to define C as being ~B and then, for clarity, to cease using C altogether). The result is that of dividing

{x:A(x)}

into

{x:B(x)}
{x:~B(x)}

Then this single bifurcation step is repeated with the children, and the children's children as many times as it desired. Defining one subclass as being the "negation" or complement of the other, has the nice property that it also satisfies exhaustivity (i.e. Rule II).

While repetitive bifurcation has some attractive properties, it also has some extremely undesirable features. It leads to a tall narrow tree in which almost everything is a descendant of many negation classes and this plays havoc with ideas of genus and species. What one would expect if there were genuine notions like genus and species is that (a) there would be, or could be, more than one species of the same genus i.e. that there could be several species of the same level, and (b) that being a genus would amount to the possession of some positive property, not a negative one. But this does not happen in a bifurcated tree. For example, suppose there are three classes of interest: animal, man, and horse and bifurcated division is used on animal to produce the man and not-man subclasses; in which case man would be a species of the genus animal and it is of level 1; but what is to happen with horse? It cannot be produced by immediate bifurcated division from animal because animal already has two subclasses (i.e. man and not-man). Likely it will be produced by a bifurcated division of not-man, in which case the species horse would have the genus not-man and be of level 2 (whereas what is desired is that horse has the same genus as man and be of level 1). Jevons (1883, 237) writes

it would be very awkward if we divided the counties of England into Middlesex and not-Middlesex; the latter into Surrey and not-Surrey; the latter, again, into Kent and not-Kent. Dichotomy is useless, and even seems absurd in these cases

In sum, bifurcation is of limited use.

Generalization from bifurcation to that of having arbitrarily many children is fairly immediate, but problems can arise. The main problems concern satisfying exclusivity and exhaustivity, and knowing that those conditions are met. In areas like logic or mathematics, it often can be known that conditions are exclusive and/or exhaustive (for example, the division of rectilinear figures into 3-sided, 4-sided, and 5-sided is an exclusive division). However, in science or in the observable empirical world, it is hard to have such certainty (for example, dividing the class of vertebrate animals into mammalia, birds, reptiles, and fish may or may not be exclusive and may or may not be exhaustive).

There is a move that is sometimes made with empirical division that helps with the exhaustive condition, and that is to have a catch-all "everything else" class. Suppose the preliminary thought is to divide vertebrate animals into the four subclasses mammalia, birds, reptiles, and fish, and a worry is whether these are exhaustive. A remedy is to have a fifth subclass and to divide vertebrate animals into the five subclasses mammalia, birds, reptiles, fish, and everything else. A catch-all subclass might always be used with division. Of course, a catch-the-rest class might often be empty (if the original candidate division was genuinely exhaustive in itself), and empty classes (or subclasses) would not be appealing to pure Aristotelians.

Mills (2004, 554) speaks of this in connection with information resources and information retrieval:

The constituent species collectively must be coextensive with the extension of the genus. The obvious difficulty encountered here is that of our imperfect knowledge. This can be overcome in a technical sense by the process of dichotomy, in which one species is named and all the others are covered by its negative, e.g., the array (Buildings by material) could give just two classes, brick buildings and nonbrick buildings, and this would exhaust the array — no buildings would be missed. In practice, of course, all significant kinds of other materials would be enumerated with a possible residual class for "Others."

With a classification produced properly by logical division, the leaves satisfy the J.E.P.D. condition and so too do all the levels above the leaves. It is the leaves that do the actual classifying. That is, an object to be classified is identified by being recognized as being a member of a particular leaf (then the object is a member of all the superclasses of that leaf tracing a branch right up to the root). Leaves, as opposed to non-leaf nodes, are used for the classification because that provides maximum information and specificity about the classified items. As mentioned, the leaves are exclusive and exhaustive, so all items in the relevant domain have a place in the classification.

It should perhaps be noted that many library classifications do not satisfy the J.E.P.D. condition, and thus they should not be regarded as pure Aristotelian classifications that either were, or might have been, produced by logical division. For example, in the Dewey Decimal Classification (DDC), a work like John Keats's The Works of John Keats (complete Poetry and selected Prose) is classified as English & Old English Literatures 820. This class, 820, is an internal class with children, but the Keats's work is not a member of any of the children of 820 i.e. the subclassing at this point is not exhaustive (see Frické 2012, Section 5.4 for a discussion).

[top of entry]

8. Conclusion

Logical division produces classifications with admirable qualities. Everything has a place in a leaf, its own unique place, and the classification schedule embodies the maximum amount of general information about the items being classified. Logical division can work well in the realm of logic, mathematics, and other non-empirical and a priori areas. But the realm of the empirical is more challenging. Attempts to use division on animate natural kinds were abandoned, around the mid-19th century. Division can be used on non-animate natural kinds e.g. in chemistry. But by far its best potential lies with completely artificial classifications which have been devised, or conjured up, to meet a particular purpose e.g. taxpayers' incomes, document kinds, retail shops' inventory, file types, factories manufacturing capabilities, → metadata values, etc.

Logical division can also have a role in → faceted classification, which is a favored form of classification in the modern day (Broughton 2006; Classification Research Group 1955; Frické 2011; Hjørland 2012). To take a simple example. Say a jeweler sells rings. The jeweler might first create a classification tree by division on the class of rings using purchase price as a driving principle — dividing into expensive, economy, and modestly priced, then dividing those classes into particular price bands. The jeweler might then create a second classification tree by division on the same class of rings using gemstone as a driving principle — dividing into precious and semi-precious, then dividing those classes into diamonds, sapphires, etc. Then both these classification trees will be used simultaneously to create a faceted classification of the rings for sale (into expensive diamond rings, modestly priced diamond rings, economy sapphire rings, etc.). The overall classification structure is that of two trees with two roots, and any particular ring is classified by being placed in two leaves, one from each tree. The entire structure has not been produced by a single run of processing a class by division. However, logical division has played its part.

Logical division is a strong element in the Aristotelean tradition which is still influential in many fields, including in the → facet-analytic tradition in knowledge organization mentioned above (see Mills 2004 as an example). The Aristotelean tradition itself has been challenged by influences from, in particular, empirical and → genealogical approaches (Hjørland 2002; Kwasnik 1999; Hjørland 2013). Separately, the idea that a single shared property can define a useful real world class, or, to phrase it differently, that "groupings by singular similarity" can produce a useful classification class, has been criticized by Rosch's prototype theory and by Wittgenstein's concept of family resemblances (Jacob 2004; Rosch 1973; 1975; 1978; Rosch and Mervis 1975; Rosch et al. 1976; Wittgenstein 1963). In turn, not everyone is convinced by Rosch's and Wittgenstein's reasoning in this setting. There are those who argue that grouping by singular similarity is perfectly sound (see, for example, Sutcliffe 1993; 1994; Frické 2013).

[top of entry]

References

ANSI/NISO, National Information Standards Organization. 2005. ANSI/NISO Z39.19-2005: Guidelines for the Construction, Format, and Management of Monolingual Controlled Vocabularies. Bethesda, Maryland, U.S.A: NISO Press.

Arlig, Andrew. 2015. "Medieval Mereology." http://plato.stanford.edu/archives/fall2015/entries/mereology-medieval/.

Berg, Jan. 1982. "Aristotle's Theory of Definition." Atti del Convegno Internazionale di Storia della Logica, San Gimignano, 4–8 December 1982, Bologna: CLUEB, 1983:19-30.

Broughton, Vanda. 2006. "The need for a faceted classification as the basis of all methods of information retrieval." Aslib Proceedings: New Information Perspectives 58 (1/2):49-72.

Buchanan, Brian. 1979. Theory of Library Classification. London: Clive Bingley.

Classification Research Group. 1955. "The need for a faceted classification as the basis of all methods for information retrieval." Library Association Record 57 (7):262-8.

Diestel, Reinhard. 2012. "Graph Theory." In http://diestel-graph-theory.com/2016, vol. 43, Issue 6, pp. 475-484..

Eyjólfur, Emilsson. 2015. "Porphyry." Accessed 7/20/2016. http://plato.stanford.edu/archives/sum2015/entries/porphyry/.

Frické, Martin. 2011. "Faceted classification: Orthogonal facets and graphs of foci?" Knowledge Organization 38 (6):491-502.

Frické, Martin. 2012. Logic and the Organization of Information. New York: Springer.

Frické, Martin. 2013. "Reflections on Classification: Thomas Reid and Bibliographic Description." Journal of Documentation 69 (4):507-522.

Gill, Mary Louise. 2010. "Division and Definition in Plato's Sophist and Statesman." In Definition in Greek Philosophy, edited by David Charles, 172-201. Oxford: Oxford University Press.

Gill, Mary Louise. 2016. "Method and Metaphysics in Plato's Sophist and Statesman." Accessed 7/26/2016. http://plato.stanford.edu/archives/spr2016/entries/plato-sophstate/.

Hacking, Ian. 2007. "Trees of logic, trees of Porphyry." In Advancements of Learning: Essays in Honour of Paolo Rossi, edited by J.L. Heilbron. Firenze: Leo S. Olschki.

Hjørland, Birger. 2002. "The method of constructing classification schemes: a discussion of the state-of-the-art." Proceedings of the the 7th International ISKO Conference, Granada, Spain, July 10-13.

Hjørland, Birger. 2012. "Facet analysis: The logical approach to knowledge organization." Information Processing and Management. doi: http://dx.doi.org/10.1016/j.ipm.2012.10.001.

Hjørland, Birger. 2013. "Theories of knowledge organization — theories of knowledge." 13th Meeting of the German ISKO (International Society for Knowledge Organization), Potsdam.

Howton, Robert Fuselier. 2010. "The Method of Division and Aristotle's Criticism of Platonic Philosophy." Philosophy, Texas A&M University.

Jacob, Elin K. 2004. "Classification and categorization: a difference that makes a difference." Library Trends 52 (3):515-40.

Jevons, W. Stanley. 1883. The Elements of Logic. London: Sheldon & Co.

Kwasnik, Barbara H. 1999. "The Role of Classification in Knowledge Representation and Discovery." Library Trends 48 (1):22-47.

Linnaeus, Carl. 1758. Systema naturæ per regna tria naturæ, secundum classes, ordines, genera, species, cum characteribus, differentiis, synonymis, locis. 1 (10th ed.). Stockholm: Salvius.

Magee, John. 1998. Anicii Manlii Severini Boethii De divisione liber: Critical Edition, Translation, Prolegomena, and Commentary. Vol. 77. Leiden: E. J. Brill.

Marradi, Alberto. 1990. "Classification, Typology, Taxonomy." Quality and Quantity XXIV (2):129-157.

Mayr, Ernst. 1982. The Growth of Biological Thought. Cambridge, MA: Harvard University Press.

Mayr, Ernst, and W. J. Bock. 2002. "Classifications and other ordering systems." J. Zool. Syst. Evol. Research 40:169–194.

Mills, Jack. 2004. "Faceted classification and logical division in information retrieval." Library Trends 52 (3):541-570.

Parry, William T., and Edward A. Hacker. 1991. Aristotelian Logic. New York: State University of New York Press.

Rosch, Eleanor. 1973. "Natural categories." Cognitive Psychology 4 (3):328-350.

Rosch, Eleanor. 1975. "Cognitive representations of semantic categories." Journal of Experimental Psychology: General 104:192-233.

Rosch, Eleanor. 1978. "Principles of Categorization." In Cognition and Categorization, edited by Eleanor Rosch and B. Lloyd, 27-48. Hillsdale, N.J.: Lawrence Erlbaum.

Rosch, Eleanor, and C. B. Mervis. 1975. "Family resemblances: Studies in the internal structure of categories." Cognitive Psychology 7 (4):573-605.

Rosch, Eleanor, C. B. Mervis, W. Gray, D. Johnson, and P. Boyes-Braem. 1976. "Basic objects in natural categories." Cognitive Psychology 8 (4):382-439.

Smith, Barry. 2004. "The Logic of Biological Classification and the Foundations of Biomedical Ontology." In Invited Papers from the 10th International Conference in Logic Methodology and Philosophy of Science, Oviedo, Spain, 2003, edited by Dag Westerståhl. North Holland: Elsevier

Smith, Robin. 1989. Aristotle's Prior Analytics. Indianapolis: Hackett.

Smith, Robin. 1997. Aristotle, Topics I, VIII, and Selections. Oxford: Clarendon Press.

Smith, Robin. 2016. "Aristotle's Logic." Accessed 7/19/2016. http://plato.stanford.edu/archives/spr2016/entries/aristotle-logic/.

Sutcliffe, John Philip. 1993. "Concept, Class, and Category in the Tradition of Aristotle." In Categories and Concepts: Theoretical Views and Inductive Data Analysis, edited by James Hampton, Ryszard S. Michalski, Peter Theuns and Iven Van Van Mechelen, 35-64. London: Academic.

Sutcliffe, John Philip. 1994. "On the logical necessity and priority of a monothetic conception of class, and on the consequent inadequacy of polythetic accounts of category and categorization." In New Approaches in Classification and Data Analysis, edited by Edwin Diday, 55-63.

Tichý, Pavel. 1988. The foundations of Frege's logic. Berlin: Walter de Gruyter.

Tillett, Barbara B. 2009. "Definition of Aggregates as Works: Tillett Proposal." Accessed 10/10/2011. http://www.ifla.org/files/cataloguing/frbrrg/aggregates-as-works.pdf.

Toohey, John J. 1918. An Elementary Handbook of Logic. New York: Schwartz, Kirwin, & Fauss.

Verboon, Annemieke. 2014. "The Medieval Tree of Porphyry: An Organic Structure of Logic". In The Tree. Symbol, Allegory and Structural Device in Medieval Art and Thought, International Medieval Research, 20., edited by A. Worm and P. Salonis, 83-101. Turnhout: Brepols.

Wittgenstein, Ludwig. 1963. Philosophical investigations by Ludwig Wittgenstein. Translated by G. E. M. Anscombe. English text reprinted. ed. Oxford: Blackwell.

Visited times since 2019-11-13 (3 years after first publication).

Article category: Methods, approaches & philosophies

This article (version 1.0) is also published in Knowledge Organization. How to cite it: Frické, Martin. 2016. “Logical division”. Knowledge Organization 43, no. 7: 539-49. Also available in ISKO Encyclopedia of Knowledge Organization, eds. Birger Hjørland and Claudio Gnoli, https://www.isko.org/cyclo/logical_division
To quote text edited in a later version, you should save it in the Wayback Machine and cite the saved version.

©2016 ISKO. All rights reserved.