I S K O

Encyclopedia of Knowledge Organization

Ideal language

by Steven Laporte

Table of contents:
1. Introduction
2. Natural and ideal language
    2.1 Ideal or merely universal?
    2.2 Natural and artificial languages and semiotic systems
    2.3 Key components of ideal language
    2.4 Knowledge Organisation Systems (KOS) and ideal language
    2.5 The Tower of Babel and the monogenetic hypothesis
    2.6 A priori philosophical languages
3: Ideal languages in the Middle Ages and early Modern period
    3.1 Ramon Llull and the Ars Magna: 3.1.1 A topical outline of Llullian combinatorics; 3.1.2 The Arbor scientiae; 3.1.3 Llull’s legacy
    3.2 Leibniz and the Lingua Generalis: 3.2.1 Coding language; 3.2.2 Leibniz’s Legacy
4. Ideal language in the modern world
    4.1 The ambitions of logical positivism: 4.1.1 The limits of logic; 4.1.2 The language of the mind; 4.1.3 Language by machines; 4.1.4 Formal concept analysis
5. The linguistic turn
6. Conclusion
Endnotes
References
Colophon

Abstract:
This contribution discusses the notion of an ideal language and its implications for the development of knowledge organization theory. We explore the notion of an ideal language from both a historical and a formal perspective and seek to clarify the key concepts involved. An overview of some of the momentous attempts to produce an ideal language is combined with an elucidation of the consequences the idea had in modern thought. We reveal the possibilities that the idea opened up and go into some detail to explain the theoretical boundaries it ran into.

[top of entry]

1. Introduction

The search for an ideal language [1] is a complex matter that spans millennia and crosses cultural boundaries. Due to the broadness of its scope, any attempt of summarizing this subject runs the risk of leaving out compelling elements. Much depends on the viewpoint that is taken, for without a clear perspective, the search for the ideal language can easily appear to be an obscure and utopian curiosity. Possible angles include the linguistical, semiotic, philosophical, mathematical and historical. Even though this article will contain elements from all these fields, the main perspective is that of → knowledge organization (KO).

Immediately at the outset we can raise a drastic question: Is an ideal language really a language? Just consider the idea of an artificial language that aspires to be a perfect system for ordering knowledge and communicating it. Can such a system, exist and still be compatible with the other functions of language, like direct interaction and the communication of information and emotion?

In Western, as well as in Eastern philosophy, a general feeling of inadequacy is often directed towards natural languages with respect to clarity of meaning [2]. In the West this is most explicitly the case in the rationalist tradition. In the East too, the limits of language have been pointed out, for example in an ancient statement, attributed to Confucius, which states that “Writing does not exhaust words, and words do not exhaust meaning". (Tang 1999, 2). Ideal languages aim to overcome this deficiency and in doing so, they need to address the issue of knowledge organization.

Knowledge organization as an independent discipline is very much about → knowledge organization systems (KOS) and indexing languages, such as classification systems, thesauri and ontologies. Both KOSs and indexing languages can vary in complexity and scope, but share a common set of functions that include the elimination of ambiguity, controlling synonyms, the establishment of hierarchical and associative relations and the clear presentation of properties (Zeng 2008). A number of these properties are also the requirements for creating an ideal language, perhaps even to the extent that we may consider these ideal languages to be knowledge organization systems in themselves. Contrary to natural languages, the principal aims of both KOS and ideal language are not mere communication, but the elimination of ambiguity and the establishment of a one-to-one correspondence between terms and concepts.

Another important issue that characterizes the search for an ideal language is its ambition to produce a context-free structure for representing and organizing knowledge. Again, similar claims have been made about relationships in KOSs, in particular for thesauri as argued by Elaine Svenonius (2004) and discussed in depth by Birger Hjørland (2015).

Even though at a first glance there seems to exist a distinct relationship between ideal- and natural languages, it quickly becomes apparent that the disparities are considerable. It is true that, like natural languages, an ideal language can provide a form of communication. But what they communicate are not plain everyday experiences, instructions and emotions, but rather clear and distinct concepts and elements of knowledge. This illustrates once again that the word language in the expression “ideal language” can be profoundly misleading. Like classification systems, mathematical models or even musical notation devices, an ideal language is a semiotic system. But in addition to being a practical and consistent means of combining symbols with concepts, it proclaims to be the perfect or “ideal” system to achieve this. This claim is ultimately grounded on the basic assumption that a language that is constructed from first principle — instead of being moulded by contextual phenomena — can appropriate the compelling characteristics of a logical argument.

One can safely argue that even the very idea that there can exist a means to communicate knowledge in an ideal way, presupposes a typical epistemological viewpoint. It suggests an underlying set of assumptions that is akin to the theory of “logical atomism” as it was proposed by Bertrand Russell at the start of the 20th century (Russell 1919). In this view there exist only a limited number of logical elements and all complex subjects are a combination of these “atomic” elements. Similarly, when considering an ideal language, we can also recognise this effort to reduce complex matters to their constituent parts.

The special purpose of the present article is to search for evidence that can relate the search for an ideal KOS to the general historic search for an ideal language. This will put the philosophical underpinnings of KOSs in a broader context and a provide a deep historical perspective on the general enterprise of systematic knowledge organization.

The article starts by considering the concepts of natural language and ideal language in relation to similar concepts such as artificial language, universal language, special language and terminology. Throughout the texts we aim to constitute a clear terminology that allows us to properly disentangle the notion of an ideal language from all misconceptions.

[top of entry]

2. Natural and ideal language

2.1 Ideal or merely universal?

Closely related, but not quite identical to the concept of an ideal language, is the notion of a universal language. The most striking way in which the difference becomes apparent is in the basic condition that must be met to consider a language universal: namely that it should be universally understood. Strictly speaking a universal language does not necessitate the language itself to possess any remarkable internal features. The effectiveness of its universal ambitions rests solely in the generality of its use.

An ideal language on the other hand does not imply that it is universally used, even though most historic attempts to construct such languages expressed this ambition. The main distinguishing features of an ideal language lay in its internal structure. The way in which an ideal language is constructed — its grammar or logical configuration — make it unique to the point that anybody who encounters it would be compelled to use it.

Examples of universal languages, or at least of languages that displayed the ambition of functioning as such, are plentiful. The most common example in Western history would arguably be Latin. Spread by the conquering Romans, Latin established itself as the main language for trade, law, knowledge exchange and affairs of state throughout Europe (Richardson 1991). After the decline of the Roman empire it was perpetuated as the established language of religious practices as it was widely endorsed by the Roman Catholic Church. But also, outside the Church’s scope it became the language of choice for European scholars and early scientists to be used in textbooks and scholarly communication.

Several other languages have competed for the status of ‘Lingua Franca’ throughout Western history. Italian, French and most recently English have succeeded each other as the dominant languages — or second languages — of the European continent and far beyond.

The success of these languages owed very little to any special properties. Mostly their success followed in the footsteps of the military or cultural domination of their respective countries of origin. A phenomenon that can be also be observed outside Europe, for example by the spread of Mandarin in China and Spanish and Portuguese in South America. Although the benefits of the use of a common language in international affairs are generally accepted, existing natural languages with universal ambitions are never neutral because they are typically laden with the cultural values of their countries of origin (Van Parijs 2004).

But apart from military conquest, there have been other perspectives that were adopted to advance a language as a universal standard. Most notable is the introduction of Esperanto in the late 19th and early 20th century (Smokotin and Petrova 2015). Esperanto is an artificial language, comprised of notions that were borrowed from several existing (mostly European) natural languages. These were combined in ways that were easy to teach and learn.

Although artificial languages like Esperanto are constructed according to a set of rational guiding principles, they too do not qualify as examples of an ideal language in the strict sense. The reason they formed in the way that they did, was the result of practical considerations. A more recent example is Lojban. Lojban is a language that is constructed to be syntactically unambiguous. The purpose here was not just to make a language that is easy for humans to learn, but also to invent one that could easily be parsed by a computer (Speer and Havasi 2004).

For an artificial language to be able to be considered ideal, however, the internal structure would have to present itself out of logical necessity, rather than pragmatism. This approach takes us into a realm that is dominated by notions like classes, properties, symbols and the logical relations between them. Because of this formal build-up, an ideal language deviates significantly from natural languages. It completely misses the power of expression of the latter, which was often precisely the result of a certain level of indeterminacy caused by a series of historical serendipities. And yet all attempts to form an ideal language were made with the intention of constructing a way of communicating that would be as clear and efficient as possible. Clearly the creators of an ideal language held the capacity of language to communicate clear concepts efficiently in higher esteem than its capacity for power of expression in the poetic sense.

[top of entry]

2.2 Natural and artificial languages and semiotic systems

By natural language we generally mean a language that has formed without following a pre-set plan or according to the will of a single author. The development of natural languages is generally understood to take place gradually over time and is to a large extent the result of contingency, rather than rational decisions. But already in the name natural language there lies a paradox, since every natural language that is spoken must inevitably be man-made, and therefore it will always carry a degree of artificiality.

It seems contrary to the very nature of human languages to think of them as being guided by a set of premeditated principles. Natural languages seem to have appeared more or less spontaneous in human history and went on to evolve organically after that. In fact, the true origin of the human capacity for language remains the subject of intense debate, albeit one that does not concern us too much when we want to unpack the concept of an ideal language.

But it is worth considering that due to the rational aspect that is innate to the human brain (Hauser and Watumull 2016), seemingly random variations in language are likely to be subject to ad hoc corrections for the sake of clarity and mnemotechnical purposes. In this light some authors have even proposed that there is no clear divide between natural and artificial languages. From this follows that one could construct a spectrum analysis of languages, to assess the level of naturalness (or artificiality) of any given language (Stria 2016).

A typical example of such a scale is a spectrum ranging from non-verbal animal communication to computer languages and ← notation schemes as shown below.

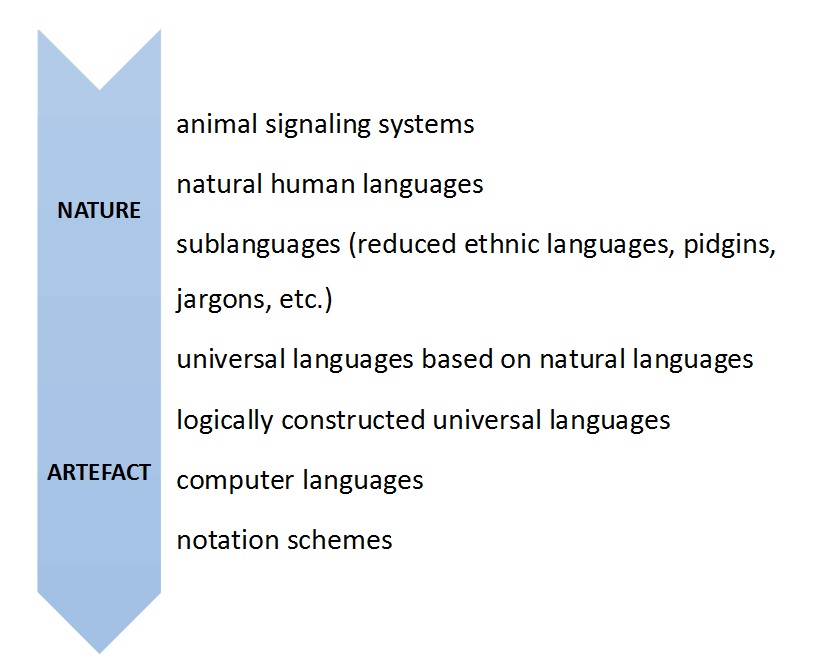
An ideal language can arguably be associated with what are called ‘logically constructed universal languages’ in this scale. To test this hypothesis, we will explore the historical examples of projects that aimed to produce an ideal language, starting with biblical references to the problem of the multiplicity of languages among humans to recent developments in computer science.

[top of entry]

2.3 Key components of ideal language

Consider that the very notion of an ideal language implies that it is unlikely to evolve naturally. Producing one would require a wilful act involving a rational plan or an imposed structure. Many religious interpretations allege that such a language did exist at a certain point in history, but that it was lost due to a cataclysmic event or some form of divine retribution. However, nothing in documented history points in that direction. Indeed, one could argue that if such a language would have existed, it would — by the sheer power of its persuasion and effectiveness — have begun to outcompete any other language it met. But no such thing has happened. Then how can an ideal language be identified and distinguished from natural languages?

Many definitions have been asserted concerning the concept of language. Some of them focus on it as a key feature of humans as a species: “Language is a purely human and non-instinctive method of communicating ideas, emotions and desires by means of voluntarily produced symbols” (Sapir 1921, 7). Others emphasize the social aspect of language: “A language is a system of arbitrary vocal symbols by means of which a social group cooperates” (Bloch and Trager 1942, 5). Still others focus on structural aspects: “From now on I will consider a language to be a set (finite or infinite) of sentences, each finite in length and constructed out of a finite set of elements” (Chomsky 1957, 2).

For the purpose of exploring the concept of an ideal language however, it would appear convenient to favour a definition that links the structural aspects of language with its ability to convey meaning: "A language consists of symbols that convey meaning, plus rules for combining those symbols, that can be used to generate an infinite variety of messages" (Weiten 2013, 318).

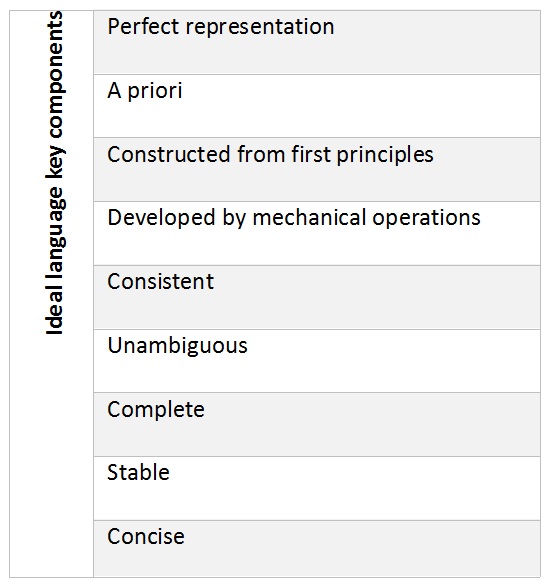
A broad definition of language is always arbitrary up to a point, as this is often the case with definitions of such complex and relatively impalpable phenomena. For our understanding of the concept of an ideal language, we decided to single out this last definition. The fact that it connects symbols with meaning through the mediation of a fixed set of rules, allows us to explore the concept of an ideal language more profoundly. For if we allow language to be understood as the permutation of a finite number of concepts within a fixed set of rules, we can imagine that it is possible to devise an ideal way of doing so. This would mean that a language could be constructed from first principles to transfer meaning from one subject to another in an unambiguous, consistent, concise and complete way. Such a language would qualify as an ideal language. The key components of such a language are summarised in table 1.

 

Table 1: Perfect language, summary of key components

[top of entry]

2.4 Knowledge organization systems (KOS) and ideal language

As we have indicated above, an ideal language will function as a system that both defines and organises unambiguous concepts. It shares these properties with most knowledge organization systems. To understand the similarities between KOSs and the search for an ideal language, we must first unpack the basic meaning of KO and KOS a bit further. As it has been asserted by Hjørland (2008), KO can be interpreted in a broad or in a narrow sense. In the narrow sense it revolves around practical organizing activities — like document descriptions, indexing and → classification — as they are generally dealt with in → library and information science (LIS). In the broader sense KO is about a large spectrum of historical, sociological and epistemological issues that range from the division of labour in an industrialised economy to the general organization of media in society. What defines it are its preoccupation with the production, organization and dissemination of knowledge.

An ideal language combines elements from both the narrow and the broad view of KO. They can for instance be a practical solution to the problems of knowledge organization, since they deal with the classification of concepts and additionally establish links between those concepts in a systematic manner. Apart from that, the historic attempts to create an ideal language have always been very much a part of the needs and characteristics of the historic and social context that surrounded them. But rather than merely being instrumental in facing the challenges of their day, ideal languages have attempted to overcome them by uncovering universals that would prove to solve the issue in every possible future age.

KOSs (like classification systems, thesauri and ontologies) can essentially be considered to be systems organizing concepts and linking them together through semantic relations (Hjørland 2009). Historically, ideal languages are the forerunners to this principle. With their commitment to unambiguousness, ideal languages have inspired the designers of the first → thesauri. The introduction to the well-known English-language thesaurus, created at the start of the nineteenth century by Peter Mark Roget (1805), contains explicit references to the ideas of Bacon [4], Descartes and Leibniz about the possibility of constructing an ideal language for the systematisation of human knowledge (Lyons 1977). However, the first thesauri were marketed for the much more modest purpose of assisting writers with their literary compositions. In the 1970’s The World Science Information System known as UNISIST defines a thesaurus as a terminological control device, used to translate natural language to the much more constrained “system language” used for library indexing (Foskett 1980). Overall, thesauri serve the purpose of providing a map of a given field of knowledge, indicating how concepts are related to one another and putting them in a hierarchical relationship. To accomplish this, a thesaurus aims to provide a standard vocabulary that can be applied to a given subject field and provides links to possible synonyms and other related terms like broader or narrower ones.

The level of standardization of concepts that we find in thesauri, is also a prerequisite for the construction of an ideal language. But it is not sufficient and must be complemented by a system that allows those concepts to be combined in ways that do more than just uniformize the terms involved. An ideal language aims to represent true knowledge and even allow its users to discover new truths through the internal logic of the system. To accomplish this, an additional system is needed that allows for the discovery of meaningful combinations within the standard vocabulary. This way the resulting structure will not just be a rendering of knowledge, but a generative system of discovery. Here the ambitions of ideal language surpass those of KOS. In KOSs the element that comes closest to this kind of intellectual dynamic within an information system, is the capacity of an indexing language to produce rules for combining the terms that are used in an index. But when we draw this analogy we must consider that what is indexed in an indexing language generally points to topics and features related to → documents, not universals.

But not all scholars of LIS subscribe to this view of indexing languages as being the mere passive representations of scientific progress. To understand this it is important to distinguish between two distinct ways to conceive a system of knowledge: One is that of a closed system that already contains everything there is to know about a given subject, and the other is that of a dynamical continuum of knowledge that is at any given time prone to changes of the existing body of knowledge, and where new elements can be added (or earlier elements subtracted) at any given time. In his Philosophy of library classification, Siyali Ramamrita Ranganathan points out that classical approaches to classification that are based on an enumerative scheme, fall short when it comes to represent this dynamic process:

An enumerative scheme with a superficial foundation can be suitable and even economical for a closed system of knowledge [...] What distinguishes the universe of current knowledge is that it is a dynamical continuum. It is ever growing; new branches may stem from any of its infinity of points at any time; they are unknowable at present. They cannot therefore be enumerated here and now; nor can they be anticipated, their filiations can be determined only after they appear. (Ranganathan 1989, 87)

In the view of Ranganathan it is by faceted classification that a KOS can keep up with an ever changing and growing body of scientific knowledge. Furthermore, this pioneering scholar of library science considered faceted classification to be to be a tool for the discovery of additional truths by exploring its combinatory possibilities. This view suggests that classification would no longer remain a mere reflection of the growth of scientific knowledge, but an active force in its proceedings. In doing so he attributes a priori value to his five basic facets (personality, material, energy, space and time). This position raises many questions. Ranganathans thinking on faceted classification has been discussed by Francis Miksa (1998) and Birger Hjørland (2013).

Indexing languages provide a means to mediate between the mind of the users and the information that is stored in a particular system (Mooers 1985). They can present themselves in many forms and involve the indexing of information in free-text-systems or in traditional classification systems that can be either enumerated or faceted. Again, ideal languages contain elements that are akin to the principle of indexing languages in KOSs, but project them to a new level. This is because the mechanism for navigating and combining concepts in an ideal language is not merely there for convenience, but out of logical necessity.

Because of this ambition, one can argue that an ideal language has much in common with a specific instance of a formal ontology. What do we mean by this? In KO, ontologies are considered to be the semantic systems that can boast the highest level of semantic richness (Bergman 2007). To understand what they encompass, we must consider that there are two ways of understanding the concept of ontology. In the first, more metaphysical interpretation, an ontology is a term that describes the study of what there is (Hofweber 2017). The second use of the word is of a more technical nature and sees it as a formal specification of a conceptualization (Gruber 1993). In this capacity an ontology is no longer a singular term, but a practical apparatus, designed to function under a given set of circumstances. One could argue at this point that under these conditions, an ontology loses its main purpose which is the search for universals. By allowing multiple ontologies, with no clear way to distinguish the good from the bad ones, it is easy to slide into an idealistic mindset where the very idea of the existence of universals is dismissed (Smith 2004). An ideal language ontology firmly resists falling under this category, and rather aims to marry the formal aspect of the second use of ontology, with the metaphysical claims of the first.

In the KO literature four different philosophical approaches have been distinguished. These are: empiricism, historicism, pragmatism and rationalism (Hjørland 2017). The project of creating an ideal language applies almost exclusively to the last one. The other approaches all contain a form of contingency that is alien to the ambitions of an ideal language. Furthermore, it is implied that an ideal language can be constructed independent of the environment in which they arose.

But even if the structure of an ideal language is — as it is claimed by its proponents — unaffected by historical or other human contingencies, it does not neglect to reflect the fundamental structure of the world. Therefore ideal languages fit a characterization of KO that states that it organizes conceptual knowledge in principles or theories as opposed to how knowledge may be organised in actual society (Whitley 1984; Hjørland 2016). Indeed, most ideal language projects promise to provide some form of rational clarification of the concepts in the real world, rather than just describing its phenomena. Any social dimension an ideal language might have would only become apparent after they are introduced. For example, in the impact they have on societies by eliminating misunderstandings.

[top of entry]

2.5 The Tower of Babel and the monogenetic hypothesis

As mentioned earlier it is by no means our intention to give a complete account of all the attempts that were made throughout history to construct an ideal language. A much more thorough overview for the search for the perfect language — that served as a guide for the summary below — can be found in the book by the same title by Umberto Eco (1995). Instead we will discuss four instances where the idea of an ideal language emerged: The biblical myth of the Tower of Babel, The Ars Magna of Ramon Llull at the turn of the 14th century, the Lingua Generalis of Gottfried Wilhelm Leibniz at the turn of the 18th century and the case of machine languages in the early 21st century.

Notwithstanding the complete absence of any historical factual basis, the story of the Tower of Babel has for centuries deeply influenced Western thought on the topic of the diversity of languages in the world. More specifically, it has fuelled the idea that the multitude of languages that is spoken around the world is synonymous with confusion. The tower itself is of course a mythical construction that is mentioned in Genesis 11:1-9 of the Hebrew Bible. According to the story, all people spoke only one language when they settled themselves in the land of Shinar, after they had escaped the great flood. There they started the construction of a tall building: “Come, let us build ourselves a city, with a tower that reaches to the heavens, so that we may make a name for ourselves” (Genesis n.d.). But God, who witnessed this, decided to interfere with their plans. Not only did he scatter the people over the face of the earth, in addition he confused their language, so they would no longer be able to understand each other.

The story gives us an account of the origin of the diversity of languages that is very unrealistic and even antithetical to what science tells us about how the historic development of language probably came about. It is for instance very likely that the first languages that developed on earth were indeed natural languages. Nevertheless, thinkers like Jacques Derrida claimed that it tells us more about language, its meaning and the relationship between a common language and the completion of a great task:

The “tower of Babel” does not merely figure the irreducible multiplicity of tongues; it exhibits an incompletion, the impossibility of finishing, of totalizing, of saturating, of completing something on the order of edification, architectural construction, system and architectonics. (Derrida 1985, 191)

Two centuries before Derrida, Voltaire in his Dictionnaire philosophique coined the essence of the confusion that was caused by the events surrounding the tower as follows:

I do not know why it is said, in Genesis, that Babel signifies confusion, for, as I have already observed, ba answers to father in the Eastern languages, and bel signifies God. Babel means the city of God, the holy city. But it is incontestable that Babel means confusion, possibly because the architects were confounded after having raised their work to eighty-one thousand feet, perhaps, because the languages were then confounded, as from that time the Germans no longer understood the Chinese, although, according to the learned Bochart, it is clear that the Chinese is originally the same language as the High German. (Voltaire 1901, 374) [5]

Note that in this passage, Voltaire also points out that the name Babel refers to God himself [6]. So, the confusion appears to be present at the very outset of the story. An insight that is echoed by Derrida, who points out that without a clear understanding of its proper names, any hope of a clear translation between languages is lost.

This interpretation of the familiar myth hints at a profound problem that may undermine any attempt to mend the problem of the fragmentation of languages. It claims that any translation is essentially insufficient. Furthermore, the language that preceded the confusion of Babel does not necessarily have to be ideal. For the story to be consistent one would only have to assume that it was universally accepted. However, mere conjecture made based on a mythical story may prove to be very unstable ground for rejecting the possibility of (re)unifying languages altogether. A more rational approach to the problems of translation may prove to be more productive.

The fact that at present there does not exist a common language that allows all humans to communicate in an unambiguous way is undisputable. The answer to the question whether it is at all possible for such a language to exist at all is "unlikely", but the question remains open for debate. In the case of natural languages, the situation seems hopeless. The complexities and subtleties of natural languages make that there is always some room for interpretation about what is said or written. From this follows that the exact meaning of any expression in a natural language is never fully determined. Take for example the word chair: even though there is a broad consensus about what a chair might be and how it would look like, it is safe to say that when the word is used by one person, the corresponding idea will differ, however slightly, from the idea that is in the mind of the receiver. Now take the same word and assume that it is used in the context of people on death row, or in the setting of a business meeting. Both the exact meaning of the word and the spatiotemporal context make that natural languages are always in a state of flux and never fully determined.

Nevertheless, many attempts to find a shortcut through the forest of multiple languages were made in history. An important part of these efforts was related to the so-called monogenetic hypothesis. This hypothesis assumes that all languages originate from one single ancient language that at one point in the course of history was lost or became unintelligible to humans. For a long time, people tried to reconstruct this ‘language of Adam’ by carefully studying existing languages. But none of these attempts was very successful. In this context it is worth mentioning De vulgari eloquentia by Dante Alighieri (1265-1321) (1996). In this work the great Renaissance poet describes three stages in which the ancient languages were transformed into the languages we know today. Dante considered it his mission to reconstruct a more illustrious and clearer language from the debris of this ancient tongue. That language, however, would be a natural language and one that would be picked up by many because of its obvious qualities (Eco 1995).

[top of entry]

2.6 A priori philosophical languages

Another attempt in this respect that is worth mentioning is the search that was undertaken by John Wilkins. Wilkins was a 17th century Englishman and clergyman who published a book in 1668 titled: Essay towards a Real Character, and a Philosophical Language (Wilkins 1668). It developed into a complete project for constructing a universal language. His goal was to compose a language consisting of characters that would be understood by people from every nationality. This endeavour was a continuation of previous attempts to develop a rational language in the form of a Universal Character made by George Dalgarno (1626?-1687) and Cyprian Kinner (d. 1649), as it was pointed out by Hans G. Schulte-Albert (1974). Wilkins project balanced the ideas of a logically constructed grammar and a creative presentation of existing taxonomies (Emery 1948). Unfortunately, his invention would never make a big impact, but Wilkins himself will always be remembered as the founder of the British Royal Society. In literature his name lives on thanks to an essay by Jorge Luis Borges titled "The analytical Language of John Wilkins" (Borges 1988; Clauss 1982).

A dismissal of the monogenetic hypothesis — or at least folding to the idea that this language is forever irretrievably lost — does not necessarily mean that the project of forming a means of communication that is truly universal should be impossible. Many scholars from Francis Bacon to Comenius have contemplated a different approach. But it was the 17th century French philosopher René Descartes who formulated a clear, but by no means the first, approach to solving this in his correspondence with Marin Mersenne in November of 1629 (Descartes 2017). Reflecting on the idea of a universal translator Descartes stated that, although it would be conceivable to translate every isolated word of a language piece by piece (all you would need is a good dictionary), it would be far more difficult to learn an exotic grammar. Therefore, it would be easier to invent an intermediate grammar that is free from the irregularities of the natural languages. This language would be very basic and could be conceived as follows:

It was sufficient to establish a set of primitive names for actions (having synonyms in every language, in the sense that the French aimer has its synonym in the Greek philein), and the corresponding substantive might next be derived by adding to it an affix. From here a universal writing system might be derived in which each primitive name was assigned a number with which the corresponding terms in natural languages might be recovered. (Eco 1995, 216)

This relatively simple idea describes the essence of the entire rational approach to constructing an ideal language. What is needed to put this idea into practice, however, is the development of a philosophy that produces a finite set of fixed and distinct ideas that could subsequently be enumerated. These simple ideas could then be combined to generate more complex ideas, until they comprised every single thought the human mind could possibly entertain. The natural outcome of such an undertaking would be to produce a kind of mathematics of thought or an a priori philosophical language.

John Wilkins project, that was developed not long after Descartes, is akin to the ambitions of producing an a priori philosophical language. However, at the time Descartes and Wilkins reflected on these ideas a major attempt to accomplish the notion of an ideal language had already preceded them by many centuries, as we will show below in some detail.

But before we look at one of the first serious historic attempts to create an ideal a priori philosophical language, it is interesting to consider briefly the character of the opposite of the a priori languages, namely a posteriori languages. These languages are plentiful even today. One only has to consider the different symbolic systems that are used by musicians, electricians or chemists that aid them in communicating the intricacies of their respective activities. Like a priori languages, these languages are purposefully designed, but instead of being guided by a limited set of basic principles, their designs are dependent on a combination of elements that are drawn from existing languages, combined with a form of shorthand that emerged organically from concepts that are used regularly. Some of these constructed languages have even had a defining influence on the formation of the disciplines they emerged from. This has definitely been the case for chemistry, as was shown convincingly by David Bawden:

However, particularly to someone like myself who studied chemistry, it is interesting to reflect on the extent to which information representation and communication has gone hand-in-hand with the development of concepts and theories in chemistry, so that it is difficult to tell where the one ends and the other begins. (Bawden 2017)

This observation represents a clear example of a mechanism that operates as the inverse of a priori languages.

[top of entry]

3. Ideal languages in the Middle Ages and early Modern period

3.1 Ramon Llull and the Ars Magna

3.1.1 A topical outline of Llullian combinatorics

Dealings with other cultures and the difficulties that these things bring about, were often the direct cause that would spark the interest for the search of a shared, true language. Ramon Llull lived between 1232 and 1316 on the island of Majorca (Hillgarth 1971). In his time Majorca lay on the crossroads between the Christian, Jewish and Arab cultures. After receiving a vision in 1263 he dismissed his previous worldly life and devoted himself to Christianity and the conversion of Muslims to Christendom. In nine years of study that followed this event, he accumulated a profound knowledge of both the Arabic language and philosophy, as well as Christian philosophy and theology. He familiarised himself, among other things, with the Logic of al-Ghazzali which would become a major influence on his later work. For example, the representation of philosophical terms by the letters of the alphabet became a key part of Llull’s own algebraic logic. This way of thinking facilitated his use of the mechanical operations that where induced by his firm personal conviction that there are only a limited set of undeniable truths in any particular field of knowledge. He also drew inspiration from Augustine. In particular the text De Trinitate, a work that was inspired by the philosophy of Plotinus. From the Jewish tradition Llull drew on the ideas of the kabbalists. A key element of his methodology lies in the application of combinatorial principles to categorical elements. Combinatorics have been a major part of the temurah tradition in the kabbalah. Already in the Sefer Yetzirah, dating back to a period between the Second and the Sixth centuries, a description of factorial reasoning can be found (Eco 1995).

Llull wanted the conversion of Muslims by means of peaceful persuasion. Even though he did become an advocate for an armed crusade late in his life, this did not reflect on the vision he proclaimed during the rest of his life.

In his great contest for the conversion of the world Llulls’s arms were those of intellect and love. His was one of those rare minds, able to assimilate, in their search of a synthesis, the truths of different and opposing schools. (Hillgarth 1971)

Llull set of on a course that would lead him to towards the Art of finding Truth. In it Llull attempts to make a synthesis of Christian and Arabic thought. Around 1274 he published his first findings. These would grow into a lifelong endeavour that would be developed further into his Ars generalis ultima in 1308 (Llull 1970). Llull attempted to appeal to the fact that all the major religions in the region were in some way based on similar neo-platonic ideas. His art would reflect key elements of neo-platonism, in the way that they could serve as a common ground for every educated person to be able to agree on. Even though there are many dimensions of Llull’s work that are fundamentally spiritual by nature, his work displays distinct marks of a rationalist worldview.

This rationalism is most explicit in his Ars combinatoria. From his study of the kabbalah came the knowledge that for a given number of elements n (for example the letters in the alphabet), there can be only a limited number of arrangements in which these elements can appear, a number that can be found by calculating the factorial n!.

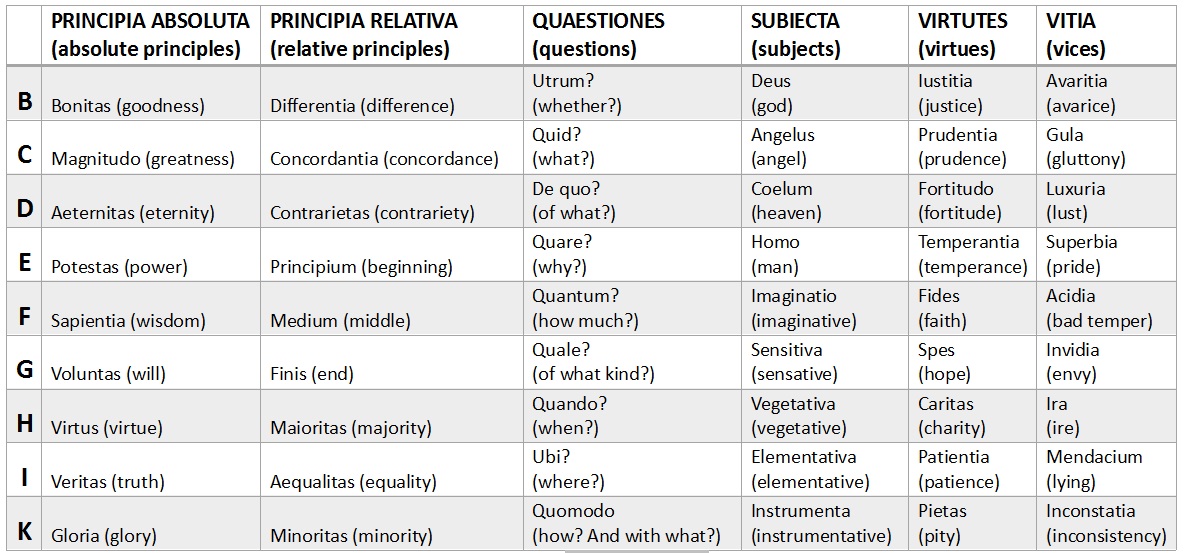
Llull uses a → notational system of nine letters (B, C, D, E, F, G, H, I, K) that can represent any of 54 predicates, grouped in six distinct columns in what is called the Ars brevis (table 2).

 

Table 2: The alphabet of the Ars Brevis (adaptation based on Bonner 2007b)

The first two columns deal with principia or principles and allow for the deduction of syllogisms. The first column contains absolute or godly principles like "goodness" or "truth". These principles can be combined amongst themselves to result in many godly properties. The order in which they appear when performing this operation is irrelevant. For example, it is possible to combine goodness (Bonitas) with greatness (Magnitudo) to read "goodness is great", but this has the same value as "greatness is good". Self-predications (ex. "goodness is good") are not allowed in the system. Under these rules it is possible to get 9! / (9-2)! = 72 possible expressions by combining the absolute principles. This is represented in the combinatory wheel shown in figure 2. The results of these combinations are expressions that possess value as they are derived from the system. If, for example, we want to demonstrate that in the divine sphere goodness is great, we can argue that all that is enhanced by greatness is also great. So, when goodness is enhanced by greatness, goodness will be great.

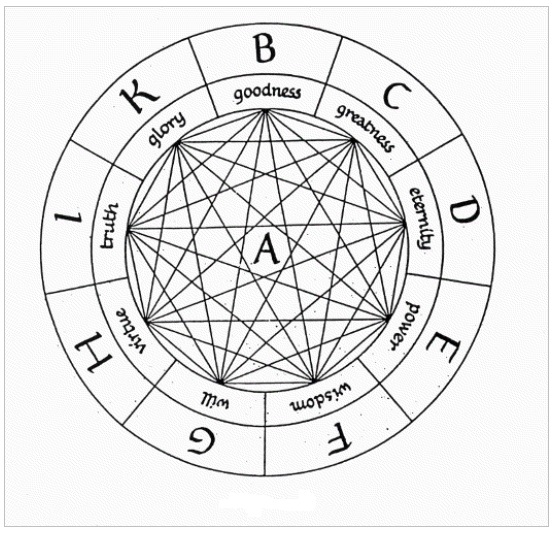
Next, Llull combines the elements of the second column. In doing so he sorts the nine relational principles found there in three groups of three, represented in figure 3 by the triangles in the centre. The concentric circles show the areas where these principles can be applied. For example, "beginning" can apply to a cause, a quantity or a time and "difference" can apply to the difference between the sensual and the intellectual.

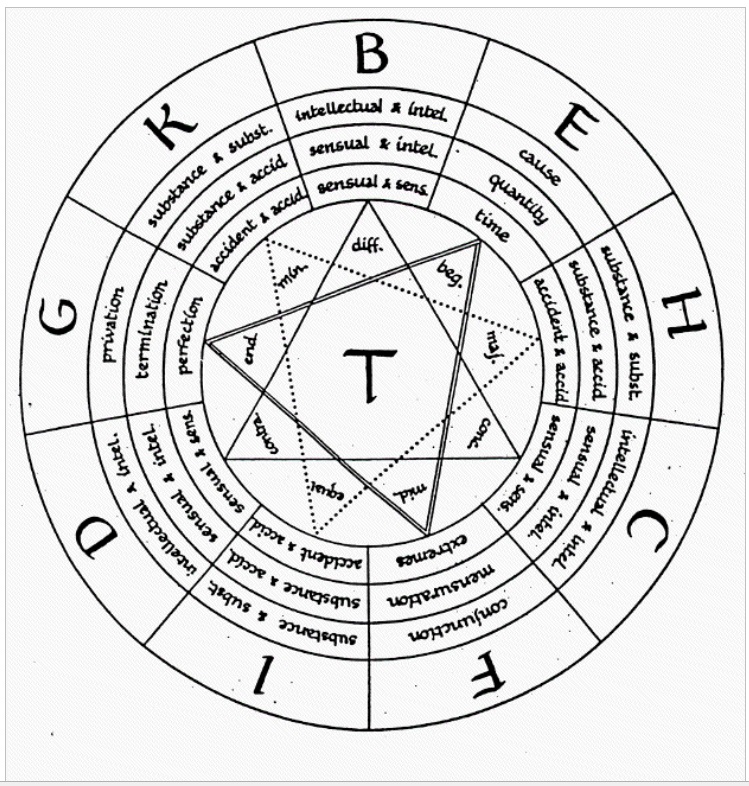
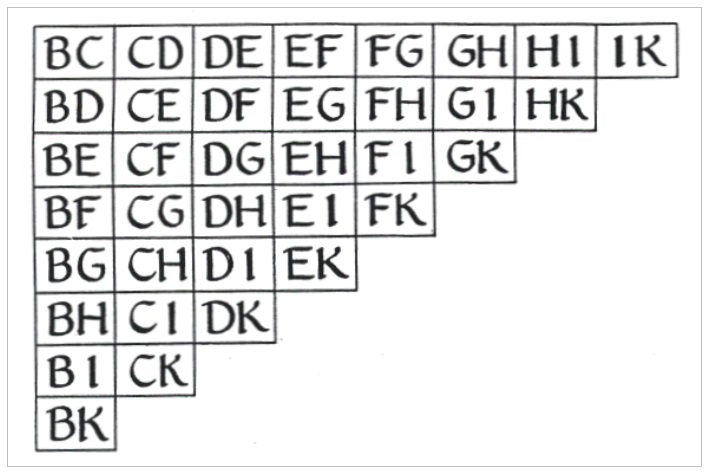
The next figure combines the first two (see figure 4). The combination BC for example implies four concepts: "goodness" and "greatness" (from table 2) and "difference" and "concordance" (from figure 3). This way a phrase like “Goodness has difference and concordance” can be analysed (Bonner 2007). When following the half matrix (half, because BC is in Llull’s system identical to CB) in this way, Llull wanted to explore all possible combinations of his system. It is precisely this indication of completeness that makes his art general and, in that capacity, also ideal.

To expand the language Llull allowed the binary combinations in figure 4 to include the questions from column four, corresponding with the given letters. BC now stands for one statement ("goodness is great"), and two questions about this statement ("whether goodness is great?" And "what is great goodness?"). Together with the corresponding relative principles (difference and concordance) this makes a total of 12 propositions and 24 questions from just one binary pair.

This way, the full table generates 432 propositions and 864 questions. (In theory at least, because according to the rules of the art, there are 10 limitations that need to be considered that rely on theological foundations.) To integrate this third column clearly in the system, Llull and his medieval followers constructed small dynamic devices made of three concentric circles containing the nine letters that where cut out of parchment and then tied together with a string. By turning them, this device showed the 84 possible groups of 3 letters that form the Ars magna generalis. Table 3 shows just seven of the Ars brevis and expands them further in each column.

 

Table 3: Ternary relations, based on the fourth figure (Bonner 2007b)

Notice that the letter T is introduced in this table. T should be understood as a mere placeholder separating the first from the second part of the expression: All letters before the T stand for absolute principles of the first column. Also, the first letter indicates to the corresponding question from column three. The part after T designates relative principles from column two. Keeping this in mind, the expression B T B D can be read as the phrase “Whether goodness contains in itself difference and contrariety” (Bonner 2007b).

When we study these combinations, it will soon be clear that the permutations sometimes produce nonsensical sentences. Some conclusions even outright contradict other formulations. Part of the ‘art’ was to also contemplate on these contradictions in an attempt to arrive at the correct interpretation.

[top of entry]

3.1.2 The Arbor scientiae

By 1295 and 1296 Llull had developed the idea of the Arbor scientiae. This tree of science is sometimes considered to be an encyclopaedic framework for the Ars magna (Lima 2011), but it would arguably be more accurate to state that it acts as an elaborate justification for the structured classification of different fields of knowledge. The representation of the different scientific subject as branches of a tree, is a powerful image that was already in use long before Llull wrote it down. Indeed, the neoplatonist philosopher Porphyry, who lived from c. 234 to c. 305 AD, famously used this metaphor in what is now known as the Porphyrian tree. His tree was used as an introduction to Aristotle’s classification of categories. The sixth century philosopher Boethius carried the image into the Middle Ages through his translation of Porphyry’s principal work Isagoge from Greek to Latin, in what would become a standard philosophical logic textbook in the Middle Ages (Gracia and Newton 2016). It is only recently that other images have begun to compete seriously with this classical example (Mazzocchi 2013).

With this systematic representation of how human knowledge is organised, Llull produced a complex mapping of all science, visualised as a total of sixteen trees. The overall structure of this small “grove” of trees can be summarised as follows:

The first fourteen trees each represent one grade of a “scale of being,” which is the first and most fundamental hierarchy of the system, and which comprises of trees of the Elements, Plants, the Senses, Imagination, Man, Morality, Government, (Christian) Theology, the Heavens, Angels, Eschatology, the Virgin Mary, Christ and God. Two additional “meta-trees” are concerned with parables and proverbs related to the first fourteen trees as well as with a lengthy but methodical application of term combinations and principles to a wide variety of questions”. (Walker 1996, 200) [7]

A tree representing with its branches all the other trees that exist in this imagined grove of trees is show in figure 5. Each tree was itself divided into several parts (trunk, roots, fruit, etc.) that produced a further subdivision that ranged from one to 137 terms. The roots of these trees are made up of the absolute and relative principles that we encountered in the Ars Brevis. The trunks unify these principles out of which branches grow that represent new elements. From the trunk of the elemental tree, for example, grow the four basic elements water, earth, air and fire in the form of large branches (figure 6). The branches sprout smaller branches and flowers to represent ever more specific terms that are related to the main categories. Although the structure of the trees is logically sound, it does not qualify as a strict hierarchical knowledge organization system. Llull applies the same combinatorical principles in his tree of science, as those that are present in the Ars magna. Therefore his system qualifies more as a faceted system of knowledge classification (Walker 1996).

[top of entry]

3.1.3 Llull’s legacy

It is clear, when considering these obvious shortcomings, that it was highly doubtful that the Ars Magna had the ability to develop into the universal language for communicating clear knowledge and narrowing the cultural gap between civilisations.

Llull’s theories managed to accumulate a sizeable following, even long after his death. The popularity of his approach, was not necessarily diminished by its lack of accessibility. Its real strength lay in the method he had developed. The execution of mechanical, combinatory operations could in a way act as a substitute for reasoning. From this perspective the essence of reasoning hinges on the destruction and reconstruction of connections between attributes. The mechanical aspect of his invention is illustrated by the objects (three moving concentric circles, held together by a piece of rope) that were made to help contemplating the true meaning of the triplets. But the process of mental exploration does not end with the outcome of a random query of the allowed combinations. What the Ars Magna ultimately shows, is that the development of meaningful statements requires more than just a rational argument.

Methodologically it bears some resemblance to the → Colon Classification of S.R. Ranganathan (1990), in that it used the combination of concepts to describe all subjects. But rather than being a bibliographical information system meant for retrieving records, Llull’s system was constructed for the discussion of philosophical problems in a systematic, mechanical and complete way (Walker 1996).

Today, Llull is even credited by some for being a forerunner of computation theory and even that his system — that is based on logic and combinatoric principles — can be considered an early precursor of information science (Bonner 2007a; Knuth 2006).

[top of entry]

3.2 Leibniz and the Lingua Generalis

The philosopher, mathematician, diplomat and librarian Gottfried Wilhelm Leibniz (1646-1716) devoted a large part of his life to the goal of producing a clear and noble language to facilitate the flow of knowledge throughout the world. Just like Ramon Llull before him, he was convinced that if we could find a clear way of formulating human thought, this would open the possibility to establish peace between nations. Indeed, his life's work consisted of four different parts: (1) identifying a system of primitives that can be arranged in a general encyclopaedia, (2) the development of an ideal grammar, (3) the formalization of a collection of rules for the pronounciation of the used characters, and (4) the creation of a lexicon of characters that would lend themselves to calculations that would help in determining which are true statements.

By the end of his life, Leibniz had largely abandoned the first three proposals and committed himself solely to the fourth one. Leibniz was no longer interested in new languages like the one John Wilkins advocated, even though he was familiar with it and was impressed by the attempt. He concluded that it was impossible to find a connection between existing languages. As a consequence, it would also be impossible to reconstruct the language of Adam. From his metaphysical theory of the monads, he took the idea that every individual must necessarily have a unique outlook on the world. In this light it would be impossible to unite all these different points of view into one linguistic framework. Variance was the essence of life in the cosmos for Leibniz. Based from a religious ideal of world peace, he did not think that this could be achieved by the desire for every human to speak the same language. In his mind, it was science that was best suited to attain that goal. The universal language he wished to develop was subsequently a scientific tool that would help to clarify truth.

[top of entry]

3.2.1 Coding language

Leibniz was inspired by Llull’s ars combinatoria and developed a combinatory system of his own, in an essay titled Dissertatio de arte combinatoria, early on in his career (Leibniz 1666). But even though he found inspiration in Llull’s approach, he did not see the value in the limitations Llull had set to the art that were inspired by theological assumptions.

But he was fascinated by a problem that was forwarded by Marin Mersenne [8]. The problem went as follows: how many possible words can be formed by the 24 letters of the alphabet that was in use at the time? The meaning of this was to figure out how many truths could be expressed in writing. The longest word that was known to him had 31 letters. In the 24-letter alphabet there could be a maximum of 24³¹ 31-letter words. But why would 31 letters be the limit? One word could in theory fill out a whole book. Leibniz contemplated that if we assumed that if a man read 100 pages containing 1000 letters per day and would live for 1000 years, during his long life he would amass a total of 3.65*10¹² signs of truths, lies and meaningless expressions.

Confronted with this extraordinary large number, Leibniz realised that the possibilities far outweighed any human capacity. The answer should therefore be found elsewhere. He proposed that the total number of all possible meaningful expressions would be finite. This would be revealed in the infinite number of possible combinations of letters in words of all possible lengths by the emergence of repetitions.

Leibniz conceived his Lingua Generalis in 1678. In his philosophy he managed to reduce the total of human knowledge to many singular ideas. Each idea was to correspond with a certain number. Next, he thought of a system of transcription where consonants were represented by natural numbers, and vowels stood for powers of ten. So, in his system the number 81374 for example, would stand for the word mubodilefa (see table 4). The focus in this system is the grouping of the consonants and vowels in pairs. How these pairs are ultimately ordered is not important, so "81374" could also be transcribed as bodifalemu.

 

Table 4: Lingua Generalis

These efforts in constructing a language that could be plotted out entirely using a numeric code, would indicate that Leibniz too — like Wilkins and Dalgarno [9] before him — was trying to develop an entirely new and artificial language. But it must be pointed out that Leibniz also devoted himself to the construction of a simplified version of Latin that was destined to be spoken. The efforts resembled the Latino Sine Flexione that was invented more than two hundred years later by the Italian mathematician Giuseppe Peano (1858-1932) (Kennedy 2002).

But the significance of the Lingua Generalis was in its method. His way of working foreshadowed the system of replacing signs with numbers that is known as Gödel numbering, after its inventor. Gödel used this technique of replacing logical notation by numbers based on prime factorization to prove his incompleteness theorem. Leibniz also uses primes to divide expressions up into smaller formal parts. This process is repeated until the expression can no longer be divided any further. By counting the number of factors after applying integer factorization to a given expression Leibniz was able to establish a hierarchy to the complexity to the expression [10].

In a series of papers written in April 1679, Leibniz develops the idea of assigning natural numbers to the subject and predicate of a proposition, so that the original proposition can be reconstructed by just looking at the numbers. At first, he was optimistic about the possibility to use these principles to determine the truth of any proposition. Later he boiled this ambition down to the more modest goal of determining whether a syllogism is logically valid (Lenzen 2017):

For example, since ‘man’ is ‘rational animal’, if the number of ‘animal’, a, is 2, and the number of ‘rational’, r, is 3, then the number of ‘man’, m, will be the same as a*r, in this example 2*3 or 6. (Lenzen 2017)

To verify whether a given proposition is true, one had to establish whether the ratio of subject to predicate is a whole number. If for example the number 10 was attributed to monkey, we should be able to determine that the sentences ‘all men are monkeys’ and ‘all monkeys are men’ are incorrect. This would appear to be the case, since neither 6/10 or 10/6 are whole numbers (Eco 1995).

[top of entry]

3.2.2 Leibniz’s Legacy

We can see that Leibniz often resorts to elementary terms like entity, substance and attributes that remind us of the classical Aristotelian categories. Even though Leibniz had high expectations of his conception, by the end of his life he had to admit that the initial goals seemed increasingly elusive. At a higher age he even started to doubt that a definitive list of primitives would ever be found — a fact that he contributed to the changeability of men and the world we live in — and that this was not solely a matter of convention, considering that defining these primitives would have to precede the development of the lingua characteristica. In other words: the concepts that were meant to be expressed by the system would have to emerge out of a calculus that needed these very concepts to work. It seems like his project had arrived at an impasse.

After Leibniz' hopes of constructing an ideal language had evaporated, he shifted his attention to pursuing his dream of building a universal encyclopaedia. Such an encyclopaedia would be a practical instrument that would offer every literate person access to knowledge. Building it could open a possibility to achieve, although with different means, the same ultimate goal he had in mind for ideal language: peace between nations. Just a few decades after Leibniz' death, Diderot and d’Alembert started to work on such an encyclopaedia. Leibniz realized early on the importance of having a good index. One that would allow the reader to navigate the vast bulk of knowledge present in the work, as the encyclopaedia grew. Constructing a clever index would retain certain elements that are reminiscent of the ingenuity of the ideal language project (formal, flexible, logically sound), but stripped of its aspirations.

Perhaps the spirit of the more ambitious projects of Leibniz, endeavours that during his lifetime have either failed or where left unfinished, live on in a more modest way using indexes. These indexes may even be the precursors of the modern → hyperlink.

[top of entry]

4. Ideal language in the modern world

4.1 The ambitions of logical positivism

Can artificial and formalized languages overcome the shortcomings of natural languages? This was a question that preoccupied much of Western philosophy in the 20th century. The conviction that creating a perfect formal language is indeed attainable was held by many scientists, mathematicians and philosophers at the beginning of the 20th century. Emblematic of this sentiment was a program, which was forwarded by mathematician David Hilbert in the 1920’s (Zach 2007). Hilbert recognized that the foundations of mathematics still needed to be secured, and therefore called upon the scientific community of his time to mend the problem. This solution would include a complete formalization of all mathematics, proofs of completeness and consistency, conservation and decidability. These elements certainly share a similarity with the aspirations of the historical proponents of an ideal language. However, the object of this new strife to perfection, namely mathematics, had drifted very far from what we would generally consider a language. It is also not driven as much by a social agenda, as was the case with Llull and Leibniz, but seemed to be only concerned with pure science. What modern rationalism did have in common with its historic predecessors, was the notion that the construction of a complete and unambiguous system in which all human concepts would be perfectly represented with absolute transparency, was indeed possible.

Soon after the ambitions of Hilbert and his sympathisers were made public, some profound difficulties arose. Strangely enough, these difficulties emerged from the ranks of the most committed advocates of the new ideal language movement. Let us examine the significance of this break in more detail and consider the consequences it has for ideal language construction.

Is it possible to construct a perfect formal system? This is by no means certain, but it has been the conviction of many philosophers and mathematicians in the 20th century that such an ideal formal system could and would eventually be discovered. Indeed, much of the work of what is typically described as analytic philosophy during that period is linked to this project. Important thinkers like Gottlob Frege, G.E. Moore, Bertrand Russell and a young Ludwig Wittgenstein were involved in conceiving a firm theoretical framework of mathematics and logic, that would provide an irrefutable foundation to mathematical and scientific thought.

This project was incorporated, developed and even turned into a veritable intellectual program by the members of the Vienna Circle. The circle was founded around 1925 by the physicist and philosopher Moritz Schlick. Its members included the philosophers Rudolf Carnap and Otto Neurath, the logician Kurt Gödel and the physicist Philipp Frank. They also had many affiliates all over the Western world [11]. The Vienna Circle formed a school of Western philosophy that is known as logical positivism. Philosophy for them was first and foremost a project that held the task of clarifying certain expressions, without having a definite subject matter of its own. From this follows that knowledge and meaning can only have relevance if they are reducible to a formal system that governs the rules of thought. Several attempts were made to form such a system. A famous and monumental attempt to found mathematics in so-called first-order (or propositional) logic was Principia mathematica by Bertrand Russell and Alfred North Whitehead. In this three-volume work the authors attempted to solve a problem that was discovered by Russell in 1901 [12], that was present in earlier attempts to provide a foundation to logic. The Principia, however, failed in solving the problem. During the decades following the publication of the Principia, several problems would arise that would fatally injure the project. We will discuss a few of the major ones.

[top of entry]

4.1.1 The limits of logic

First let us start in the early 1930’s when Alfred Tarski famously argued that there are in fact two different languages in play in formal systems whenever we wish to express truths: namely an object language (the language we use to talk of the things in the world) and the metalanguage (an artificial language used to analyse or describe elements of the object language itself) (Kirkham 1992). This is important when considering the possibility of an ideal language. Consider a paradoxical statement like “this sentence is false” [13]. In first-order subject-predicate logic the paradox cannot be eliminated, since the system is semantically closed, i.e. it cannot contain its own truth predicates. Therefore, a metalanguage is introduced that can deliver a truth predicate to the object language. But this means that the truth of any expression in a formal language is always in a way conventionalized.

At the same time when Tarski started working on the problem of truth in formalized languages, another logician, named Kurt Gödel, formulated his incompleteness theorem, which had even wider implications. His theorem stated that any axiomatic system that can produce the arithmetic of natural numbers that is consistent, cannot be complete. And secondly that the consistency of the axioms cannot be proven in the system [14]. This theorem questions the capacity of even the most fundamental axiomatic systems — like Zermelo-Fraenkel set theory — to be perfect. It does not only apply to predicate systems, but it is equally damaging for second- or higher order logic systems. For many, this theoretical development meant the end of the dream of logical positivism for attaining indubitable knowledge [15]. This constitutes the second problem we wanted to consider. It is, however, worth mentioning that Gödel himself never abandoned the possibility of the construction of some higher form of logic that would bypass the problem.

Thirdly, in 1936 — building on the work of Gödel — Alan Turing wrote a paper (Turing 1938) that would deliver a crippling blow to the possibility of constructing a perfect formal system. In that year Turing arrived at what is known today as the problem of uncomputability, which was his answer to the Entscheidungsproblem. This fundamental problem in mathematics was introduced by David Hilbert as a part of his famous program. Hilbert had asked the mathematical community to create an algorithm that would be able to evaluate whether a statement in first-order logic would be universally valid or not. Turing proved that such an algorithm could never be found.

He came to this conclusion when he invented the principle of what would later be known as a Turing-Machine. This theoretical machine was the realisation of a mathematical model of computation that can simulate the computations of any computer algorithm. Every modern computer that has ever been built, is a working Turing-Machine.

With this invention arose a fourth problem: Consider that some programs that can be written for such a machine would keep on running indefinitely [16]. The problem is that it is not always clear, whether a program will finish its program in a finite number of steps, or whether it will keep on running the program forever. The problem of determining what a given program will eventually do, is known as the halting problem. In other words, would it be possible to build a set of instructions that could determine, for any given program, whether it would eventually stop. Turing proved that such a solution could never be found [17]. This conclusion had far-reaching consequences:

Turing’s discovery was that any reasonably strong mathematical theory was undecidable, that is, had an incomputable set of theorems. In particular, Turing had a proof of what became known as Church’s Theorem, telling us that there is no computer program for testing a statement in natural language for logical validity. (Cooper 2012, 778)

These four objections to the notion of the infallibility of formal languages are intimately connected to the idea of an ideal language. They imply that the construction of an ideal language in the strict sense, turns out to be an unobtainable goal. Not only do they confirm that an ideal language has never existed, they illustrate that it would be utterly impossible to ever build one. This is of course if such an ideal language would be closely related to formal languages such as mathematical logic or computer programming. We have seen that all major historic attempts indeed share those similarities. This would suggest that the search for an ideal language is like building castles in the sky and that the dream of logical positivism would forever remain unattainable. The only hope to revive it would be to extend first-order logic with a logic of a higher order, or to discover an even more exotic solution.

[top of entry]

4.1.2 The language of the mind

But there may be another way in which the search for an ideal language might still be conceivable. In 1975, Jerry Fodor argued that mental representations do in fact have a linguistic structure. This concept became known as the language of thought-hypothesis or LOTH (Fodor 1978). In this view, a representational system is said to have a linguistic structure if it possesses both a combinatorial syntax and compositional semantics. This definition seems to fit most formal languages. The argument for LOTH can be summarised as follows:

In short, human beings can entertain an infinite number of unique thoughts. But since humans are finite creatures, they cannot possess an infinite number of unique atomic mental representations. Thus, they must possess a system that allows for [the?] construction of an infinite number of thoughts given only finite atomic parts. The only systems that can do that are systems that possess combinatorial syntax and compositional semantics. Thus, the system of mental representation must possess those features. (Katz 2017)

Stretching this view only a little bit further, one could argue that it may indeed be impossible to construct an ideal language as the function of an axiomatic system, but that it could be possible to develop a language that offers the best possible approximation of the language of the human mind.

But there are notable difficulties with the LOTH. Consider for example the problem of individuation of primitive symbols within the language. In other words: how can the supposed brain-states be represented clearly and unambiguously? In addition to this, there are the context-dependent properties of thought, that cannot be represented by a computer model. Also, there are significant indications provided by cognitive science that thinking takes place in mental images that do not have a linguistic structure. All of these objections may prove to be fatal to the hypothesis, and thus diminish the possibility of an ideal language of mind.

[top of entry]

4.1.3 Language by machines

Perhaps, the last refuge for the hope of realizing an ideal language rests not with humans, but with machines. Needless to say, that this is highly speculative, even though it carries with it some unique prospects.

Research on Artificial Intelligence (AI) has proposed that for machines to gain intelligence, they should learn to find and process knowledge independently. Already in the early stages of theorizing about AI the problem of knowledge acquisition was considered. This problem focused on the transfer and transformation of potential problem solving expertise from a source to a program (Buchanan 1985). The challenge for the machine would be to determine the precise nature of the problem it needed to address. Next, it would have to query the available sources and to select the appropriate information. Finally, it would need to translate this information into an intelligible form by making use of its original programming. This task is made more difficult because of the complex, unstructured, often contradictory and generally unclearly formulated way in which human knowledge exists and is stored.

If these problems could ultimately be solved, machines would have to be able to independently construct a system that would allow them to organize and categorize the acquired information. This would involve that they create their own code and probably even an alternative to the way computers work today. Since all modern computers are essentially Turing-Machines, they suffer from the same limitations that are inherent to the way Turing-Machines function.

Existing examples of machines taking small steps into the direction that is described above are not very promising. Attempts to make machines produce their own original code (let alone develop an entirely new one) have resulted in copy-paste operations of existing codes (Reynolds n.d.).

For some time interlingual translation seemed to be a viable approach to the development of machine translation. Its principles are reminiscent of the approach that was proposed by René Descartes in the 17th century: essentially it involves the construction of an artificial intermediary language that allows basic linguistic concepts to be extracted from a given source-language and projected onto the target-language. In machine translation this concept has been adopted with some success, but it is has traditionally only been used for specific language pairs. Such a language, if it existed, would retain some elements of an ideal language in that it would be formally independent of the fuzziness of natural languages.

Sensational announcements have been made recently, claiming that the AI-group behind Google Translate had created such a language. Its interlingua was supposedly used as an intermediary language that could assist the translating of for example German into Mandarin Chinese (Wong 2016). This claim proved to be false (Reback 2017). In fact, most research into the use of an interlingua for machine translation has largely been abandoned. Google Translate and other projects have turned towards more promising approaches like Neural Machine Translation (NMT) (Zhang 2017).

It has been proposed (Johnson et al. 2016) to enhance Google’s neural machine translation system, so that it would be capable of translating between multiple language pairs using a single model. This would allow a machine to combine data from many known languages to translate to one target language. It could even be used to perform a so-called zero-shot translation, where the information of a multitude of known languages is used to translate a language, for which no previous data is available. This could be made possible by clustering semantically identical cross-language phrases. For example, by building a corpus of triplets out of phrases in English, Japanese and Korean that have the same underlying meaning and compiling them in a ground-truth database in one language, with which the other languages can be compared. Should this process be expanded and automated in a process involving self-learning machines, it is conceivable that a stable ground-truth database for the translation of all human languages could emerge. To this day, however, such advancements remain speculations with functioning applications only in science fiction (Lasbury 2017; Anonymous 2006).

[top of entry]

4.1.4 Formal concept analysis

Formal concept analysis (FCA) was formulated in the early 1980s by Rudolf Wille and can be considered a development of lattice theory (Wille 2009). Lattice theory was largely constructed in the nineteenth century as an attempt to formalise logic through the study of hierarchies. Its approach was based on a principle in traditional philosophy that states that a ‘concept’ is determined both by its ‘extent’ and its ‘intent’. Where the extent refers to all the object that belong to the same concept, the intent refers to all the attributes that are shared by those objects (Lambrechts 2012). Between different concepts there exists a natural hierarchy. A ‘triangle’ is for example a subset of the extent of ‘polygons’. This means that a triangle shares every attribute of a polygon, even though a triangle could have additional attributes. This works well enough for simple concepts, but problems quickly arise in situations where it is not possible to list all objects and their respective attributes, as it is generally the case in non-abstract situations. In those instances, the context for a fixed set of objects and attributes needs to be specified. FCA proposes a formalized method to establish and delineate any context. Priss (2006, 531) writes:

Formal concepts in FCA can be seen as a mathematical formalization of what has been called the “classical theory of concepts” in psychology/philosophy, which states that a concept is formally definable via its features. This theory has been refuted by Wittgenstein, Rosch (1973) and others but as Medin (1989, 1476) states: “despite the overwhelming evidence against the classical view, there is something about it that is intuitively compelling”. Even though from a psychological viewpoint the classical view does not accurately represent human cognition, the classical theory nevertheless dominates the design of computerized information systems because it is much easier to implement and to manage in an electronic environment. The classical view implicitly underlies many knowledge representation formalisms used in AI and in traditional information retrieval and library systems. Even if non-classical approaches are implemented (such as cluster analysis or neural networks), the resulting concepts are still sometimes represented in the classical manner.

It can be argued that by developing a formalised representation of the context, the system frees itself of that context. It does this by offering a method that aims to fit all conceivable concepts in a mathematical theory that does not require any further substantial theory. Such an undertaking can be considered to be a modern attempt to build an ideal language. And yet it is precisely this suggestion of independence from influences outside the mathematical sphere, that weakens the claim of FCA. It presupposes that concepts are somehow static in nature, whereas the opposite position has been upheld convincingly:

Concepts are dynamically constructed and collectively negotiated meanings that classify the world according to interests and theories. Concepts and their development cannot be understood in isolation from the interests and theories that motivated their construction, and, in general, we should expect competing conceptions and concepts to be at play in all domains at all times. (Hjørland 2009, 1522-3)

But these considerations did not diminish the potential FCA has for computer program design, in particular as a practical tool for context creation and formal concept mining [18].

[top of entry]

5. The linguistic turn

In parallel with the developments in logical positivism, a general reorientation of thinking about language took place that was later described as the linguistic turn in philosophy (Rorty 1992). Until then it had seemed that to shed light on what was being expressed in language, it was necessary to first find the underlying logical form. This approach involved two assumptions: one, that it was possible to extract an underlying logical form from language, and second, that this logical form was stable. But what if these things turned out to be unattainable?

A key figure in the linguistic turn within the English-speaking tradition is Ludwig Wittgenstein. Wittgenstein had been an inspirational figure for the Vienna Circle in the earlier stages of his thinking but became a prominent figure in this new movement during the second part of his life. In his Philosophical Investigations, he radically redefines the relation between meaning, context and language by defining the latter as an aggregate of language games:

Instead of producing something common to what we call language, I am saying that these phenomena [i.e. language games] have no one thing in common which makes us use the same word for all, but that they are related to one another in many different ways. And it is because of this relationship, or these relationships, that we call them all ‘language’. (Wittgenstein 1988, para. 65)

It is difficult to imagine an ideal language project that does not in some way reach out for an underlying layer of meaning that is common to all human beings, irrespectively of the language they speak. A tradition that started with the 18th century German poet and philosopher Johann Gottfried von Herder places a radically different perspective on language. For him all thought is dependent on and bounded by language (Forster 2011). This means that language is not merely a way through which we attempt to express common truths, but it is the source of our thoughts themselves. In this view, we are only able to think what our language allows us to express. When Friedrich von Schlegel builds on these Herderian thoughts, he adds that instead of seeing language as a contingent aggregation of words with different meanings, a language resembles an organism that follows a certain inner dynamism, and which is held together by a common grammar. According to this view the study of languages must focus mainly on their grammar. This allows for a method to be developed that would enable an empirical study of languages and map the genealogical relationship between different languages. In doing so, he finds that some languages exhibit this organic property more than others who display a more mechanical build-up [19].

Another thinker who was influenced by Herder concerning language theory was linguist and philosopher Wilhelm von Humboldt [20]. He agrees with Herder that it is our ability for language that gives humans their distinct awareness [21]. Words do not derive their meanings from timeless concepts, or Platonic ideas, but from the way in which they are used. One can see a great similarity between this view and what is suggested during the linguistic turn, over one hundred years later. From these assumptions, von Humboldt develops a program for the study of linguistics. A central idea here is that languages embody a diversity of worldviews and like with Schlegel he considers the study of grammar as fundamental for the investigation of languages. He expands Schlegel's two-fold interpretations (organic vs. mechanical) with an in-depth study of the grammatical properties of languages.

These insights have been extremely influential in the way modern language theory has formed. In a way, we may see the trajectory of finding a perfect formal language, beginning with Frege and ending with Wittgenstein and the "linguistic turn", as a failed detour from Herderian language theory. But what is equally true is that they leave little possibility, nor much desirability, to attain an ideal language. Within this tradition, the diversity in worldviews that comes with a diversity of languages is welcomed, not feared. It emphasises the merits of linguistic richness, instead of focussing on the lack of unity and the possibility of dissent that this diverse situation may cause between speakers of different languages.

Nonetheless, it does not necessarily follow from the apparent impossibility to reduce all languages to one ideal logical framework, that all rational basis for discourse is subsequently made impossible. The road towards a workable consensus of language and meaning may very well lie in adopting a form of pragmatism that is driven by a rational impetus. Possibly this consensus may come in the form of creating an ideal speech framework as was proposed by Jürgen Habermas (1970) or by instituting a programme of ‘transcendental semiotics’ as proposed by Karl-Otto Apel (1994).

[top of entry]

6. Conclusion

The subject of ideal language is an elusive one, in that it is both an oddity in the history of human ideas, consider for example the outlandishness of Llull’s system, and at the same time an all-encompassing project for human knowledge. In many respects it raises the stakes for what could be expected of formal knowledge systems and has certainly played a significant part in propelling the ambitions of Western thought towards new horizons.

Its ramifications span many fields and disciplines, ranging from linguistics to philosophy, science and mathematics, cognitive sciences, politics and theology. And even though the project, if indeed it can be called that, did not yet produce the outcomes it set for itself, it did generate several cultural and scientific products that were inspired by it. Among them diverse things ranging from Zermelo–Fraenkel set theory to universal human rights.

But what does this mean in terms of knowledge organization? Ideal languages aim to overcome the many deficiencies that are presumed to be present in natural languages, in particular the problem of ambiguity and lack of both stability and universal acceptance. To mend these problems the intention was not to construct a new and improved natural language, but to create a whole new rational model in which knowledge could be organised and communicated perfectly. And even though historically the attempts to create such a model often seemed to be motivated by a genuine social justification, the ambition of the ideal language project was to transcend its worldly context in the pursuit of universals.

In KOSs we see a similar ambition to provide a stable and universally accepted system that attempts to resolves the ambiguities of natural languages. The ambition, in the case of KOSs, is not to describe reality directly through the combination of eternal principles and questions (like in the case of Llull) or through the use of mathematical logic (like the logical positivists), but rather to organise and systematize all the knowledge that is already available. To achieve this goal however, KOSs themselves have come to appropriate all the distinguishing properties of an ideal language.

All key components that we identified for ideal languages in section 2.3 are also present in KOSs. Indeed, one could argue that the search for a perfect KOS shares more than just a common heritage with the search for an ideal language. Both are firmly rooted in a rationalist tradition, which believes in the possibility to develop a symbolic system that is able to claim perfect correspondence with the external world. And yet no KOS has ever described itself hyperbolically as a ‘mirror of nature’, or ‘the language of God’? What sets it apart from the most ambitious ideal language projects is its inherent intermediary character.

To clarify this distinction, let us again take the example of mathematical logic: At the height of the logical positivist movement, it was believed that all of nature could be described through logic. This meant that all the knowledge of the natural sciences of the time, who were already heavily reliant on mathematics, could be expressed in terms of mathematical logic. This translation would have been perfect. It would not lead to any loss of information and would achieve maximal clarity. In effect the ideal language called ‘logic’ would be able to completely replace the original formulations, their mathematical as well as their natural language form.

KOSs differ from what is described above in the sense that they must always be reliant on their subject matter to be meaningful. So even if they were able to perfectly describe any present or future knowledge, with just the combination of a limited set of facets for example, this description would not be able to completely replace the knowledge it organizes and describes. In so far a KOS can be considered an ideal language — ­­on account of the properties they share — it can only be one of a second order.

But herein lies a paradox: how can an ideal, and de facto a priori, language be reliant on information that is external to it? The inevitable answer is that it cannot. This implies that any KOS that asserts itself on these rationalist grounds is ultimately submitted to the same predicaments that have troubled all known ideal language projects.

These predicaments can be traced back to the refusal to let context or culture interfere with the inner workings of the ideal language, that finally undermined the project. By failing to overcome the constraints that present themselves in first order logical systems, no ideal language system can ever claim to be irrefutable. Considering that being self-explanatory is a necessary precondition for an ideal language to work in the first place, it seems that if there is no path available to circumvent these problems, the project has no hope of being revived in its original form.

But the ramifications of these findings stretch out even further and deal a significant blow to the rationalist worldview altogether. This raises the question whether KOSs should avoid a strictly rational approach as well? The story of the ideal language suggests that there is no such thing as a neutral logical system that could legitimize the development of an independent KOS for all present and future human knowledge. Any successful attempt to create a KOS therefore needs to be aware of these limits and must therefore be construed in accordance within a specific context and with a specific purpose in mind.

Ideal languages share a lot of common goals and principles with a KOS. But unlike a KOS, an ideal language is not merely an organizer of knowledge: It aims to constitute that knowledge. Rather than just being instrumental to a changing body of knowledge that is generated external to the system, as is the case in KOSs, an ideal language claims to produce new discoveries. As such, an ideal language is more like an axiomatic system in first order logic, capable of producing proofs, than to a KOS that is above all a practical tool.

Perhaps the most valuable by-product of the quest for an ideal language is the momentum it gave to the development of ever more efficient ways of organizing knowledge. The very idea that there must be a better, or even a perfect way to store, structure and convey meaningful information proved to be inspiring to many, even though the odds of ever finding such a perfect system are stacked against it.

[top of entry]

Endnotes

1. Ideal language is sometimes referred to as perfect language or even philosophical language. For the sake of clarity, we will limit ourselves to the term ideal language throughout this text. In addition to this, we chose to use the singular (ideal language) whenever the general concept of ideal language is addressed and the plural (ideal languages) when we refer to various actual historical attempts to create an ideal language. This decision is based on the logical assumption that no two languages can be ideal in equal measure.

2. Even though the view that natural languages are in some way deficient remains widespread, more recent approaches concerning this issue have suggested that there is a distinct functional relevance of polysemy (Temmerman 2000).

3. This rendering of Barons spectrum does not discuss other forms of symbolic representation known as constructed or a posteriori languages as, such as music notation or specific scientific notations as they are used for example in physics, chemistry or biology.

4. More on the subject of artificial languages, in particular about Francis Bacon, Samuel Hartlib and John Webster can be found in Lewis (2007).

5. ‘Je ne sais pas pourquoi il est dit dans la Genèse que Babel signifie confusion, car Ba signifie Père dans les langues Orientales, & Bel signifie Dieu, Babel signifie la ville de Dieu, la ville Sainte. Les anciens donnaient ce nom à toutes leurs capitales. Mais il est incontestable que Babel veut dire confusion, soit parce que les Architectes furent confondus après avoir élevé leur ouvrage jusqu’à quatre-vingt & une mille pieds Juifs, soit parceque les langues se confondirent, & c’est évidemment depuis ce tems-là que les Allemands n’entendent plus les Chinois ; car il est clair, selon le savant Bauchard, que le Chinois est originairement la même langue que le haut Allemand.’ (Voltaire 2005)

6. Note that Voltaire's etymology is incorrect from a modern linguistic perspective (though he could not have known this in his time): Babel akk. Bab ili "Gate of God".

7. The notion of a scale of being can be linked to the concept of integrative levels, through the analysis of the scale of complexity and organisation of a given subject. For further elucidation on this topic read Kleineberg (2017).

8. Marin Mersenne (1588-1648) was a clergyman, mathematician and theologian, involved in the strict ascetical order of the Fratres Minores. His cell in Paris was intensely visited by leading intellectuals from his time, like Pascal and Fermat.

9. George Dalgarno (1616-1687) is not discussed in full in this text. As a scholar he was part of the nucleus of the Royal Society, together with John Wilkins. Dalgarno had worked on a new system for writing shorthand. Together with Wilkins he would further develop the 'real character' into a philosophical language based on rational principles. More about him is to be found in Maat (2001).

10. For example: the set of factorials for the number 81374 in the example are {2, 23, 29, 61}, so the complexity of the expression would be of a level four.

11. As mentioned earlier, the movement of logical positivism did not have a social or political agenda, but that did not mean that its members were safe from prosecution by proponents of a conflicting ideology. Founder Moritz Schlick was murdered on the steps of the university where he taught, and most of the members of the circle had to flee the European mainland in the 1930s for fear of prosecution.

12. Russell's paradox is a classic problem in set-theory. Put into a simple form, it can be expressed as follows:
‘Some sets, such as the set of all teacups, are not members of themselves. Other sets, such as the set of all non-teacups, are members of themselves. Call the set of all sets that are not members of themselves R. If R is a member of itself, then by definition it must not be a member of itself. Similarly, if R is not a member of itself, then by definition it must be a member of itself’ (Irvine and Deutsch 2016).

13. This is an example of the liar paradox, a standard paradox involving self-reference. To grasp its meaning, one may consider for example a liar sentence like ‘What is written here is not true’ and call it L. The paradoxical nature of this expression can be coined as follows:
‘Let L be the Classical Liar Sentence. If L is true, then L is false. But we can also establish the converse, as follows. Assume L is false. Because the Liar Sentence is just the sentence that 'says' L is false, the Liar Sentence is therefore true, so L is true. We have now shown that L is true if, and only if, it is false. Since L must be one or the other, it is both.’ (Dowden 2017)

14. For a comprehensive overview of Gödel's theorem we recommend "Gödel's theorem: an incomplete guide to its use and abuse" by Torkel Franzén (Franzén 2005).

15. At the very least, Gödel's theorem was a major blow to the program of David Hilbert who wanted to formalize all of mathematics in axiomatic form, together with the proof that this axiomatization of mathematics is consistent.

16. Consider for example a program that instructs the computer to just add 1 to a given number and repeat this operation with the result.

17. The proof that Turing delivered is complex, but it can be summarized as follows:
Consider a program halt(A,x) that results in a 1 if the algorithm A finishes in a finite number of steps given input x, and in 0 if, this is not the case and the algorithm goes on indefinitely.
Now think of the algorithm paradox(A), that actually gives a value (any value), when halt(A,A) results in 0, and goes on indefinitely, if halt(A,A) results in 1.
Now consider what happens, when paradox gets paradox as its input. Does it end?
If it does, then halt(paradox, paradox) should result in 0. But according to the definition of halt, this would mean that the paradox does not end.
If it does not, then halt(paradox, paradox) should result in 1. But, again according to the definition, a 1 means that the program would end.
So paradox(paradox) can in fact not end. This is of course incongruous with the first principle.

18. For an overview of available software that uses the FCA framework, go to http://www.upriss.org.uk/fca/fcasoftware.html

19. Frederich von Schlegel found that 'organic' languages (like Sanskrit, Persian and the European languages) where essentially comprised of roots and additional elements marking gender, number, tense etc. A grammatical technique he called "Flexion". These organic languages where supposedly superior to 'mechanical' languages (like Chinese, Coptic and Arabic) that showed elements that where connected more loosely to the word roots, which he called "Affixa". Because of this, mechanical languages were said to be less able to deal with external influences. Organic languages, on the other hand, would be able to absorb additional information that was given to them by historic forces due to their greater flexibility. This principle would give organic languages a greater richness. (Errington 2008)

20. He was the older brother of the better known omnivorus intellectual Alexander von Humboldt.

21. This take on language has later been known as the "Sapir-Whorf hypothesis" i.e. roughly, the hypothesis that the different characters of different languages produce different types of thought/conceptualisation (Evans and Foster 2011).

[top of entry]

References

Anonymous. 2006. "How to Build a Babel Fish". The Economist Technology Quarterly 379, June: 1–4.

Apel, Karl-Otto. 1994. "Towards a Transcendental Semiotics". In Selected Essays, Vol. 1. New York: Humanities Press.

Baron, Naomi S. 1994. "Computer Languages". Encyclopedia of Language & Linguistics. Oxford: Pergamon Press, Vol. 2: 662-670.

Bawden, David. 2017. "Chemistry and Its (Information) History". https://theoccasionalinformationist.com/2017/09/03/chemistry-and-its-information-history/. Accessed: February 28, 2018.

Bergman, Mike. 2007. "An Intrepid Guide to Ontologies". AI3. http://www.mkbergman.com/wp-content/uploads/kalins-pdf/singles/374.pdf. Accessed: February 28, 2018.

Bloch, Bernard, and George Leonard Trager. 1942. Outline of Linguistic Analysis. Baltimore?: Published by Linguistic Society of America at the Waverly Press.

Bonner, Anthony. 2007a. The Art and Logic of Ramon Llull: A User’s Guide. Leiden: BRILL.

Bonner, Anthony. 2007b. "What Was Llull up To?" Brazilian Institute of Philosophy and Science Raimundo Lúlio. Available at http://www.ramonllull.net/sw_studies/studies_original/compbon.html. Accessed: February 28, 2018.

Borges, Jorge Luis. 1988. "The Analytical Language of John Wilkins". In Other Inquisitions 1937-1952. London: Souvenir Press: 101-105

Buchanan, Bruce G. 1985. Some Approaches to Knowledge Acquisition. Stanford: Stanford University, Department of Computer Science. (Knowledge Systems Laboratory Report No. KSL-85-38), also available at https://pdfs.semanticscholar.org/7874/4a31e702c78e373f311bb814cc245a1a7f62.pdf

Chomsky, Noam. 1957. Syntactic Structures. The Hague: Mouton.

Clauss, Sidonie. 1982. "John Wilkins’ Essay Toward a Real Character?: Its Place in the Seventeenth-Century Episteme". Journal of the History of Ideas 43, no 4: 531–53.

Cooper, S. Barry. 2012. "Incomputability after Alan Turing". Notices of the American Mathematical Society 59, no 6: 776–84. doi:10.1090/noti866.

Dante Alighieri. 1996. De vulgari eloquentia. Edited by Steven Botterill. Cambridge: Cambridge University Press. https://www.danteonline.it/english/opere.asp?idope=3&idlang=UK.

Derrida, Jacques. 1985. "Des Tours de Babel”. In Difference in Translation. Ithaca: Cornel University Press: 165-248

Descartes, René. 2017. Selected Correspondence of Descartes. By Jonathan Bennett. First launched: April 2013. http://www.earlymoderntexts.com/assets/pdfs/descartes1619_1.pdf.

Eco, Umberto. 1995. The Search for the Perfect Language. Oxford: Blackwell.

Emery, Clark. 1948. “John Wilkins’ Universal Language”. Isis 38, nos 3/4: 174–85.

Errington, Joseph. 2008. Linguistics in a Colonial World?: A Story of Language, Meaning, and Power. Malden: Blackwell.

Evans, James A, and Jacob G Foster. 2011. “Metaknowledge”. Science 331, edition february: 721–25.

Fodor, Jerry Alan. 1978. The Language of Thought. Hassocks: Harvester press.

Forster, Michael N. 2011. German Philosophy of Language from Schlegel to Hegel and Beyond. Oxford: Oxford University Press.

Foskett, Douglas J. 1980. “Thesaurus”. Encyclopedia of Library and Information Science. Edited by Allen Kent. New York: Marcel Dekker, Vol. 30: 416-63.

Genesis n.d. 11:9. Available at https://www.biblegateway.com/passage/?search=Genesis+11:1-9.

Gracia, Jorge, and Lloyd Newton. 2016. “Medieval Theories of the Categories”. The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/win2016/entries/medieval-categories/.

Gruber, Thomas R. 1993. “A Translation Approach to Portable Ontology Specifications”. Knowledge Acquisition 5, no 2: 199–220.

Habermas, Jürgen. 1970. “Towards a Theory of Communicative Competence”. Inquiry: An Interdisciplinary Journal of Philosophy 13, nos 1–4: 360–75.

Hauser, Marc D., and Jeffrey Watumull. 2016. “The Universal Generative Faculty: The Source of Our Expressive Power in Language, Mathematics, Morality, and Music”. Journal of Neurolinguistics 43, Part B: 78-94.

Hillgarth, J.N. 1971. Ramon Lull and Lullism in Fourteenth-Century France. Oxford: Oxford University Press.

Hjørland, Birger. 2008. “What Is Knowledge Organization (KO)?” Knowledge Organization 35, nos 2/3: 86–101.

Hjørland, Birger. 2009. “Concept Theory”. Journal of the American Society for Information Science and Technology 60, no 8: 1519–36.

Hjørland, Birger. 2013. "Facet Analysis: The Logical Approach to Knowledge Organization". Information Processing & Management Vol. 49: 545–557.

Hjørland, Birger 2015. “Are Relations in Thesauri ‘Context-Free, Definitional, and True in All Possible Worlds’?” Journal of the Association for Information Science and Technology 66, no 7: 1367–73.

Hjørland, Birger. 2016. “Knowledge Organization (KO)”. Knowledge Organization 43, no 7: 475–84. Also available in Hjørland, Birger, ed. ISKO Encyclopedia of Knowledge Organization, http://www.isko.org/cyclo/knowledge_organization.

Hjørland, Birger. 2017. “Classification”. Knowledge Organization 44, no. 2: 97-128. Also available in Hjørland, Birger, ed. ISKO Encyclopedia of Knowledge Organization, http://www.isko.org/cyclo/classification

Hofweber, Thomas. 2017. “Logic and Ontology”. The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/logic-ontology/.

Irvine, Andrew David, and Harry Deutsch. 2016. “Russell’s Paradox”. The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/win2016/entries/russell-paradox/.

Johnson, Melvin, Mike Schuster, Quoc V. Le, Maxim Krikun, Yonghui Wu, Zhifeng Chen, Nikhil Thorat, et al. 2017. “Google’s Multilingual Neural Machine Translation System: Enabling Zero-Shot Translation” Transactions of the Association for Computational Linguistics s, vol. 5: 339–351

Katz, Matthew. 2017. “The Language of Thought Hypotesis”. Internet Encyclopedia of Philosophy. Available at http://www.iep.utm.edu/lot-hypo/#H1.

Kennedy, Hubert. 2002. “Peano — The Unique”. In Twelve Articles on Giuseppe Peano, 107. San Francisco: Peremptory Publications.

Kirkham, Richard L. 1992. Theories of Truth?: A Critical Introduction. London: MIT press.

Kleineberg, Michael. 2017. “Integrative Levels”. Knowledge Organization 44, no 5: 349–79. Also available in Hjørland, Birger, ed. ISKO Encyclopedia of Knowledge Organization, http://www.isko.org/cyclo/integrative_levels

Knuth, Donald E. 2006. The Art of Computer Programming: Generating All Trees. Boston: Addison-Wesley Professional.

Lambrechts, Lieve. 2012. Formal Concept Analysis. Dissertation, Vrije Universiteit Brussel.

Lasbury, Mark E. 2017. “The Realization of Star Trek Technologies”. In The Realization of Star Trek Technologies. Berlin: Springer.

Leibniz, Gottfried Wilhelm. 1666. “Dissertatio de Arte Combinatoria”. Edition from the collection of the Biblioteca Nazionale Centrale di Firenze. Available at https://archive.org/details/ita-bnc-mag-00000844-001.

Lenzen, Wolfgang. 2017. “Leibniz: Logic”. Internet Encyclopedia of Philosophy. Available at http://www.iep.utm.edu/leib-log/#SH2b.

Lewis, Rhodri. 2007. Language, Mind and Nature: Artificial Languages in England from Bacon to Locke. Cambridge: Cambridge University Press.

Lima, Manuel. 2011. Visual Complexity: Mapping Patterns of Information. Princeton: Princeton Architectural Press.

Llull, Ramon. 1635. Arbor Scientiae. Edited by François Plaignard and Caffin Jean. ex officina Ioannis Pillehotte. Available at https://books.google.be/books?id=I64oL87aiS0C&hl=nl&pg=PP7#v=onepage&q&f=false.

Llull, Ramon. 1970. Ars Generalis Ultima. Frankfurt: Minerva-Verlag.

Lyons, John. 1977. Semantics, Volume I. Cambridge; London: Cambridge University Press.

Maat, David Cram and Jaap. 2001. George Dalgarno on Universal Language: The Art of Signs (1661), The Deaf and Dumb Man’s Tutor (1680), and the Unpublished Papers. Edited by David Cram and Jaap Maat. Oxford: Oxford University Press.

Mazzocchi, Fulvio. 2013. "Images of Thought and Their Relation to Classification: The Tree and the Net". Knowledge Organization. Vol. 40.

Medin, Douglas L. 1989. “Concepts and Conceptual Structure”. American Psychologist 44, no 12: 1469–81.

Miksa, Francis L. 1998. The DDC, the Universe of Knowledge, and the Post-Modern Library. Albany, N.Y.: Forest Press.

Mooers, Calvin N. 1985. “The Indexing Language of an Information Retrieval System”. In Theory of Subject Analysis, 247–61. Littleton: Libraries Unlimited.

Priss, Uta 2006. “Formal Concept Analysis in Information Science”. Annual Review of Information Science and Technology 40, no 1: 521–43.

Ranganathan, Shiyali Ramamrita. 1989. Philosophy of Library Classification. Bangalore: Sarada Ranganathan Endowment for Library Science. Available at http://arizona.openrepository.com/arizona/handle/10150/105278#.

Ranganathan, Shiyali Ramamrita. 1990. A Descriptive Account of the Colon Classification. Bangalore: Sarada Ranganathan Endowment for Library Science.

Reback, Gedalyah. 2017. “No, Google Translate Did Not Invent Its Own Language Called ‘interlingua.’” Geektime. Available at http://www.geektime.com/2017/01/23/no-google-translate-did-not-invent-its-own-language-called-interlingua/.

Reynolds, Matt. 2017. “AI Learns to Write Its Own Code by Stealing from Other Programs”. New Scientist. News & Technology 22 February 2017 . Available at https://www.newscientist.com/article/mg23331144-500-ai-learns-to-write-its-own-code-by-stealing-from-other-programs/.

Richardson, J. S. 1991. “Imperium Romanum?: Empire and the Language of Power”. The Journal of Roman Studies 81: 1–9.

Rorty, Richard. 1992. The Linguistic Turn?: Essays in Philosophical Method. Chicago (Ill.): University of Chicago press.

Rosch, Eleanor. 1973. “Natural Categories”. Cognitive Psychology 4: 328–50.

Roget, Peter Mark. 1805/1852. Thesaurus of English Words and Phrases, Classified and Arranged so as to Facilitate the Expression of Ideas and Assist in Literary Composition. London: Longman, Brown, Green, and Longmans. (Manuscript finished 1805).

Russell, Bertrand. 1919. “The Philosophy of Logical Atomism”. The Monist 29, no 3: 345–80.

Sapir, Edward. 1921. Language: An Introduction to the Study of Speech. New York: Harcourt, Brace and company.

Schulte-Albert, H. G. 1974. “Cyprian Kinner and the Idea of a Faceted Classification“. Libri 24, no 4: 324–337.

Smith, Barry. 2004. “Beyond Concepts?: Ontology as Reality Representation”. In Proceedings of FOIS 2004, 4–6. http://ontology.buffalo.edu/bfo/BeyondConcepts.pdf.

Smokotin, Vladimir M., and Galina I. Petrova. 2015. “The Quest for a Universal Language throughout Human History”. Procedia — Social and Behavioral Sciences 200, October: 107–13.

Speer, Rob, and Catherine Havasi. 2004. “Meeting the Computer Halfway?: Language Processing in the Artificial Language Lojban”. Proceedings of MIT Student Oxygen Conference. Massachusetts Institute of Technology.

Stria, Ida. 2016. Inventing Languages, Inventing Worlds. Poznan: Wydzial Neofilologii UAM.

Svenonius, Elaine. 2004. “The Epistemological Foundations of Knowledge Representations”. Library Trends 52, no 3: 571–87.

Tang, Yanfang. 1999. “Language , Truth , and Literary Interpretation?: A Cross-Cultural Examination”. Journal of the History of Ideas 60, no 1: 1–20.

Temmerman, Rita. 2000. Towards New Ways of Terminology Description: The Sociocognitive-Approach. Amsterdam: Benjamins.

Turing, A. M. 1938. “On Computable Numbers, with an Application to the Entscheidungsproblem: a Correction”. Proceedings of the London Mathematical Society s2-43, no 1: 544–46.

Van Parijs, Philippe. 2004. “Europe’s Linguistic Challenge”. Archives Européennes de Sociologie 45, no 1: 113–54.

Voltaire. 1901. “Babel”. A Philosophical Dictionary, Volume 02. E.R. DuMont. Available at http://www.gutenberg.org/files/35622/35622-h/35622-h.htm.

Voltaire. 2005. Dictionnaire philosophique. Almeria: Le chasseur abstrait.

Walker, Thoman D. 1996. “Medieval Faceted Knowledge Classification: Ramon Llull’s Trees of Science”. Knowledge Organization 23, no 4: 199–205.

Weiten, Wayne. 2013. Psychology: Themes and Variations. London: Wadsworth.

Whitley, Richard R. 1984. The Intellectual and Social Organization of the Sciences. Oxford: Oxford University Press.

Wilkins, John. 1668. An Essay towards a Real Character and a Philosophical Language. London: Royal Society. Available at https://archive.org/details/AnEssayTowardsARealCharacterAndAPhilosophicalLanguage.

Wille, Rudolf. 2009. “Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts”. In: Ferre, Sebastien, Rudolph, Sebastian (Eds.), Formal Concept Analysis: 7th International Conference, ICFCA 2009 Darmstadt, Germany, May 21-24, 2009. Springer, chapter 23: 314-39.

Wittgenstein, Ludwig. 1988. Philosophical Investigations. Oxford: Blackwell.

Wong, Sam. 2016. “Google Translate AI Invents Its Own Language to Translate with”. New Scientist. Available at https://www.newscientist.com/article/2114748-google-translate-ai-invents-its-own-language-to-translate-with/

Zach, Richard. 2007. “Hilbert’s Program Then and Now”. Philosophy of Logic 9: 411–47.

Zeng, Marcia Lei. 2008. “Knowledge Organization Systems (KOS)”. Knowledge Organization 35, no 2: 160–82.

Zhang, Mos. 2017. “History and Frontier of the Neural Machine Translation”. Medium. https://medium.com/@Synced/history-and-frontier-of-the-neural-machine-translation-dc981d25422d. Accessed on February 28, 2018.

[top of entry]

Visited times since 2018-03-14.

Version 1.1 (= 1.0 plus reference to Schulte-Albert 1974); version 1.0 published 2018-03-20, this version 2018-10-31, last edited 2018-10-31
Article category: Methods, approaches and philosophies

This article (version 1.0) is published in Knowledge Organization, vol. 45 (2018), Issue 7, pp. 586-608.
How to cite it (version 1.0): Laporte, Steven. 2018. “Ideal language”. Knowledge Organization 45, no. 7: 586-608. Also available in ISKO Encyclopedia of Knowledge Organization, ed. Birger Hjørland, coed. Claudio Gnoli, http://www.isko.org/cyclo/ideal_language

©2018 ISKO. All rights reserved.